
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

В результате получаем общее решение системы
|
|
 .
.
Одно базисное решение получаем при 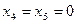 , т.е.
, т.е. 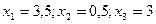 или
или 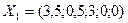 .
.
Чтобы получить другое базисное решение, достаточно задать 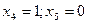 , тогда
, тогда 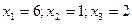 или
или 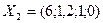 .
.
Пример 6. Даны векторы 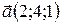 ,
, 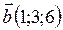 ,
, 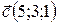 ,
, 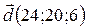 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы  ,
,  ,
, 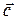 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 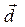 в этом базисе.
в этом базисе.
Решение:
Для того, чтобы три вектора могли образовывать базис пространства 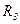 , необходимо и достаточно, чтобы они были линейно независимы. Это значит, определитель, столбцами которого являются координаты векторов системы, должен быть отличен от нуля.
, необходимо и достаточно, чтобы они были линейно независимы. Это значит, определитель, столбцами которого являются координаты векторов системы, должен быть отличен от нуля.
Вычислим определитель  системы.
системы.
 .
.
Вывод: векторы 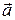 ,
, 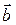 ,
, 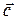 линейно независимы и образуют базис в
линейно независимы и образуют базис в 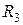 .
.
Разложение вектора 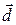 по базису
по базису 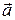 ,
, 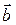 ,
, 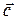 в векторной форме имеет вид:
в векторной форме имеет вид:
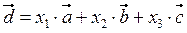 ,
,
где х1, х2, х3 – искомые координаты вектора 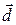 в данном базисе.
в данном базисе.
В координатной форме это разложение имеет вид:
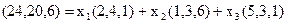
или
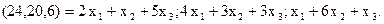
В левой и правой частях полученного равенства стоят два вектора. Они равны и поэтому равны их одноименные координаты. Получим систему трех уравнений с тремя неизвестными:
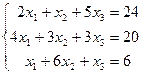 .
.
Систему решаем по формулам Крамера. Для этого, кроме определителя  , вычисляем
, вычисляем 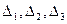 полученные из определителя
полученные из определителя  заменой соответствующих столбцов столбцом свободных членов системы.
заменой соответствующих столбцов столбцом свободных членов системы.
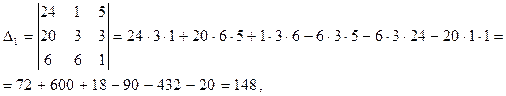
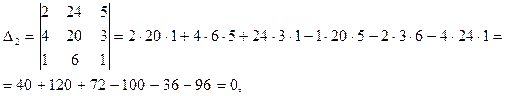
Координаты вектора 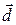 определяются по формулам:
определяются по формулам:
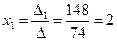 ;
; 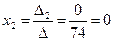 ;
; 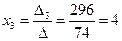 .
.
Таким образом, разложение вектора 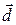 по базису
по базису 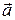 ,
, 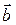 ,
, 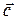 имеет вид:
имеет вид: 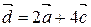 или
или 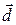 (2; 0; 4).
(2; 0; 4).
Проверка. Подставим в правую часть полученного разложения координаты векторов 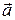 ,
, 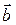 ,
, 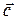 :
:
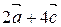 = 2 (2; 4; 1)+ 4 (5; 3; 1;)=(4; 8; 2)+(20; 12; 4)=(24; 20; 6)=
= 2 (2; 4; 1)+ 4 (5; 3; 1;)=(4; 8; 2)+(20; 12; 4)=(24; 20; 6)= 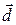 .
.
Получили координаты вектора 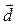 . Значит, разложение вектора
. Значит, разложение вектора 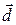 по базису
по базису 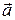 ,
, 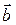 ,
, 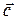 найдено верно.
найдено верно.
Пример 7. Даны координаты вершин пирамиды ABCD: A(10;6;6), B(−2;8;2), C(6;8;9), D(7;10;3).
Найти:
1) Длину ребра АВ;
2) Угол между ребрами АВ и АD;
3) Уравнение прямой АВ;
4) Уравнение плоскости АВС;
5) Угол между ребром АD и гранью АВС;
6) Площадь грани АВС;
7) Объем пирамиды;
8) Уравнение высоты, опущенной из вершины D на грань АВС.
Сделать чертеж.
Решение:
1) Если ребро АВ обозначить за вектор 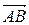 , то длина ребра − это длина вектора. Находим координаты вектора
, то длина ребра − это длина вектора. Находим координаты вектора 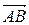 :
:
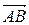 =(− 2−10; 8−6; 2−6)=(− 12; 2;− 4).
=(− 2−10; 8−6; 2−6)=(− 12; 2;− 4).
Если 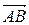 =(х; у: z), то его длина
=(х; у: z), то его длина 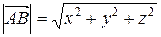 .
.
Следовательно,
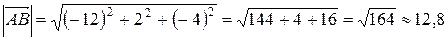 .
.
2) Угол между ребрами АВ и АD – это угол между векторами 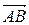 и
и 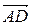 . Находим координаты вектора
. Находим координаты вектора 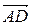 .
.
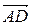 =(7−10; 10−6;3−6)=(−3;4;−3).
=(7−10; 10−6;3−6)=(−3;4;−3).
Из пункта 1) нам известны координаты вектора 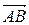 =(− 12; 2;− 4). Угол между двумя векторами находится по формуле:
=(− 12; 2;− 4). Угол между двумя векторами находится по формуле:
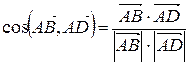 .
.
Если векторы 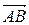 и
и 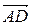 имеют координаты
имеют координаты 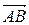 =(х1; у1: z1),
=(х1; у1: z1), 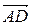 (х2; у2: z2) соответственно, то эта формула перепишется в виде:
(х2; у2: z2) соответственно, то эта формула перепишется в виде:
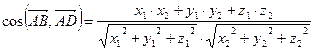 .
.
Следовательно, получаем
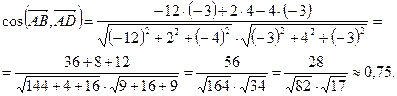
Итак,  .
.
3) Уравнение прямой, проходящей через две точки М1(х1;у1;z1) и М2(х2;у2;z2) имеет вид:
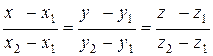

или равносильное ему уравнение:
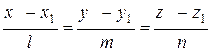 ,
,
где 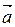 =(l,m,n) – координаты направляющего вектора прямой М1М2.
=(l,m,n) – координаты направляющего вектора прямой М1М2.
Направляющий вектор прямой – это вектор, параллельный прямой. В нашем случае прямая проходит через точки А(10;6;6) и В(−2;8;2). Следовательно, уравнение прямой АВ:
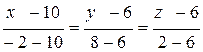 .
.
Итак, каноническое уравнение прямой АВ:
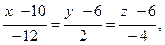
где направляющий вектор

4) Уравнение плоскости по трем точкам находится по формуле:
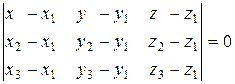 , (*)
, (*)
где А(х1;у1;z1); В (х2;у2;z2); С(х3;у3;z3) – точки, через которые проходит плоскость. Подставляя координаты точек А, В, С в формулу (*), получим:
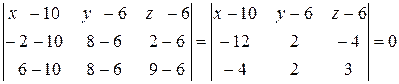 .
.
Считаем определитель, разложив его по первой строке.
D=а11А11+а12А12+а13А13,
где  − алгебраические дополнения элементов
− алгебраические дополнения элементов 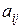 , а Мi j – минор элемента
, а Мi j – минор элемента 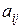 . Минором элемента матрицы называется определитель, получаемый (вычеркиванием строки и столбца, на пересечении которых он расположен) из данного. Следовательно,
. Минором элемента матрицы называется определитель, получаемый (вычеркиванием строки и столбца, на пересечении которых он расположен) из данного. Следовательно,
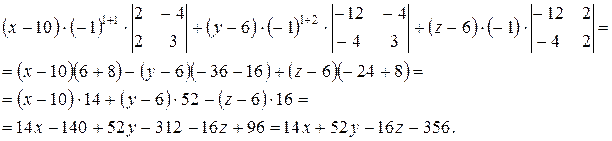
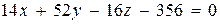 .
.
Итак, уравнение плоскости АВС:
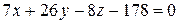 .
.
5) Требуется найти угол между ребром АD и гранью АВС. Это равносильно нахождению угла между прямой АD и плоскостью АВС. Угол между прямой 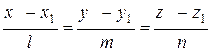 и плоскостью Ах+Ву+Сz+D=0 определяется по формуле:
и плоскостью Ах+Ву+Сz+D=0 определяется по формуле:
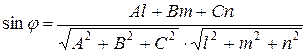 ,
,
где 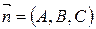 − координаты нормального вектора плоскости АВС.
− координаты нормального вектора плоскости АВС.
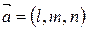 − координаты направляющего вектора прямой АD.
− координаты направляющего вектора прямой АD.
Находим уравнение прямой АD по двум точкам:
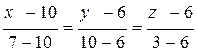 .
.
Следовательно,
АD: 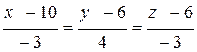 ,
, 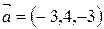 .
.
Т.к. уравнение плоскости АВС: 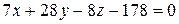 , то ее нормальный вектор
, то ее нормальный вектор  .
.
Значит,
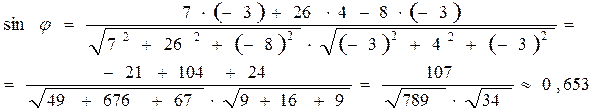 .
.
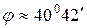 .
.
6) Площадь грани АВС – это площадь треугольника АВС. Если треугольник построен на векторах 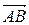 и
и  , то его площадь считается по формуле:
, то его площадь считается по формуле:
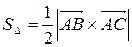 .
.
Из пункта 1) имеем 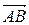 =(− 12; 2;− 4).Находим координаты вектора
=(− 12; 2;− 4).Находим координаты вектора  .
.
 =(6−10;8−6;9−6)=(−4;2;3).
=(6−10;8−6;9−6)=(−4;2;3).
Далее необходимо найти векторное произведение 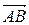
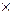
 .Составляем определитель и вычисляем его, раскладывая по первой строке.
.Составляем определитель и вычисляем его, раскладывая по первой строке.
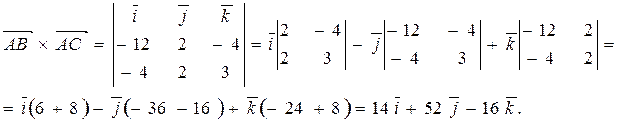
находим длину полученного вектора:
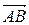
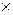

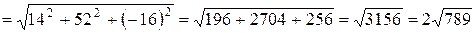 .
.
Следовательно,
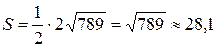 .
.
7) Объем пирамиды равен 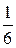 объема параллелепипеда, построенного на векторах
объема параллелепипеда, построенного на векторах 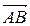 ,
,  ,
, 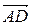 . Координаты этих векторов найдены ранее:
. Координаты этих векторов найдены ранее: 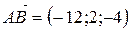 ,
, 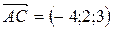 ,
, 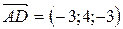 .
. 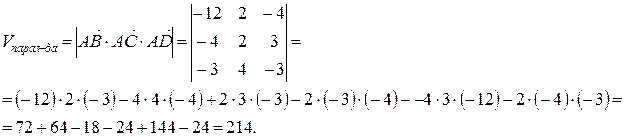
Следовательно, 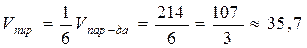 .
.
8) Грань АВС имеет нормальный вектор 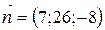 . Для того, чтобы составить уравнение высоты, надо знать направляющий вектор
. Для того, чтобы составить уравнение высоты, надо знать направляющий вектор  той прямой, где лежит высота. Т.к. DH^ABC (DH −высота), то
той прямой, где лежит высота. Т.к. DH^ABC (DH −высота), то 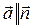 (
(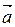 −параллелен прямой DH, а
−параллелен прямой DH, а 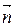 − перпендикулярен АВС). Следовательно, в качестве направляющего вектора прямой DH можно взять нормальный вектор плоскости АВС. Т.е.
− перпендикулярен АВС). Следовательно, в качестве направляющего вектора прямой DH можно взять нормальный вектор плоскости АВС. Т.е. 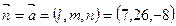 . Уравнение высоты имеет вид:
. Уравнение высоты имеет вид:
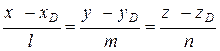 .
.
Итак, получили уравнение высоты DH:
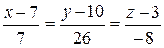 .
.
Пример 8. Даны вершины треугольника А(1;−1), В(−2;−6), С(−6;3). Требуется: 1) вычислить длину высоты и медианы, проведенной из вершины В; написать их уравнения; 2) написать уравнения прямой, проходящей через вершину В параллельно стороне АС; 3) найти угол между прямыми АВ и АС; 4) найти точку В1 симметричную точке В относительно прямой АС.
Решение:
1.а) Составим уравнение медианы, проведенной из вершины В. Пусть М – середина АС. Найдем её координаты:
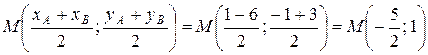 .
.
Уравнение прямой по двум точкам находится по формуле:
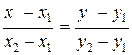 .
.
BМ: 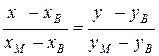 Þ
Þ 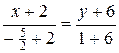 Þ
Þ 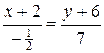 .
.
Приведем это уравнение к общему виду прямой.
−14(х +2) = у +6 Þ −1 4х − 28 = у +6 Þ ВМ: 14х+у+34=0.
(Общий вид прямой А х + В у+С=0).
Длину медианы ВМ вычисляем по формуле: 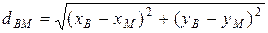 .
.
Тогда 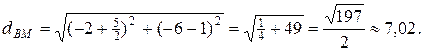
1.б) Составим уравнение стороны АС – основания высоты ВН по известным двум точкам
АС: 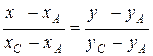 Þ
Þ 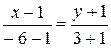 Þ
Þ 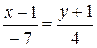 .
.
Приведем это уравнение к общему виду прямой.
4(х −1) = −7(у +1) Þ 4х − 4 = −7 у −7 Þ АС: 4х+7у+3=0.
Угловой коэффициент этой прямой 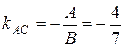 . Две прямые перпендикулярны, если:
. Две прямые перпендикулярны, если: 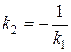 . Т. к. АС ^ ВН, то
. Т. к. АС ^ ВН, то 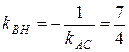 .
.
Составим уравнение высоты ВН, зная, ее угловой коэффициент и точку В.
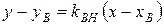 .
.
 Þ 4 (у+6)=7(х+2) Þ 4 у+24=7х+14.
Þ 4 (у+6)=7(х+2) Þ 4 у+24=7х+14.
ВН: 7х−4у−10=0.
Вычислим длину высоты ВН, как расстояние от точки В до прямой АС, по формуле  . Тогда получим
. Тогда получим
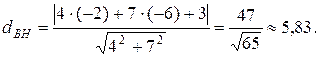
2) Известно, что если прямые параллельны, то их угловые коэффициенты совпадают. Следовательно, т. к BL|| AC,то 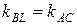 .
.
Составляем уравнение прямой BL, зная ее угловой коэффициент 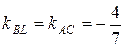 и точку B(−2;−6), через которую проходит эта прямая, т. е.
и точку B(−2;−6), через которую проходит эта прямая, т. е.
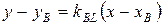 .
.
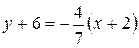 Þ7 у+42=−4х−8 Þ BL: 4х+7у+50=0.
Þ7 у+42=−4х−8 Þ BL: 4х+7у+50=0.
3) Найдем угол между прямыми АВ и АС. Составим уравнение прямой АВ по известным двум точкам
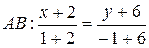 Þ
Þ 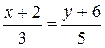 . 5(х +2) = 3(у +6) Þ 5 х+10 = 3 у +18 Þ АВ: 5х−3у−8=0.
. 5(х +2) = 3(у +6) Þ 5 х+10 = 3 у +18 Þ АВ: 5х−3у−8=0.
Угловой коэффициент АВ: 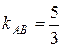 . Знаем, что
. Знаем, что 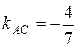 .
.
Воспользуемся формулой
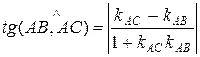 .
.
Для данного случая
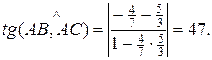
 .
.
4) Из п.1.б) известны уравнения стороны АС: 4х+7у+3=0 и высоты ВН: 7х−4у−10=0. Найдем точку их пересечения:
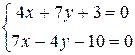
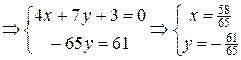 .
.
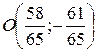 − точка пересечения стороны АС и высоты ВН. Эта же точка является серединой отрезка ВВ1. Зная формулы координат середины отрезка
− точка пересечения стороны АС и высоты ВН. Эта же точка является серединой отрезка ВВ1. Зная формулы координат середины отрезка
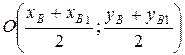 ,
,
выведем формулы 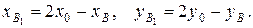
Для данного случая получаем: 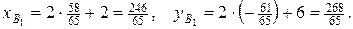 Окончательно имеем:
Окончательно имеем: 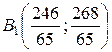 .
.
Пример 9. Линия, заданная уравнением r=r(j) в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от j=0 до j=2p и придавая j значения через промежуток 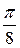 ;
;
2) найти уравнение данной линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью;
3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия:
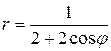 .
.
Решение:
1) Рассмотрим первый способ построения кривой. Придавая углу значения через промежуток 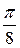 , вычисляем соответствующие значения, радиуса r и записываем в виде таблицы, найденные полярные координаты точек.
, вычисляем соответствующие значения, радиуса r и записываем в виде таблицы, найденные полярные координаты точек.
| j | 0 | 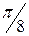
| 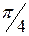
| 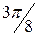
| 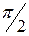
| 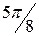
| 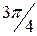
| 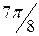
| p | ||||||||
| r | 0,25 | 0,26 | 0,29 | 0,36 | 0,5 | 0,81 | 1,71 | 6,57 | ¥ | ||||||||
| j | 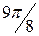
| 
| 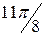
| 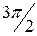
| 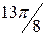
| 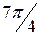
| 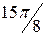
| 2p | |||||||||
| r | 6,57 | 1,71 | 0,81 | 0,5 | 0,36 | 0,29 | 0,26 | 0,25 | |||||||||
По найденным точкам строим кривую в полярной системе координат (см. рис.1.)
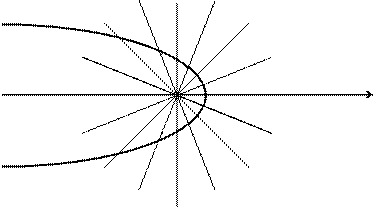 |
Рис.1.
2) Перейдем к прямоугольным координатам, используя формулы:
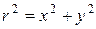 и
и 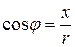 .
.
Подставляя выражение для r и соsj в заданное уравнение
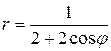 ,
,
получаем:
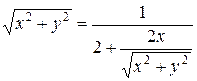 .
.
Выполняем преобразования, чтобы освободиться от знаменателя.
 ;
;
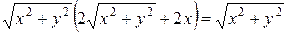 ,
,  ;
;
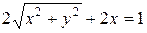 .
.
Перенося 2х в правую часть и возводя в квадрат обе части равенства, имеем:
 .
.
Преобразуя, получаем уравнение кривой в каноническом виде.

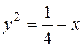 − парабола.
− парабола.
3) Полученное уравнение определяет параболу, ось симметрии которой ось абсцисс, а вершина находится в точке 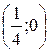 , ветви направлены влево.
, ветви направлены влево.
Данные результаты соответствуют результатам, полученным ранее (см. рис.1.).
Пример 10. Найти характеристические числа и собственные векторы линейного преобразования с матрицей А =  .
.
Решение:
Запишем линейное преобразование в виде: 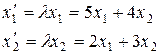
Составим характеристическое уравнение:
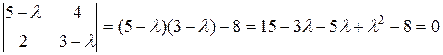
l2 − 8l + 7 = 0;
Корни характеристического уравнения: l1 = 7; l2 = 1;
Для корня l1 = 7: 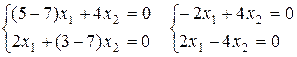
Из системы получается зависимость: x1 – 2x2 = 0. Собственные векторы для первого корня характеристического уравнения имеют координаты: (t; 0,5t) где t − параметр.
Для корня l2 = 1: 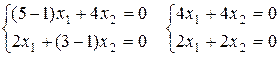
Из системы получается зависимость: x1 + x2 = 0. Собственные векторы для второго корня характеристического уравнения имеют координаты: (t; −t) где t − параметр.
Полученные собственные векторы можно записать в виде:

Пример 11. Дано комплексное число z. Требуется:
1. записать число z в алгебраической и тригонометрической формах;
2. найти все корни уравнения 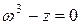 .
.
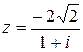 .
.
Решение:
1) Комплексное число z в алгебраической форме имеет вид: z=а+bi;
в тригонометрической форме: z=r(cosj+i×sinj), где 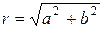 и
и 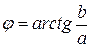 .
.
Для того чтобы записать 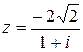 в алгебраической форме, умножим числитель и знаменатель на сопряженное к знаменателю, т. е. на 1− i.
в алгебраической форме, умножим числитель и знаменатель на сопряженное к знаменателю, т. е. на 1− i.
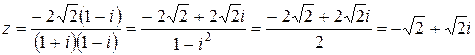 .
.
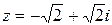 − алгебраическая форма.
− алгебраическая форма.
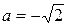 ,
, 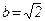 ,
, 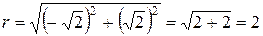 ,
,
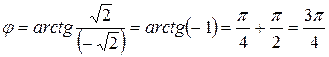 .
.
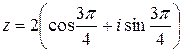 − тригонометрическая форма.
− тригонометрическая форма.
2) 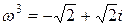 Þ
Þ 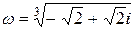 .
.
Так как число 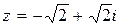 в тригонометрической форме
в тригонометрической форме
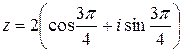 Þ
Þ
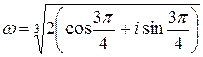 .
.
Применяя формулу для извлечения корня из комплексного числа:
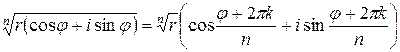 ,
,
получаем 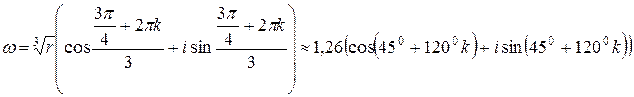
Если k=0, то 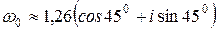 ;
;
Если k=1, то 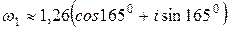 ;
;
Если k=2, то 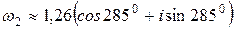 .
.
Следовательно, корни уравнения в алгебраической форме имеет вид
Ответ:
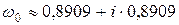 ,
,
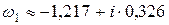 ,
,
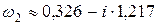 .
.
Пример 12. Даны два линейных преобразования:
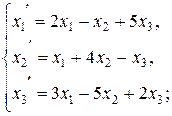
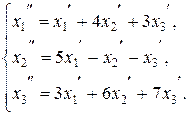
Средствами матричного исчисления найти преобразование, выражающее x1¢¢, x2¢¢, x3¢¢ через x1, x2, x3.
Решение:
Первое преобразование определяется матрицей A, а второе − матрицей B, где
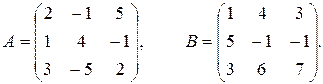
Искомое преобразование является произведением данных преобразований с матрицей
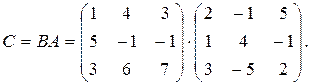
Перемножив матрицы B и A, получим матрицу
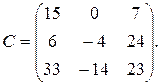
Следовательно, искомое преобразование таково:
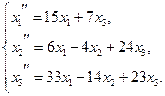
Пример13. В таблице приведены данные об исполнении баланса за отчетный период в усл. ден. ед.:
| Отрасль | Потребление | Конечный продукт | Валовый выпуск | ||
| Энергетика | Машиностроение | ||||
| Производство | Энергетика | ||||
| Машиностроение |
Вычислим необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а в отрасли машиностроения сохранится на прежнем уровне.
Решение.
Математическая модель, позволяющая анализировать связь между отраслями, разработана американским экономистом В. Леонтьевым.
Далее введём обозначения: 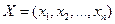 вектор валового объёма продукции;
вектор валового объёма продукции; 
 вектор конечного продукта (для непроизводственного потребления); A − матрица прямых затрат (
вектор конечного продукта (для непроизводственного потребления); A − матрица прямых затрат ( .Коэффициенты
.Коэффициенты 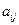 вычисляют по формуле
вычисляют по формуле 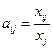
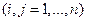 и они показывают затраты продукции
и они показывают затраты продукции 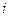 − й отрасли на производство единицы продукции
− й отрасли на производство единицы продукции 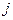 − й отрасли. Здесь
− й отрасли. Здесь 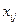 − объём продукции
− объём продукции 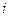 − й отрасли, потребляемой
− й отрасли, потребляемой 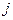 − й отраслью в процессе производства.
− й отраслью в процессе производства.
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска 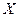 , который при известной матрице
, который при известной матрице  прямых затрат обеспечивает заданный вектор конечного продукта
прямых затрат обеспечивает заданный вектор конечного продукта 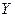 .
.
Математически решение данной задачи в матричном виде можно
представить таким образом: 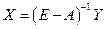 .
.
Имеем
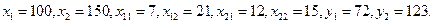
Коэффициенты прямых затрат:
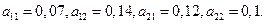
Матрица прямых затрат:
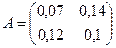
Она является неотрицательной и удовлетворяет критерию продуктивности:
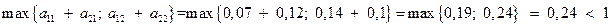 .
.
Поэтому для любого вектора конечного продукта 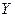 можно найти необходимый объем валового выпуска
можно найти необходимый объем валового выпуска 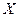 по формуле
по формуле 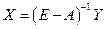 .
.
Определим матрицу полных затрат 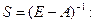
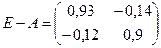
Так как 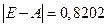 , то
, то
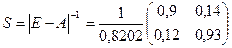
По условию вектор конечного продукта:
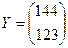
Тогда по формуле 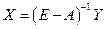 получаем вектор валового выпуска:
получаем вектор валового выпуска:
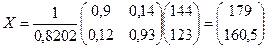 ,
,
т.е. валовой выпуск в энергетической отрасли надо увеличить до 179 усл.ед., а в машиностроительной – до 160,5 усл.ед.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Основы линейной алгебры и аналитической геометрии: Учебно−методическое пособие / В.Г. Шершнев. − М.: НИЦ Инфра−М, 2012. − 168 с.: [Электронный учебник: http://znanium.com]
2. Шевцов, Г.С. Линейная алгебра: теория и прикладные аспекты [Текст]: учеб.пособие / Г.С. Шевцов.— 2−е изд., испр. и доп.— М.: Магистр: ИНФРА−М, 2011.— 528 с.— ГРИФ.
3. Шипачев, В.С. Задачник по высшей математике: учеб.пособие / В.С. Шипачев.— 7−е изд., стер.— М.: Высшая школа, 2007.— 304 с.— ГРИФ.
4. Cборник задач по высшей математике для экономистов: учеб. пособие / под ред. В.И. Ермакова.— М.: ИНФРА−М, 2002, 2003, 2004.— 575 с.
5. Виленкин, И.В. Высшая математика для студентов экономических, технических, естественно−научных специальностей вузов: Учеб.пособие / И.В. Виленкин, В.М. Гробер.— 3−е изд., испр. — Ростов−на−Дону: Феникс, 2005.— 414
6. Власов, В.Г. Конспект лекций по высшей математике [Текст] / В.Г. Власов.— М.: АЙРИС, 1996.— 288 с.
7. Выгодский, М.Я. Справочник по высшей математике / М.Я. Выгодский.— Изд.14−е.— М.: Джангар, Большая медведица, 2001.— 864с.
8. Высшая математика: Учебное пособие / Ю.М.Данилов,Л.Н.Журбенко,Г.А.Никонова,В.В.Кондратьев.— Казань: КХТИ, 1993.— 94с.
9. Высшая математика [Текст]: методические указания и контрольные задания.— Казань, 1993.— 36 с.
10. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1 / П.Е. Данко [и др.].— 6−е изд. — М.: "Оникс": "Мир и Образование", 2007.— 304с.
11. Высшая математика для экономистов: учеб.пособие / под ред. Н.Ш. Кремера.— М.: Банки и биржи: ЮНИТИ, 1997.— 439 с.— ГРИФ.
12. Колесников, А.Н. Краткий курс математики для экономистов: Учебное пособие / А.Н. Колесников.— М.: ИНФРА−М, 1997,2003.— 208с.
13. Контрольные задания по высшей математике на 2−й семестр: Для студентов первого курса экономического факультета.— Нижнекамск, 1998.— 6с.
14. Костромин, А.В. Методические указания по выполнению контрольной работы по математике: для студентов заочного отделения экономического факультета / А.В. Костромин.— Казань: "Таглимат" ИЭУиП, 2000.— 33 с.
15. Красс, М.С. Математика для экономических специальностей: учебник / М.С. Красс.— М.: ИНФРА−М, 1998.— 464с.
16. Кремер, Н.Ш. Практикум по высшей математике для экономистов: Учеб.пособие: Гриф МО РФ / Н.Ш. Кремер, И.М. Тришин, Б.А. Путко и др.; Под ред. Н.Ш. Кремера.— М.: ЮНИТИ−ДАНА, 2005.— 423с.
17. Математика в примерах и задачах: учеб. пособие; Гриф МО РФ / Л. Н. Журбенко и [и др.].— М.: ИНФРА−М, 2009.— 373с.
18. Математика для экономического бакалавриата: Учебник / М.С. Красс, Б.П. Чупрынов. − М.: ИНФРА−М, 2011. − 472 с. [Электронный учебник: http://znanium.com/bookread.php?book=221082]
19. Общий курс высшей математики для экономистов: Учебник; Под ред. В.И. Ермакова. − М.: ИНФРА−М, 2010. − 656 с. [Электронный учебник: http://znanium.com/]
20. Справочник по математике для экономистов/Под ред.В.И.Ермакова.— Изд.2−е, переработ. и доп., илл. — М.: Высшая школа, 1997.— 384с.
21. Шершнев В. Г. Линейная алгебра. Часть I. Основы линейной алгебры: Учебно−методическое пособие для студентов I курса. − М.: Издательство «Менеджер», 2007. – 128 с.: [Электронный учебник: http://znanium.com/bookread.php?book=347840]
1. Шипачев, В.С. Высшая математика: Учебник для вузов: Гриф / В.С. Шипачев.— 9−е изд., стер. — М.: Высшая школа, 2008.— 479с.
Date: 2015-04-23; view: 648; Нарушение авторских прав