
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Перечень экзаменационных вопросов
|
|
1. Матрицы и ее виды: диагональная, единичная, треугольная, симметрическая.
2. Основные операции над матрицами и их свойства (сложение, вычитание).
3. Основные операции над матрицами (умножение на число, умножение матриц).
4. Основные операции над матрицами (степень матрицы, транспонирование).
5. Понятие определителя. Определитель второго и третьего порядков. Правило треугольников, Саррюса.
6. Основные свойства определителей.
7. Определитель 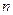 −ого порядка. Миноры и алгебраические дополнения.
−ого порядка. Миноры и алгебраические дополнения.
8. Теорема Лапласа (формулировка), вычисление определителя методом разложения по элементам 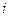 −ой строки или
−ой строки или 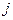 −ого столбца.
−ого столбца.
9. Понятие обратной матрицы. Условие существования обратной матрицы.
10. Нахождение обратной матрицы методом элементарных преобразований.
11. Понятие ранга матрицы, эквивалентные матрицы, различные способы нахождения ранга матрицы.
12. Понятие системы линейных уравнений и ее решения. Теорема Кронекера−Капелли.
13. Решение системы линейных неоднородных уравнений методом Гаусса.
14. Формулы Крамера для решения системы линейных неоднородных уравнений.
15. Матричный способ решения линейных уравнений.
16. Однородные системы линейных уравнений, Фундаментальная система решений.
17. Понятие вектора. Линейные операции над векторами: умножение, вычитание, сложение.
18. Базис, размерность векторного пространства: запись вектора через единичные вектора.
19. Декартова прямоугольная система координат.
20. Скалярное произведение двух векторов его свойства (определение, свойства, геометрический смысл, смешанное произведение векторов, заданных своими координатами).
21. Скалярное произведение векторов, заданными своими координатами. Длина вектора. Направляющие косинусы вектора. Единичный вектор.
22. Векторное произведение двух векторов (определение, свойства, геометрический смысл, векторное произведение векторов, заданных своими координатами).
23. Смешанное произведение трех векторов (определение, свойства, геометрический смысл, смешанное произведение векторов, заданных своими координатами).
24. Направляющий вектор прямой. Уравнений прямой в векторной форме.
25. Общее уравнение прямой. Частные случаи.
26. Различные виды прямой на плоскости (с угловым коэффициентом в отрезках уравнение прямой проходящей через две заданные точки).
27. Уравнение прямой, проходящей через заданную точку, с заданным угловым коэффициентом.
28. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых на плоскости.
29. Эллипс, его каноническое уравнение. Характеристики эллипса.
30. Гипербола, ее каноническое уравнение. Характеристики гиперболы.
31. Парабола, ее каноническое уравнение. Характеристики параболы.
32. Комплексные числа (алгебраическая форма). Действия с комплексными числами.
33. Комплексные числа (тригонометрическая форма). Действия с комплексными числами.
Date: 2015-04-23; view: 541; Нарушение авторских прав