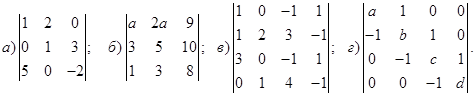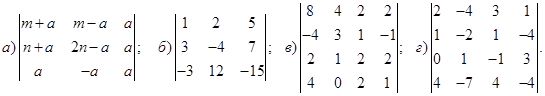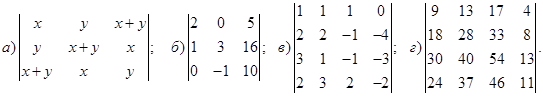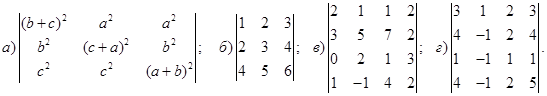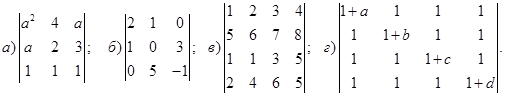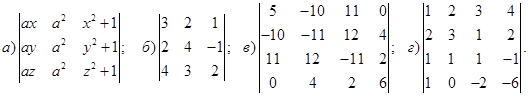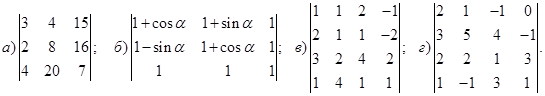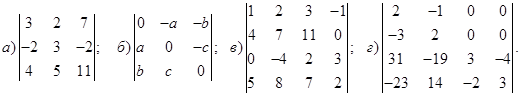Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания к контрольной работе
|
|
1−10. Вычислить определители и найти для них 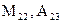
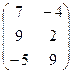
11−20. Даны матрицы  и
и 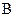 . Вычислить
. Вычислить 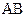 и
и 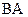 , если они существуют.
, если они существуют.
| Вариант | Матрица 
| Матрица 
|
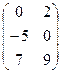
| 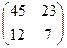
| |
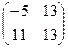
| 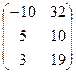
| |

| 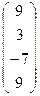
| |
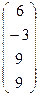
| 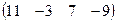
| |
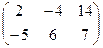
| 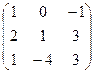
| |
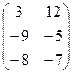
| 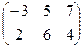
| |
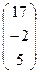
| 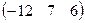
| |
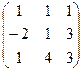
| 
| |
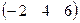
| 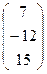
| |
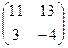
| 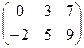
|
21−30. Найти матрицу, обратную данной. Выполнить проверку.
| Вариант | Матрица 
| Вариант | Матрица 
|
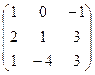
| 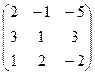
| ||
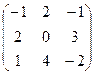
| 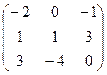
| ||
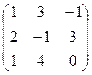
| 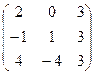
| ||
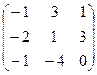
| 
| ||
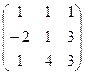
| 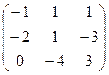
|
31−40. Доказать совместность данной системы линейных уравнений и решить ее тремя способами: 1) методом Крамера; 2) методом Гаусса; 3) средствами матричного исчисления.
31. 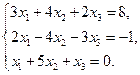 32.
32. 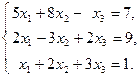
33. 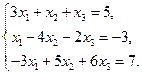 34.
34. 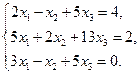
35. 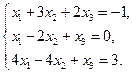 36.
36. 
37. 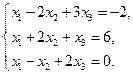 38.
38. 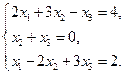
39. 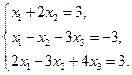 40.
40. 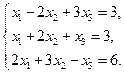
41−50. Решить систему методом Гаусса. Найти общее и два частных решения системы.
41. 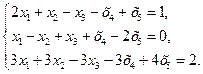 42.
42. 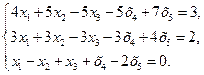
43. 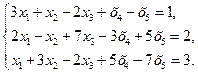 44.
44. 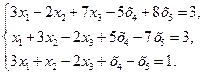
45. 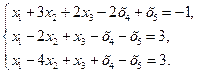 46.
46. 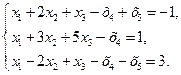
47. 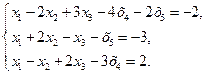 48.
48. 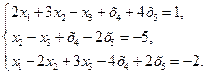
49. 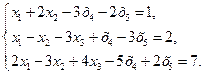 50.
50. 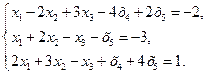
51−60. Убедиться, что векторы 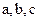 образуют базис. Найти разложение вектора
образуют базис. Найти разложение вектора 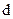 по этому базису.
по этому базису.
| Номер задачи | Координаты векторов | |||
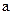
| 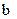
| 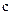
| 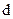
| |
| 51. | 3; 2; 2 | 2; 3; 1 | 1; 1; 3 | 5; 1; 1 |
| 52. | 1; 2; 1 | −1; 1; 2 | 1; 1; 2 | 6; 3; 5 |
| 53. | 1; −2; 1 | −2; 0; 4 | 1; 3; 3 | 5; −1; 1 |
| 54. | 1; 2; 4 | 1; −1; 1 | 2; 2; 4 | −1; −4; −2 |
| 55. | 2; 3; 3 | −1; 4; −2 | −1; −2; 4 | 4; 11; 11 |
| 56. | 3; 2; 2 | 2; 3; 1 | 1; 1; 3 | 5; 1; 11 |
| 57. | 3; 2; −2 | 4; −1; 3 | 1; 0; 1 | 4; 7; 11 |
| 58. | 5; −1; 4 | 1; 2; 3 | 4; −2; 1 | 0; 4; 2 |
| 59. | 1; 1; 3 | 2; 3; 1 | 3; 2; 2 | 5; 1; 1 |
| 60. | 2; 1; 1 | 2; −4; 3 | −1; 2; 1 | 6; 0; 5 |
61−70. Даны координаты вершин пирамиды 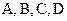 . Требуется найти: 1) длину ребра
. Требуется найти: 1) длину ребра 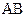 ; 2) угол между ребрами
; 2) угол между ребрами 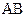 и
и 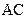 ; 3) уравнение прямой
; 3) уравнение прямой 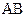 ; 4) уравнение плоскости
; 4) уравнение плоскости 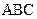 ; 5) угол между ребром
; 5) угол между ребром 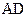 и гранью
и гранью 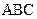 ; 6) площадь грани
; 6) площадь грани 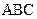 ; 7) объем пирамиды; 8) уравнение высоты, опущенной из вершины
; 7) объем пирамиды; 8) уравнение высоты, опущенной из вершины 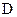 на грань
на грань 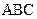 . Сделать чертеж.
. Сделать чертеж.
61. 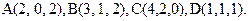
62. 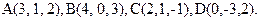
63. 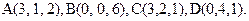
64. 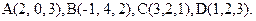
65. 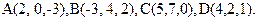
66. 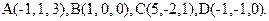
67. 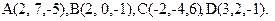
68. 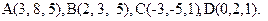
69. 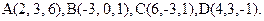
70. 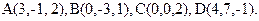
71−80. Даны вершины треугольника 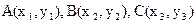 . Требуется: 1) вычислить длину высоты и медианы, проведенных из вершин
. Требуется: 1) вычислить длину высоты и медианы, проведенных из вершин 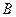 ; написать их уравнения; 2) написать уравнение прямой, проходящей через вершину
; написать их уравнения; 2) написать уравнение прямой, проходящей через вершину 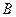 параллельно стороне
параллельно стороне 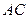 ; 3) угол между прямыми
; 3) угол между прямыми 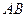 и
и 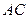 ; 4) найти точку
; 4) найти точку 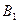 симметричную точке
симметричную точке 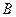 относительно прямой
относительно прямой 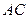 .
.
| Номер задачи | Координаты вершин треугольника | ||

| 
| 
| |
| 71. | 4; 3 | −2:−3 | −5; 5 |
| 72. | 4;−2 | −4; 4 | −3; 1 |
| 73. | 2; 6 | −4; 3 | −5;−2 |
| 74. | −1;−1 | −2; 6 | 4; 3 |
| 75. | −2; 6 | 1;−1 | 6; 3 |
| 76. | 7; 2 | −1; 4 | −2; −3 |
| 77. | 3; 1 | −1; 4 | 2;−2 |
| 78. | 7; 1 | −5;−4 | 4;−3 |
| 79. | 6; 2 | 3;−5 | −2; 7 |
| 80. | −2;−3 | −4; 5 | 1;−3 |
81−90. Линия задана уравнением 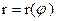 в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
1. построить линию по точкам, начиная от 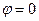 до
до 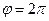 и придавая
и придавая 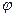 значения через промежуток
значения через промежуток 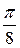 ;
;
2. найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью;
3. по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
81. 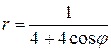 ; 82.
; 82. 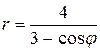 ;
;
83. 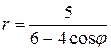 ; 84.
; 84. 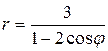 ;
;
85. 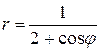 ; 86.
; 86. 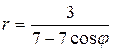 ;
;
87. 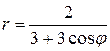 ; 88.
; 88. 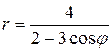 ;
;
89. 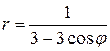 ; 90.
; 90. 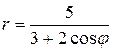 .
.
91−101. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей  .
.
91. 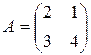 . 92.
. 92. 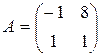 .
.
93. 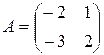 . 94.
. 94. 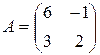 .
.
95. 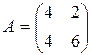 . 96.
. 96. 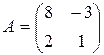 .
.
97. 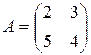 . 98.
. 98. 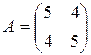 .
.
99. 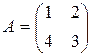 . 100.
. 100. 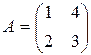 .
.
101−110. Дано комплексное число 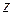 . Требуется: 1) записать его в алгебраической и тригонометрической формах; 2) найти все корни уравнения
. Требуется: 1) записать его в алгебраической и тригонометрической формах; 2) найти все корни уравнения 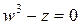 .
.
101. 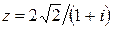 . 102.
. 102. 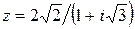 .
.
103. 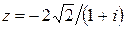 . 104.
. 104. 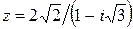 .
.
105. 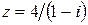 . 106.
. 106. 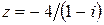 .
.
107. 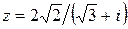 . 108.
. 108. 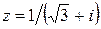 .
.
109. 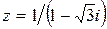 . 110.
. 110. 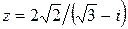 .
.
111−120. Даны два линейных преобразования:
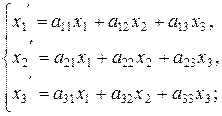
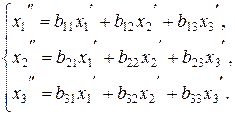
Средствами матричного исчисления найти преобразование, выражающее 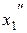 ,
, 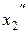 ,
, 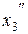 через
через 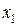 ,
, 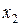 ,
, 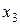 .
.
111. 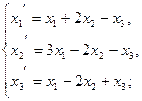
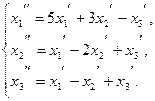
112. 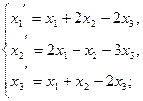
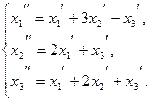
113. 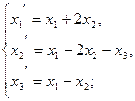
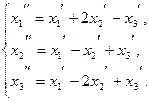
114. 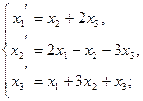
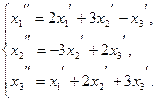
115. 
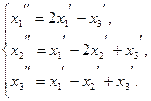
116. 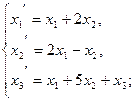
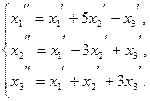
117. 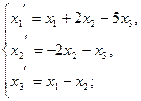
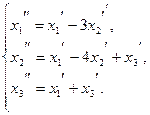
118. 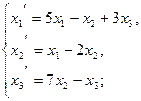
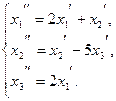
119. 
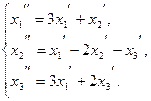
120. 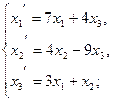
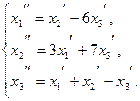
121−130. В таблице приведены данные об исполнении баланса за отчетный период в усл. ден. ед. Вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт первой отрасли должен увеличится в 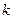 раз, а второй отрасли − на
раз, а второй отрасли − на 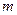 %.
%.
121. 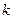 = 1.5,
= 1.5, 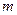 = 30%.
= 30%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
122. 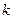 = 1,
= 1, 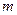 = 20%.
= 20%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
123. 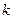 = 2,
= 2, 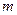 = 50%.
= 50%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
124. 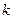 = 2.5,
= 2.5, 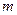 = 0%.
= 0%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
125. 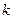 = 1.5,
= 1.5, 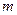 = 150%.
= 150%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
126. 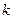 = 1.2,
= 1.2, 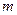 = 30%.
= 30%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
127. 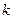 = 1.4,
= 1.4, 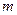 = 70%.
= 70%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
128. 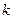 = 2.5,
= 2.5, 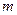 = 80%.
= 80%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
129. 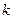 = 2,
= 2, 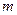 = 90%.
= 90%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
130. 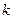 = 1,
= 1, 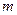 = 50%.
= 50%.
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | |||||
РЕШЕНИЕ ТИПОВОГО ВАРИАНТА
Пример 1. Вычислить определители и найти для них 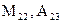 :
:
а) 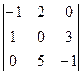 ; б)
; б) 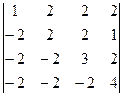 .
.
Решение:
Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения: 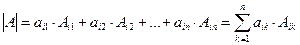 . Алгебраическим дополнением
. Алгебраическим дополнением 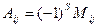 некоторого элемента определителя называется минор этого элемента, умноженный на (−1)S, где
некоторого элемента определителя называется минор этого элемента, умноженный на (−1)S, где 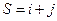 – сумма номеров строки и столбца, на пересечении которых стоит данный элемент. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
– сумма номеров строки и столбца, на пересечении которых стоит данный элемент. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Выберем в рассматриваемом определителе любую строку. Например, первую строку. Тогда определитель может быть вычислен по формуле
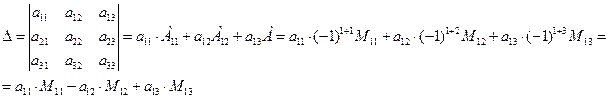

 где
где 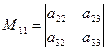 − минор элемента
− минор элемента 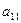 , полученный вычеркиванием из исходного определителя первой строки и первого столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и первого столбца, на пересечении которых находится элемент 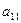 :
: 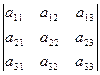 ,
,


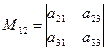 − минор элемента
− минор элемента 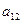 , полученный вычеркиванием из исходного определителя первой строки и второго столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и второго столбца, на пересечении которых находится элемент 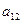 :
: 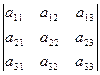 ,
,


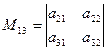 − минор элемента
− минор элемента 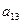 , полученный вычеркиванием из исходного определителя первой строки и третьего столбца, на пересечении которых находится элемент
, полученный вычеркиванием из исходного определителя первой строки и третьего столбца, на пересечении которых находится элемент 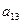 :
: 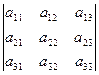 .
.
Выполним задание для первого определителя:
М22 = 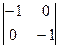 = (−1) × (−1) – 0 × 0 = 1 – 0 = 1,
= (−1) × (−1) – 0 × 0 = 1 – 0 = 1,
А23 = (−1)2+3 × М23 = (−1) × ((−1)×5 − 2×0) = 5.
Вычислим определитель, разложив его по элементам первой строки: 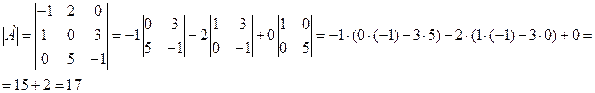 .
.
б) Выполним задание для второго определителя, раскрывая все определители по элементам первой строки:
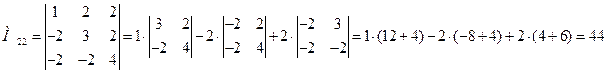
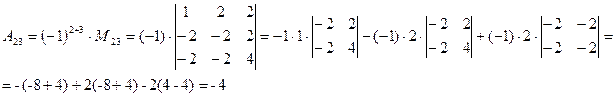
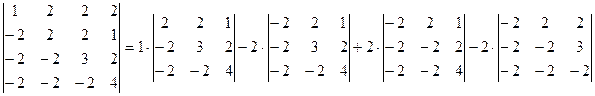 .
.
Полученные определители третьего порядка сведем к определителям второго порядка, еще раз разложив каждый из них по первой строке.
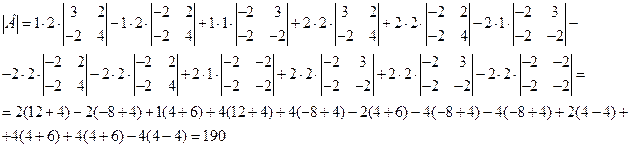 Ответ: а)
Ответ: а) 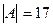 ,
, 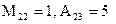 ; б)
; б) 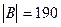 ,
, 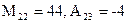 .
.
Пример 2. Даны матрицы  и
и 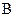 . Вычислить
. Вычислить 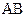 и
и 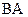 , если они существуют:
, если они существуют:
а) 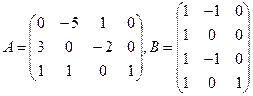 ;
;
Решение:
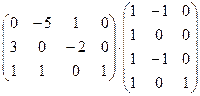
определим размер матрицы, которую получим в результате умножения: первая матрица имеет размер 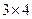 , вторая −
, вторая − 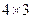 . Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер
. Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер 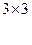 .
.
Для того, чтобы найти элемент 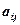 необходимо
необходимо 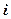 − ю строку первой матрицы умножить скалярно на
− ю строку первой матрицы умножить скалярно на 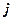 −й столбец второй матрицы
−й столбец второй матрицы
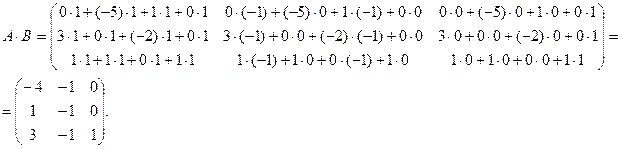
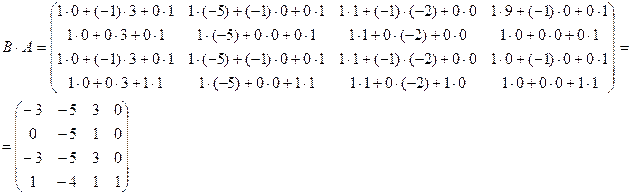 Ответ:
Ответ: 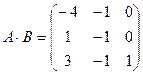 ;
; 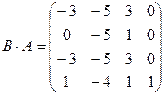 .
.
Пример 3. Определить, имеет ли данная матрица обратную, найти обратную матрицу к данной 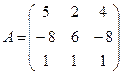 .
.
Решение:
Обратную матрицу к данной матрице  будем находить по следующему плану:
будем находить по следующему плану:
1. Вычислим определитель матрицы 
2. Вычислим алгебраические дополнения для всех элементов матрицы  по формуле
по формуле
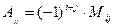 ,где
,где 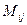 минор элемента
минор элемента 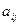 матрицы
матрицы 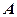 .
.
3. Запишем матрицу 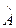 , элементами которой являются соответствующие алгебраические дополнения
, элементами которой являются соответствующие алгебраические дополнения
4. Найдем транспонированную матрицу 
5. Найдем обратную матрицу по формуле 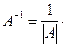

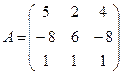
1. Вычислим определитель матрицы 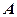 по формуле
по формуле
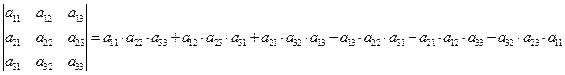
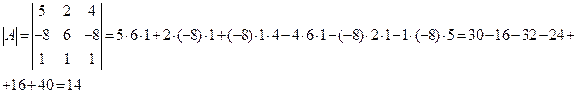
2. Вычислим алгебраические дополнения для всех элементов матрицы 
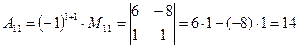
(для вычисления минора 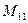 вычеркиваем в матрице
вычеркиваем в матрице  первую строку и первый столбец)
первую строку и первый столбец)
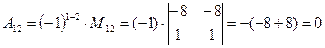
(для вычисления минора 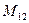 вычеркиваем в матрице
вычеркиваем в матрице  первую строку и второй столбец)
первую строку и второй столбец)
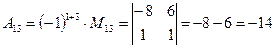
(для вычисления минора 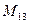 вычеркиваем в матрице
вычеркиваем в матрице  первую строку и третий столбец)
первую строку и третий столбец)
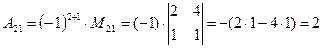
(для вычисления минора 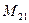 вычеркиваем в матрице
вычеркиваем в матрице  вторую строку и первый столбец)
вторую строку и первый столбец)
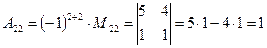
(для вычисления минора 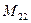 вычеркиваем в матрице
вычеркиваем в матрице  вторую строку и второй столбец)
вторую строку и второй столбец)
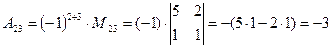
(для вычисления минора 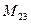 вычеркиваем в матрице
вычеркиваем в матрице  вторую строку и третий столбец)
вторую строку и третий столбец)
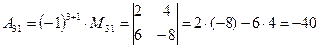
(для вычисления минора 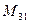 вычеркиваем в матрице
вычеркиваем в матрице  третью строку и первый столбец)
третью строку и первый столбец)
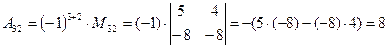
(для вычисления минора 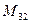 вычеркиваем в матрице
вычеркиваем в матрице  третью строку и второй столбец)
третью строку и второй столбец)
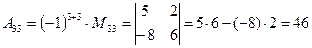
(для вычисления минора 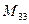 вычеркиваем в матрице
вычеркиваем в матрице  третью строку и третий столбец)
третью строку и третий столбец)
3. Запишем матрицу 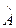 , элементами которой являются найденные алгебраические дополнения
, элементами которой являются найденные алгебраические дополнения
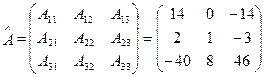
4. Найдем транспонированную матрицу  (строки становятся столбцами, а столбцы – строками с сохранением порядка)
(строки становятся столбцами, а столбцы – строками с сохранением порядка)

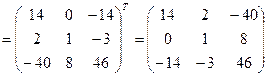
5. Найдем обратную матрицу
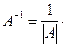

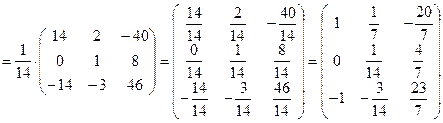
Произведем проверку. Для этого найдем произведения 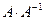 и
и 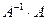 . Если окажется, что они равны
. Если окажется, что они равны 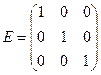 , то матрица
, то матрица 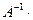 найдена верно.
найдена верно.
Имеем
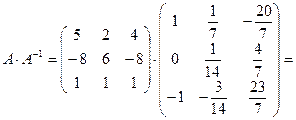
определим размер матрицы, которую получим в результате умножения: первая матрица имеет размер 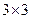 , вторая −
, вторая − 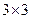 . Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер
. Берем количество строк у первой матрицы, а количество столбцов – у второй. Таким образом, получаем размер 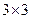 .
.
Для того, чтобы найти элемент 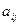 необходимо
необходимо 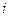 − ю строку первой матрицы умножить скалярно на
− ю строку первой матрицы умножить скалярно на 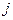 −й столбец второй матрицы
−й столбец второй матрицы
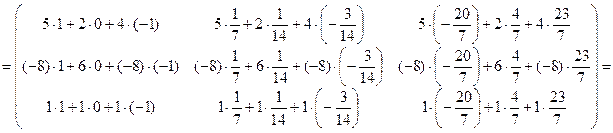
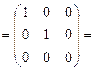
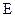 .
.
аналогично находим произведение 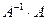 :
:
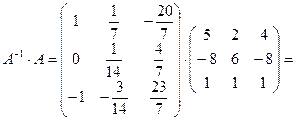
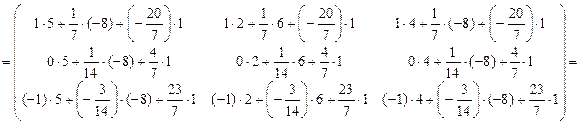

Ответ: 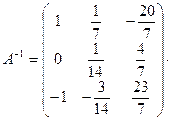
Пример 4. Дана система линейных уравнений:
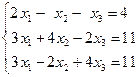
доказать ее совместность и решить тремя способами:
1) Методом Гаусса;
2) По формулам Крамера;
3) Средствами матричного исчисления.
Решение:
Теорема Кронекера−Капелли. Система совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу ее расширенной матрицы, т. е. 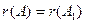 , где
, где
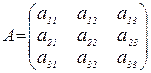 ,
, 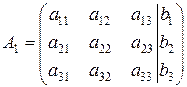 .
.
Расширенная матрица системы имеет вид:
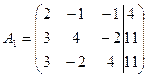 .
.
Умножим первую строку на (–3),а вторую на (2); прибавим после этого элементы первой строки к соответствующим элементам второй строки; вычтем из второй строки третью. В полученной матрице первую строку оставляем без изменений.
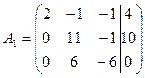 ~
~
Разделим элементы третьей строки на (6) и поменяем местами вторую и третью строки:
~ 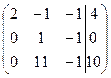 ~
~
Умножим вторую строку на (–11) и прибавим к соответствующим элементам третьей строки.
~ 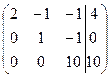
Разделим элементы третьей строки на (10).
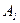 ~
~ 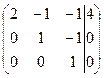 ;
; 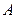 ~
~ 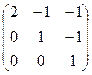 .
.
Найдем определитель матрицы А.
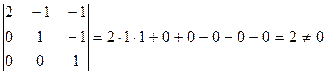 .
.
Следовательно, 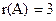 . Ранг расширенной матрицы
. Ранг расширенной матрицы 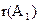 так же равен 3, т.е.
так же равен 3, т.е.
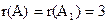 Þ система совместна.
Þ система совместна.
1) Исследуя систему на совместность, расширенную матрицу преобразовали по методу Гаусса.
Метод Гаусса состоит в следующем:
1. Приведение матрицы к треугольному виду, т. е. ниже главной диагонали должны находиться нули (прямой ход).
2. Из последнего уравнения находим 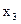 и подставляем его во второе, находим
и подставляем его во второе, находим 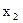 , и зная
, и зная 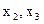 подставляем их в первое уравнение, находим
подставляем их в первое уравнение, находим 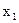 (обратный ход).
(обратный ход).
Запишем, преобразованную по методу Гаусса, расширенную матрицу
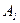 ~
~ 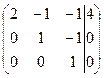
в виде системы трех уравнений:
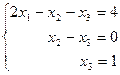 Þ
Þ 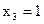
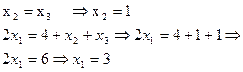
Ответ: 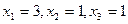 .
.
2) Решим систему по формулам Крамера: если определитель системы уравнений Δ отличен от нуля, то система имеет единственное решение, которое находится по формулам
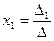 ;
; 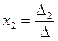 ;
; 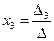 .
.
Вычислим определитель системы Δ:
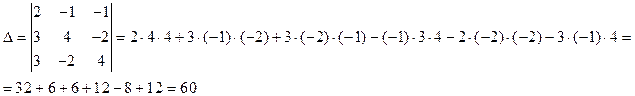 Т.к. определитель системы отличен от нуля, то согласно правилу Крамера, система имеет единственное решение. Вычислим определители
Т.к. определитель системы отличен от нуля, то согласно правилу Крамера, система имеет единственное решение. Вычислим определители 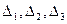 . Они получаются из определителя системы
. Они получаются из определителя системы  заменой соответствующего столбца на столбец свободных коэффициентов.
заменой соответствующего столбца на столбец свободных коэффициентов.
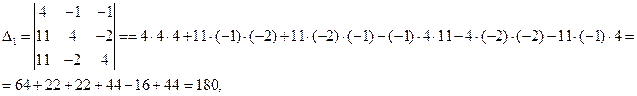
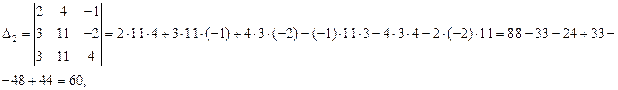
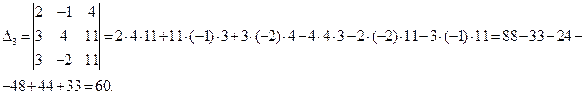
Находим по формулам неизвестные:
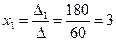 ;
; 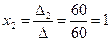 ;
; 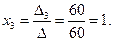
Ответ: 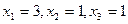 .
.
3) Решим систему средствами матричного исчисления, т. е. при помощи обратной матрицы.
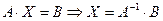 , где
, где 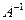 – обратная матрица к
– обратная матрица к 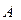 ,
,
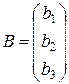 − столбец свободных членов,
− столбец свободных членов,
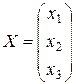 − матрица−столбец неизвестных.
− матрица−столбец неизвестных.
Обратная матрица считается по формуле:
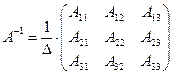 (*)
(*)
где  − определитель матрицы
− определитель матрицы  ,
, 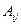 – алгебраические дополнения элемента
– алгебраические дополнения элемента 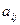 матрицы
матрицы  .
. 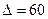 (из предыдущего пункта). Определитель отличен от нуля, следовательно, матрица А обратима, и обратную к ней матрицу можно найти по формуле (*). Найдем алгебраические дополнения для всех элементов матрицы
(из предыдущего пункта). Определитель отличен от нуля, следовательно, матрица А обратима, и обратную к ней матрицу можно найти по формуле (*). Найдем алгебраические дополнения для всех элементов матрицы  по формуле:
по формуле: 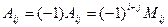
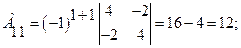
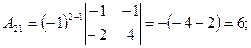
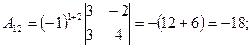
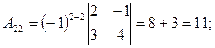
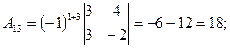
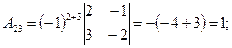
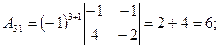
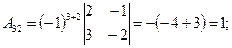
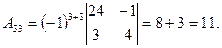
Запишем обратную матрицу.
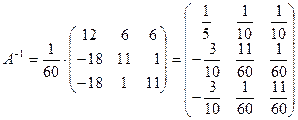 .
.
Сделаем проверку по формуле: 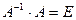
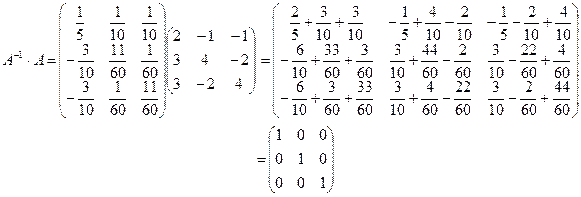
Вывод: так как произведение 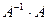 дает единичную матрицу, то обратная матрица
дает единичную матрицу, то обратная матрица 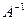 найдена верно и решение системы определяется по формуле
найдена верно и решение системы определяется по формуле 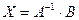
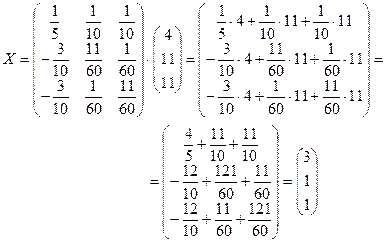 .
.
Ответ: 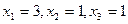 .
.
Проверка. Подставим полученные значения в систему. Получим:
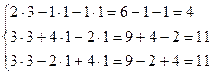
Т. к. неизвестные  обратили каждое уравнение в тождество, то они найдены верно.
обратили каждое уравнение в тождество, то они найдены верно.
Пример 5. Решить систему методом Гаусса и найти какие-нибудь два базисных решения системы.
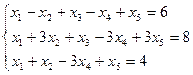
Решение:
Date: 2015-04-23; view: 665; Нарушение авторских прав