Понятие о квантовой статистике Бозе — Эйнштейна и Ферми — Дирака

Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ. Это связано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невза­имодействующих частиц задается с помощью так называемых чисел заполнения Ni — чисел, указывающих степень заполнения квантового состояния (характеризуется данным набором i квантовых чисел) частицами системы, состоящей из многих тождест­венных частиц.

Для систем частиц, образованных бозонами — частицами с нулевым или целым спином, числа заполнения могут принимать любые целые значения: 0, 1, 2,...

Для систем частиц, образованных фермионами — частицами с полуцелым спином, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых.

Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна

Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым

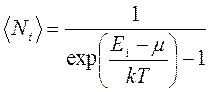
Это распределение называется распределением Бозе — Эйнштейна. Здесь <N> — сред­нее число бозонов в квантовом состоянии с энергией E_i

Т— термодинамическая температура,

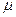— химический потенциал;

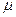не зависит от энергии, а определяется только температурой и плотностью числа частиц.

Химический потенциал находится обычно из условия, что сумма всех <N> равна полному числу частиц в системе. Здесь так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фик­сированы.

Статистика Ферми-Дирака

Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми — Дирака. Распределение фермионов по энергиям имеет вид

Распределение Ферми-Дирака для вырожденного электронного газа в металлах

Электроны проводимости а металле можно рассматривать как идеальный газ в потенциальном ящике с плоским дном.

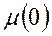- химический потенциал

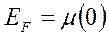- энергия Ферми, максимальная энергия, которую могут иметь электроны при Т=0К.

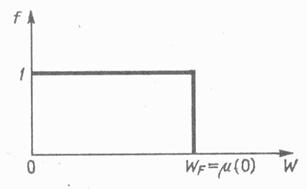
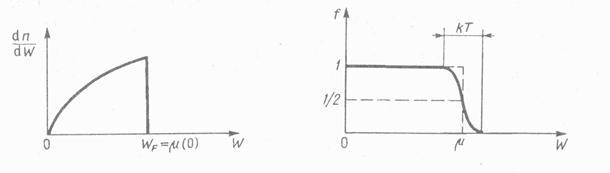
Распределение электронов по энергиям

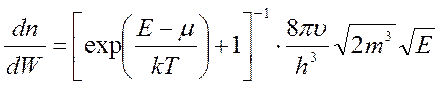
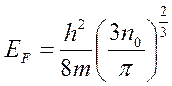
где 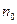- концентрация электронов проводимости

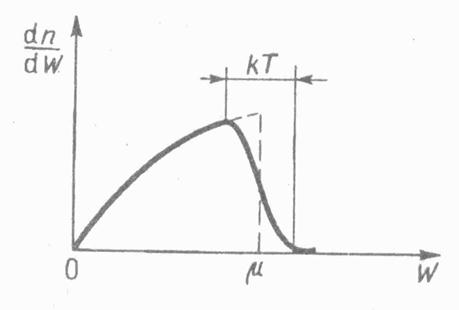
Электронный газ в металлах всегда сильно вырожден. Температура вырождения газа составляет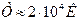

Средняя энергия электрона проводимости в металлах

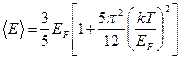
Date: 2015-05-18; view: 988; Нарушение авторских прав