
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вывод выражения для излучательной способности
|
|
Это выражение впервые было получено М.Планком, который, опираясь на известный ему экспериментальный материал, предположил, что энергия световой волны пропорциональна не квадрату ее амплитуды, а частоте n, т.e. Есв = hn, где h - коэффициент пропорциональности, известный теперь как постоянная Планка (h = 6,62× 10 -34 Дж сек.), причем про-цесс излучения происходит не непрерывно, а отдельными порциями - квантами. В связи с этим предположением энергия диполей также изменяется скачком от E1 до Е2. Однако мы приведем более простой вывод, принадлежащий А.Эйнштейну. Основная идея этого вывода состоит в том, что кроме спонтанных актов излучения, происходящих с вероятностью А i k существуют вынуженные элементарные акты излучения и поглощения под действием внеш-ней периодической силы, вероятности которых Вi k или Вk i, в зависимости от направления перехода.
Рассмотрим систему, состоящую из большого числа (No) диполей, находящуюся в сос-тоянии равновесия с тепловым излучением, спектральная плотность энергии которого(т.е. излучательная способность) равна en,Т.
Обозначим энергию диполя до момента излучения через E1, a энергию диполей после излучения – E2; число диполей в состояниях е1 и Е2 - через N1и N2. Количество спонтанных переходов из состояния с энергией е1 в состояние с энергией Е2 равно D 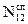 = A 12 N1.B то же время под действием теплового излучения, характеризующегося излучательной способ-ностью en,Т происходят вынужденные переходы как из состояния 1 в состояние 2, так и обратно.Число этих переходов равно D
= A 12 N1.B то же время под действием теплового излучения, характеризующегося излучательной способ-ностью en,Т происходят вынужденные переходы как из состояния 1 в состояние 2, так и обратно.Число этих переходов равно D 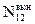 = n1В12 en,Т, D
= n1В12 en,Т, D 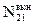 = N2 B21en,Т.
= N2 B21en,Т.
В состоянии теплового равновесия число переходов из состояния I в состояние 2 должно равняться числу переходов из состояния 2 в состояние l.Ha основании этого запишем D 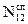 + D
+ D 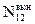 = D
= D 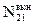 или А12N1 +n1В12 en,Т = N2 B21en,Т.
или А12N1 +n1В12 en,Т = N2 B21en,Т.
Отсюда находим en,Т:
en,Т = 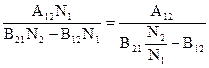 .
.
Для оценки отношения N2 / n1 используем представления классической статистики, позволяющей на основании распределения Больцмана вычислить число частиц с заданной энергией:
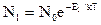 ;
; 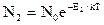 , где N0 -общее число частиц в системе. Отсюда
, где N0 -общее число частиц в системе. Отсюда
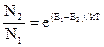 .
.
Тогда с учетом того, что, как показывает эксперимент,В12 =В 21, получим
en,Т = 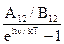 .
.
В последнем выражении использовано представление Планка, что E1 –E2 = hn. Отношение A12 / B12 не может быть вычислено в нашем курсе. Строгий расчет показывает, что оно рав-но hn3 /с2, где с – скорость света. Поэтому выражение для излучательной способности при-обретает следующий вид:
en,Т = 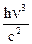
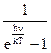 .
.
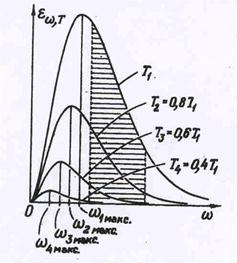 Рис. Зависимость излучатель-
ной спосбности от частоты и
температуры.
Рис. Зависимость излучатель-
ной спосбности от частоты и
температуры.
| Графическая зависимость излучательной способности приведена на рис.61, где по оси частот отложена угло-вая частота w = 2nn.
Законы Стефана- Больцмана и Вина.
Из рис. видно, что для каждой температуры излучательная способность имеет максимальное значение при определенной частоте излучения. Для определения этой частоты проведем исследова-ние на экстремум величины en,Т , предварительно проведя замену перемен-ной в целях сокращения записи. Введем новую переменную х:
х = 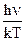 ;
тогда n = ;
тогда n = 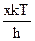 ; n3 = ; n3 = 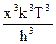 и dn = и dn = 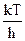 dx.
Теперь выражение для излучательной способности приобретает такой вид: dx.
Теперь выражение для излучательной способности приобретает такой вид:
|
en,Т = 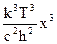
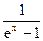 .
.
Вычисляя первую производную и сокращая полученный результат на постоянную величи-ну, имеем:
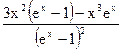 = 0.
= 0.
Из этого выражения видно, что оно равно нулю, если числитель дроби равен нулю, откуда для определения экстремального значения х получаем трансцендентное уравнение:
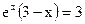 .
.
Можно показать,что это уравнение имеет решение (приближенное значение х м =2,8214), для простоты обозначим его а',т.е. х М = а', или hnМ / kT = а', откуда следует закон Вина:
nМ =аТ.
В этом выражении постоянная а является комбинацией других постоянных: а = a’, k / h.
Определим интегральную излучательную способность Ет (она называется энергети-ческой светимостью) как еT = 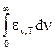 , или в обозначениях новой переменной:
, или в обозначениях новой переменной:
ET = 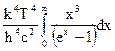 .
.
Интеграл в этом выражении является табличным,его величина равна л4 / 15.0бозначая через s комбинацию постоянных 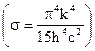 получаем следующее выражение для энергети-ческой светимости: ЕТ = sТ4, которое известно как закон Стефана-Больцмана.
получаем следующее выражение для энергети-ческой светимости: ЕТ = sТ4, которое известно как закон Стефана-Больцмана.
Сравним теоретические выводы с практикой.Экспериментальные данные показывают,.что при комнатной температуре максимум излучения лежит в далекой инфракрасной об-ласти, излучение в видимой области практически отсутствует. При температуре, приближающейся к 1000 К, максимум по-прежнему в инфракрасной области, однако и из-лучение в видимой части спектра становится заметным (см.рис.61). В силу того, что интен-сивность от длинных, красных волн, к коротким, фио-летовым, падает, наибольшая интен-сивность излучения приходится на красную часть спектра - это температура «красного каления». По мере роста температуры различие в интенсивностях падает, излучение приоб-ретает желтый, а затем белый цвет. При температуре между 5000 и 6000° К максимум про-ходит через область спектра, к которой человеческий глаз наиболее чувствителен. Тем-пературе 5900 К отвечает температура поверхности Солнца, лучеиспускательная способ-ность которого близка к лучеиспускательной способности абсолютно черного тела. Такое излучение воспринимается глазом как белый, дневной свет. При более высоких температурах максимум смещается в ультрафиолетовую область, а интенсивность в фиолетово - голубой области становится большей, чем в красной. Излучение приобретает голубой оттенок.
В 1884 г. Генрих Герц (1857-1894), бывший ученик и ассистент Гельмгольца, приступил к изучению теории Максвелла. В 1887 г. он повторил опыты Гельмгольца с двумя индукционными катушками. После нескольких попыток ему удалось поставить свои классические опыты, хорошо известные сейчас. С помощью «генератора» и «резонатора» Герц экспериментально доказал (способом, который сегодня описывают во всех учебниках), что колебательный разряд вызывает в пространстве волны, состоящие из двух колебаний – электрического и магнитного, поляризованных перпендикулярно друг другу. Герц установил также отражение преломление и интерференцию этих волн, показав, что все опыты полностью объяснимы теорией Максвелла.
По пути, открытому Герцем, устремились многие экспериментаторы, но им не удалось многого прибавить у уяснению сходства световых и электрических волны, которую брал Герц (около 66 см.), они наталкивались на явления дифракции, затемнявшие все другие эффекты. Чтобы избежать этого, нужны были установки таких больших размеров, которые практически в те времена были нереализуемы. Большой шаг вперед сделал Аугусто Риги (1850-1920), которому с помощью созданного им нового типа генератора удалось возбудить волны длиной несколько сантиметров (чаще всего он работал с волнами длиной 10,6 см.). Таким образом, Риги удалось воспроизвести все оптические явления с помощью приспособлений, которые в основном являются аналогами соответствующих оптических приборов. В частности, Риги первому удалось получить двойное преломление электромагнитных волн. Работы Риги начатые в 1893 г. и время от времени описывавшиеся им в заметках и статьях, публиковавшихся в научных журналах, были затем объединены и дополнены в теперь уже ставшей классической книге «Оптика электрических колебаний», вышедшей в 1897 г., одно лишь название которой выражает содержание целой эпохи в истории физики.
В 1891 г. русский ученый П.Н. Лебедев начал работать в Московском университете в должности лаборанта. Но у Петра Николаевича был уже большой план научной работы.
Основные физические идеи этого плана были напечатаны П.Н. Лебедевым в Москве, в небольшой заметке «Об отталкивательной силе лучеиспускающих тел». Начиналась она словами: «Максвелл показал, что световой или тепловой луч, падая на поглощающее тело, производит на него давление в направлении падения…» Исследование светового давления стало делом всей, к сожалению короткой, жизни П.Н. Лебедева: последняя незаконченная работа этого великого экспериментатора тоже была посвящена давлению света.
Из теории Максвелла следовало, что световое давление на тело равно плотности энергии электромагнитного поля. (При полном отражении давление будет в два раза больше.) Экспериментальная проверка этого положения представляла большую трудность. Во-первых, давление очень мало и нужен чрезвычайно тонкий эксперимент для его обнаружения, не говоря уже о его измерении. И Лебедев создает свою знаменитую установку – систему легких и тонких дисков на закручивающемся подвесе. Это были крутильные весы с невиданной до тех пор точностью. Во-вторых, серьезной помехой был радиометрический эффект: при падении света на тело (тонкие диски в опытах Лебедева), оно нагревается. Температура освещенной стороны будет больше, чем температура теневой. Возникает дополнительная отдача, направленная в ту же сторону, что и световое давление, но во много раз превосходящая его. Кроме того, при наличии разности температур возникаю конвекционные потоки газа. Все это надо было устранить. П.Н. Лебедев с непревзойденным мастерством искуснейшего экспериментатора преодолевает эти трудности. Платиновые крылышки подвеса были взяты толщиной всего 0,1-0,01 мм, что приводило к быстрому выравниванию температуры обеих сторон. Вся установка была помещена в наивысший достижимый в то время вакуум (порядка 0,0001 мм рт. ст.). П.Н. Лебедев сумел сделать это очень остроумно. В стеклянном баллоне, где находилась установка, Лебедев помещал каплю ртути и слегка подогревал ее. Ртутные пары вытесняли воздух, откачиваемый насосом. А после этого температура в баллоне понижалась и давление оставшихся ртутных паров резко уменьшалось (ртутные пары, как говорят, замораживались).
Кропотливый труд увенчался успехом. Предварительное сообщение о давление света было сделано Лебедевым в 1899 г., затем о своих опытах он рассказал в 1900 г. в Париже на Всемирном конгрессе физиков, а в 1901 г. в немецком журнале «Анналы физики» была напечатана его работа «Опытное исследование светового давления». Работа получила высочайшую оценку ученых и стала новым, блестящим экспериментальным подтверждением теории Максвелла. В. Томсон, например, узнав о результатах опытов Лебедева, в беседе с К.А, Тимирязевым сказал: «Вы, может быть, знаете, что я всю жизнь воевал с Максвеллом, не признавая светового давления, и вот ваш Лебедев заставил меня сдаться перед его опытами». Ф. Пашен писал Лебедеву: «Я считаю Ваш результат одним из важнейших достижений физики за последние годы».
К впечатляющим словам этих физиков можно добавить еще то, что доказательство существования светового давления имело огромное философское и мировоззренческое значение. Ведь из факта существования давления электромагнитных волн следовал очень важный вывод о том, что они обладают механическим импульсом, а значит, и массой. Итак, электромагнитное поле обладает импульсом и массой, т.е. оно материально, значит, материя существует не только в форме вещества, но и в форме поля.
Date: 2015-05-18; view: 661; Нарушение авторских прав