Тепловое излучение. Закон Кирхгофа

Глава I

Тепловое излучение — это электромагнитное излучение, возбуждаемое за счет энергии теплового движения атомов и молекул. Если излучающее тело не получает теплоты извне, то оно охлаждается и его внутренняя энергия уменьшается. Тепловое излучение свойственно всем телам при температурах выше абсолютного нуля.

Если нагретое тело поместить в полость, ограниченную идеально отражающей (непроницаемой для излучения) оболочкой, то с течением времени установится статистическое равновесие: тело получает от поглощаемого излучения в единицу времени столько же энергии, сколько оно будет излучать само. При этом распределение энергии между телом и излучением с течением времени не изменяется. Устано­вившиеся в этой полости излучение, находящееся в статистическом равновесии с нагретым телом, есть равновесное тепловое излучение. Всякое другое излучение, возбуждаемое не нагреванием, а каким-либо иным способом, не приводит к установлению статистического равновесия. Например, если внутрь упомянутой выше полости поместить тело, светящееся благодаря предварительному облучению ультрафиолетовыми лучами, то свечение этого тела постепенно ослабнет и прекратится. Это произойдет потому, что поглощаемые телом лучи (находящиеся в полости благодаря отражению стенками оболочки) не способны вновь вызывать свечение тела. Таким образом, нетепловое излучение всегда неравновесно. Тепловое излучение иногда называют температурным.

При падении на поверхность какого-либо тела лучистого потока наблюдаются следующие явления:

а) часть потока отражается обратно в окружающее пространство. При этом происходит или зеркальное отражение, или поверхностное рассеяние потока в зависимости от структуры поверхности тела;

б) часть потока пройдет через тело;

в) остальная часть потока будет поглощена телом, а его энергия превратится в другие виды энергии.

Величина ρ, равная отношению лучистого потока Рρ, отраженного телом, к лучистому потоку Р, падающему на поверхность тела, называется коэффициентом отражения

Величина τ, равная отношению лучистого потока Р_τ, прошедшего через данное тело (среду), к лучистому потоку, падающему на данное тело (среду), называется коэффициентом пропускания

Коэффициент пропускания характеризует прозрачность тела (среды) по отношению к падающему излучению.

Величина α, равная отношению лучистого потока Р_α , поглощенного телом, к лучистому потоку, падающему на тело, называется коэффициентом поглощения тела

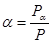
Из закона сохранения энергии следует, что

Рρ + Р_{τ +} Р_α = 1, поэтому ρ + τ + α = 1

Измерения показывают, что коэффициенты поглощения, пропускания и отражения тела зависят от длины волны λ, падающего излучения и от температуры тела, т. е.

α = f(λ,T); τ=φ(λ,T); ρ=F(λ,T).

Для монохроматичес­кого излучения они назы­ваются спектральными коэффициентами поглоще­ния, пропускания и отра­жения и обозначаются (для данной температуры тела) α_λ , ρ_λ, τ_λ

На рис. 1.1 графически изображена зависимость спектрального коэффициента поглощения некоторого тела от длины волны при данной температуре Т.

При изменении температуры характер кривой α = f(λ,T)) может измениться; лучи, сильно поглощающиеся при одной температуре, могут пропускаться при другом температуре, и наоборот.

Зависимость коэффициентов α, ρ и τ от длины волны является во многих случаях физической причиной окрашенности тел, не излучающих собственного света. Если, например, тело при освещении его белым светом имеет красный цвет, то его коэффициент поглощения τ для коротковолновой (зелено-фиолетовой) части видимого спектра близок к единице, а для длинноволновой — близок к нулю; соответственно коэффициент отражения этого тела для «красных» лучей близок к единице, а для «зелено-фиолетовых» — близок к нулю.

Цвет тела существенно зависит и от спектрального состава падающего на него света. При освещении упомянутого выше тела синим светом оно будет казаться почти черным, так как синие лучи ими почти полностью поглощаются. Окраска прозрачных тел также определяется зависимостью коэффициента пропускания от длины волны.

Например, вещество, сильно поглощающее все лучи, кроме синих, будет играть роль фильтра, выделяющего из белого цвета только синие лучи. Можно подобрать различные вещества, из которых одни пропускают только красные лучи (τ _кр 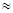0,8 0,9), другие — только синие (τ _син 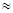0,8 0,9) и т. д., причем остальные лучи поглощаются. Такие вещества употребляются для изготовления светофильтров. Их вводят или прямо в состав стекла, или в слой желатины (или прозрачной пластмассы), которые помещаются между двумя обычными стеклами.

Тело, которое поглощает полностью все падающие на него излучения любой длины

волны при любой температуре, называют абсолютно черным (точнее абсолютно поглощающим) телом. Его коэффициент поглощения для всех длин волн при любых температурах равен единице.

Абсолютно черных тел в природе нет, но можно указать на тело, которое по своим свойствам практически не будет отличаться от абсолютно черного. Такой моделью абсолютно черного тела является полость с очень малым отверстием (рис. 1.2). Луч, (любой длины волны), попавший внутрь такой полости, может выйти из нее обратно только после многократных отражений. При каждом отражении от стенок полости часть энергии луча поглощается и лишь ничтожная доля энергии лучей, попавших в отверстие, сможет выйти обратно; поэтому коэффициент поглощения отверстия оказывается весьма близким к единице. Такая «модель» абсолютно черного тела может быть нагрета до высоких температур; тогда из отверстия в полости выходит интенсивное излучение и отверстие будет ярко светиться (при этом оно по-прежнему остается абсолютно поглощающим). Излучение абсолютно черного тела иногда называется «черным излучением», а само тело — «полным излучателем».

Топочное устройство с «глазком» в плавильных или коксовых печах, муфельные печи с отверстием, зрачок глаза являются примерами практических абсолютно черных тел.

Встречаются тела, для которых коэффициент поглощения меньше единицы, но не зависит от длины волны. Такие тела называются «серыми». Для них α выражается прямой, ордината которой меньше единицы (см. рис. 1.1).

Рассмотрим теперь лучеиспускание различных тел. Нагретые тела излучают энергию в виде электромагнитных волн различных длин (инфракрасные, видимые и ультрафиолетовые лучи и др.).

Количество R энергии, излучаемой с 1 м² поверхности тела за одну секунду по всем длинам волн, называется интегральной плотностью излучения.

Измерения показывают, что энергия излучения распределяется неравномерно между всеми длинами волн, которые испускаются нагретым телом. Разложим излучение нагретого тела в спектр и найдем энергии Δ R_λ приходящиеся на равные узкие участки спектра шириной Δ λ. Для этого можно перемещать вдоль спектра полоску зачерненной платины, которая, поглотив энергию излучения этого интервала, нагреется. Повышение же температуры может быть найдено по изменению ее сопротивления; такой прибор называется болометром.

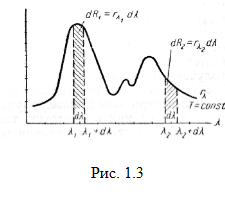
Можно также воспользоваться термопарой, которая позволяет измерять энергию поглощеного излучения по величине возникающей термоэлектродвижущей силы. Откладывая по оси ординат величину r_λT= Δ R/ Δ λ мы получим представление о распределении энергии по длинам волн нагретого тела. На рис. 1.3 показана сглаженная кривая, изображающая такое распределение.

Заштрихованная площадка, равная произведению r_λTdλ, показывает энергию излучения (с 1 м² поверхности тела за одну секунду), содержащуюся в участке спектра от длины волны λ до λ + dλ

dR _λ= r_λTdλ

Величина r_λT называется спектральной плотностью излучения тела и является функцией распределения энергии по спектру. Она выражает собой мощность излучения с 1 м² поверхности тела, приходящуюся на единичный интервал длин волн спектра вблизи данной волны λ..

Измерения показывают, что спектральная плотность излучения для данного тела зависит как от длины волны λ, вблизи которой взят интервал dλ, так и от температуры тела Т.

Очевидно, что интегральная плотность излучения тела связана со спектральной плотностью излучения соотношением

и на рис. 1.3 изображается площадью, заключенной между кривой r_λT и осью абсцисс.

Установлено, что испускательные и поглощательные спобности тел пропорциональны (например, сажа или платиновая чернь имеют большой коэффициент поглощения и большую плотность излучения; наоборот, полированное серебро обладает малым коэффициентом, поглощения и малой плотностью излучения). Эту пропорциональность можно показать, если внутрь нагретой полости (например, внутрь муфельной печи) внести фарфоровый черепок, часть которого зачернена тушью. Когда черепок нагреется и примет температуру полости, отличить темные места черепка от светлых, незачерненных, оказывается невозможным. Темные места больше поглощают, но и больше излучают, а светлые места меньше излучают, зато больше отражают. Вынув черепок из печи, мы заметим яркое свечение зачерненных мест, так как теперь они больше излучают, чем светлые места (отраженное излучение от них отсутствует, так как нет падающего излучения).

Получение света от пламени горящей свечи основано на той же пропорциональности между испускательной и поглощательной способностями тел. В пламени имеются частицы сажи, обладающие большим поглощением; они и дают яркий свет. Если пламя не содержит частиц сажи (например, пламя газовой горелки), оно не будет светиться.

Результаты экспериментальных исследований и термодинамические рассуждения привели к следующему утверждению (закон Кирхгофа):

для всех тел, независимо от их природы, отношение спектральной плотности излучения к спектральному коэффициенту поглощения при той же температуре и для тех же длин волн есть универсальная функция от длины волны и температуры.

Таким образом, за он Кирхгофа можно выразить равенством:

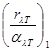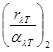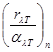= = … = = f(λ,T)

где индексы 1, 2,... относятся к первому, второму и т.д. телам. Допустим, что одно из этих тел — абсолютно черное. Обозначим его спектральную плотность излучения через u_λТ. Учитывая, что коэффициент поглощения абсолютно черного тела равен единице, можем написать закон Кирхгофа так:

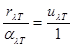= f(λ,T) (1.1)

Следовательно, универсальная функция Кирхгофа f(λ,T) есть спектральная плотность излучения абсолютно черного тела, т.е. f(λ,T) = u_λТ, поэтому:

отношение спектральной плотности излучения любого тела к его спектральному коэффициенту поглощения равно спектральной плотности излучения абсолютно черного тела для той же длины волны и при той же температуре.

Из формулы (1.1) следует, что r_λT=α_λТ и_λТ, а так как α_λТ < 1, то r_λT < и_λТ. Следовательно, тепловое излучение любого тела в любой области спектра всегда меньше, чем тепловое излучение абсолютно черного тела в этой же области спектра и при то же температуре.

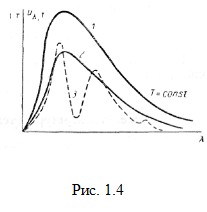На рис. 1.4 даны опытные кривые распределения энергии в спектре абсолютно черного тела 1, «серого» тела 2 и произвольного тела 3. Кривая спектрального распределения для серого тела может быть получена из кривой распределения для абсолютно черного тела путем умножения ординат последней на постоянный множитель, меньший единицы и равный коэффициенту поглощения серого тела. Таково приблизительно излучение вольфрамовой проволоки в электрических лампах.

Излучение некоторых тел является селективным (избирательным). Кривая излучения 3 таких тел может иметь несколько максимумов и минимумов, по вся она лежит ниже кривой излучения абсолютно черного тела, как следует из закона Кирхгофа.

Кроме дифференциальной формы закона Кирхгофа (1.1), существует его интегральная форма: отношение интегральной плотности излучения серых тел к их коэффициенту поглощения есть универсальная (общая для всех серых тел) функция температуры

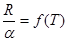(1.2)

где R и α относятся ко всему спектру излучения при данной температуре.

Для абсолютно черного тела α = 1 при всех температурах, поэтому f(Т) есть его интегральная плотность излучения при температуре Т.

Так как для всех тел α< 1, то их интегральное излучение всегда меньше, чем у абсолют черного тела. Это видно и на рис. 1.4, где площадь, ограниченная кривой излучения абсолютно черного тела, больше площади, ограниченной кривой излучения серого и любого другого тела.

Date: 2015-05-18; view: 1273; Нарушение авторских прав