
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Элементы квантовой механики
|
|
1. Главное квантовое число n определяет:
1) Импульс электрона
2) Орбитальный момент импульса электрона
3) Энергию атома
4) Импульс атома
5) Проекцию вектора момента импульса на направление магнитного поля
2. Орбитальное квантовое число l определяет:
1) Энергию атома
2) Орбитальный момент импульса электрона
3) Проекцию вектора орбитального момента импульса электрона на направление магнитного поля
4) Спин электрон
5) Проекцию спина на направление магнитного поля
3. Магнитное квантовое число m e определяет:
1) Орбитальный момент импульса электрона
2) Спин
3) Проекцию вектора момента импульса на направление магнитного поля
4) Проекцию спина на направление магнитного поля
5) Энергию электрона
4. Магнитное спиновое число ms определяет:
1) Собственный момент импульса электрона
2) Орбитальный момент импульса электрона
3) Энергию электрона
4) Импульс электрона
5) Проекцию спина на направление магнитного поля
5. Электрон в атоме водорода находится в 3 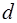 состоянии. При переходе атома в основное состояние, изменение орбитального момента импульса электрона равно (ħ):
состоянии. При переходе атома в основное состояние, изменение орбитального момента импульса электрона равно (ħ):
1) 2,45 2) 1,4 3) 1,05 4) 3,46 5) 0
6. Электрон в атоме водорода находится 3 р – состоянии. При переходе атома в основное состояние изменение орбитального момента импульс а электрона равно (ħ):
1) 3 2) 2 3) 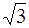 4)
4) 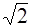 5) 0
5) 0
7. Момент импульса орбитального движения электрона, находящегося в S – состоянии, равен (Дж × с):
1) 1, 5 ×10 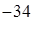 2) 1,06 × 10
2) 1,06 × 10 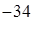 3)
3) 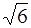 4)
4) 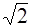 5) 0
5) 0
8. Вектор собственного магнитного момента электрона имеет в магнитном поле следующее число ориентаций (n, l, m – квантовые числа):
1) m 2) (2 l +1) 3) n 4) l 5) 2
9. При n =2 возможны следующие значения орбитального квантового числа l:
1) 3 2) 2 3) 1 4) – 2 5) –3
10. Максимальное число электронов, находящихся в состояниях, определяемых одним и тем же значением главного квантового числа n, равно:
1) (2 l +1) 2) 2(2 l +1) 3) 2 n 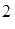 4) n
4) n 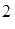 5) (n –1)
5) (n –1)
11. Максимальное число электронов, состояние которых определяется, одинаковыми квантовыми числами n, l, ml равно:
1) 4 2) 2 3) 1 4) (2 l +1) 5) Зависит от значения ml
12. Максимальное число электронов, состояние которых определяется, одинаковыми квантовыми числами n и l равно:
1) 1 2) (2 l +1) 3) 2(2 l +1) 4) n 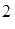 5) 2 n
5) 2 n 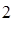
13. Электрон в атоме водорода находится в d – состоянии. Возможные проекции орбитального момента импульса электрона на направление магнитного поля равны:
1) 0, ħ, 2 ħ 2) 0, ħ, 2 ħ, 3 ħ 3) 0, 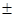 ħ
ħ  4) 0,
4) 0, 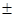 ħ,
ħ, 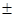 2 ħ 5) 0,
2 ħ 5) 0, 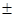 ħ,
ħ, 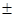 2 ħ,
2 ħ, 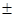 3 ħ
3 ħ
14. Орбитальный момент импульса электрона, находящегося в 4 d состоянии, равен (ħ):


1) 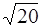 2)
2) 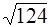 3)
3)  4)
4) 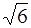 5) 2
5) 2
15. В состоянии 2 S могут находиться 2 электрона со следующими квантовыми числами n, l, m l, ms:
1) 2, 0, 0, 1/2 2) 1, 0, 0, + 1/2 3) 2, 1, 0, + 1/2
1, 0, 0, – 1/2 2, 0, 0, – 1/2 2, 0, 0, – 1/2
4) 2, 0, 0, + 1/2 5) 2, 0, 0, + 1/2
2, 0, 0, + 1/2 2, 0, 0, – 1/2
16. Заполненный электронный слой характеризуется квантовым числом n =3. В этом слое число электронов, имеющих одинаковое квантовое число m S = 1/2, равно:
1) 2 2) 8 3) 9 4) 12 5) 18
17. Заполненный электронный слой характеризуется квантовым числом n = 4. В этом слое число электронов, имеющих одинаковое квантовое число ml = – 2, равно:
1) 2 2) 8 3) 9 4) 12 5) 18
18. Заполненный электронный слой характеризуется квантовым числом n = 3. В этом слое число электронов, имеющих одинаковое квантовое число ml = – 3, равно:
1) 2 2) 8 3) 9 4) 6 5) 0
19. Заполненный электронный слой характеризуется квантовым числом n = 3. Число электронов в слое, которые имеют одинаковые квантовые числа m S = 1/2 и l = 2, равно:
1) 9 2) 5 3) 4 4) 2 5) 1
20. Максимальное число электронов, находящихся в L – слое, равно:
1) 2 3) 6 3) 8 4) 18 5) 32
21. Для электрона в состоянии lS возможен следующий набор квантовых чисел n, l, ml, ms:
1) 2, 0, 0, 1/2 2) 2, 0, 0, – 1/2 3) 1, 0, 0, 1/2
4) 2, 1, 0, – 1/2 5) 2, 1, 0, 1/2
22. Из указанных состояний электрон атома водорода обладает наименьшей энергией в случае:
1) 2 Р 2) 3 S 3) 4 S 4) 4 S, l =1 5) 4 S, l =2
чвыуц32
На рис. 9 приведены возможные ориентации вектора орбитального момента импульса электрона в магнитном поле:
 |
H H H H
2 ħ
ħ
0 0 0
-ħ - ħ
-2 ħ -2 ħ
1) 2) 3) 4)
Рис. 9
23. S – состоянию электрона соответствует рисунок:
1) 1 2) 2 3) 3 4) 4 5) Все четыре
24. Р – состоянию соответствует рисунок:
1) 1 2) 2 3) 3 4) 4 5) Все четыре
25. d – состоянию соответствует рисунок:
1) 1 2) 2 3) 3 4) 4 5) Все четыре
26. Электрон в атоме находится в S – состоянии. Наименьший угол, который может образовать вектор орбитального момента импульса электрона с направлением магнитного поля, равен:
1) 0° 2) 90° 3) arcsin 2/3 4) аrccos 2/3 5) аrctg 2/3
27. Наименьший угол, который может образовать с направлением магнитного поля вектор орбитального момента импульса электрона в состоянии 4 f, равен:
1) arccos 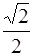 2) arccos
2) arccos 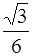 3) arcsin
3) arcsin 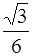
4) arctg 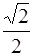 5) arctg
5) arctg 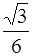
28. Электрон в атоме находится в P – состоянии. Наименьший угол, который может образовать вектор орбитального момента импульса электрона с направлением магнитного поля, равен:
1) 0° 2) 90° 3) aгсsin 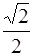 4) aгсsin
4) aгсsin 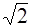 5) arccos
5) arccos 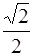

29. Электрон в атоме находится в d – состоянии. Наименьший угол, который может образовать вектор орбитального момента импульса электрона с направлением магнитного поля равен:
1) arcsin 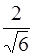 2) arctg 2/3 3) arcsin
2) arctg 2/3 3) arcsin 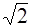
4) arссоs 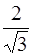 5) arccos
5) arccos 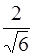
30. Из приведенных утверждений:
а) Магнитное квантовое число определяет энергию электрона в магнитном поле,
б) Спиновое квантовое число определяет проекцию спина на заданное направление,
в) Квадрат модуля 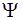 – функции определяет плотность вероятности нахождения частицы в той или иной точке пространства,
– функции определяет плотность вероятности нахождения частицы в той или иной точке пространства,
г) 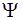 – функция – это вероятность нахождения частицы в той или иной точке пространства,
– функция – это вероятность нахождения частицы в той или иной точке пространства,
д)Существует одинаковая вероятность обнаружения микрочастицы в любой точке потенциального ящика.
Правильными являются:
1) Только а 2) а, б 3) Только г 4) Только д 5) б, в
31. Уравнение Шредингера для стационарных состояний имеет вид:
1) 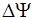 +
+ 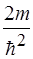 (Е + U)
(Е + U) 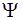 = 0 2)
= 0 2) 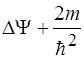 (Е – U
(Е – U 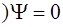
3) 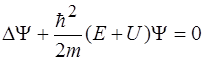 4)
4) 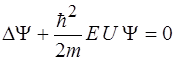
5) 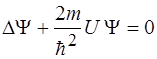
32. Уравнение Шредингера для атома водорода имеет вид:
1) 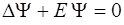 2)
2) 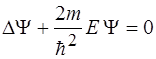
3) 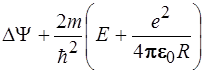
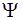 =0 4)
=0 4) 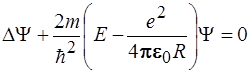
5) 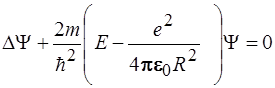
33. Стационарное уравнение Шредингера для гармонического осциллятора имеет вид:
1) 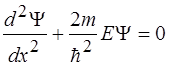 2)
2) 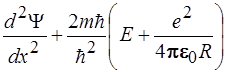
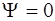
3) 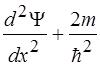
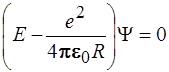 4)
4) 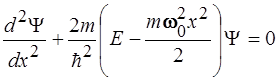
5) 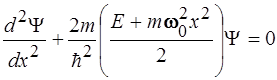
34. Одномерное временное уравнение Шредингера имеет вид:
1) i 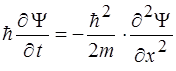 2)
2) 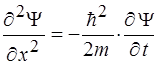 3)
3) 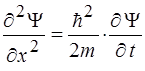
4) 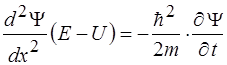 5)
5) 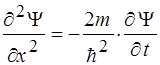

35. Стационарное уравнение Шредингера для свободной частицы имеет вид:
1) 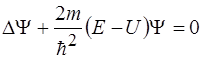 2)
2) 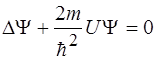 3)
3) 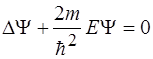
4)  5)
5) 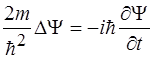
36. Для волновой функции 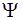 правильными являются следующие утверждения:
правильными являются следующие утверждения:
а) 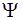 функция непрерывна и конечна,
функция непрерывна и конечна,
б) 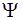 функция может принимать несколько значений,
функция может принимать несколько значений,
в) 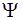 функция однозначна,
функция однозначна,
г) 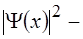 плотность вероятности обнаружить частицу в той или иной точке пространства,
плотность вероятности обнаружить частицу в той или иной точке пространства,
д) 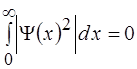 ,
,
е) 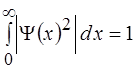 .
.
1)Только а 2) а, б 3)Только д 4) а, в, г, е 5)Все утверждения
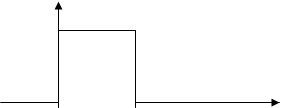
37. Частица с массой m и энергией Е подлетает к прямоугольному потенциальному барьеру высотой U 0, изображенному на рис. 10:
 U
U
 U 0
U 0
I II III
0 d x
Рис. 10
Для области 1 уравнение имеет вид:
1) 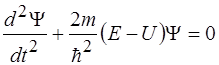

 2)
2) 
3) 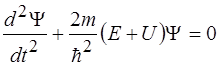 4)
4) 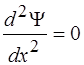 5)
5) 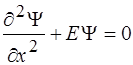
38. Частица с массой m и энергией Е подлетает к изображенному на рис. 10 прямоугольному потенциальному барьеру высотой U 0. Решение уравнения Шредингера для частицы, прошедшей сквозь барьер (область Ш на рис. 10) имеет вид 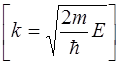 :
:
1) 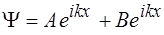 2)
2) 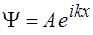 3)
3) 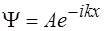 4)
4) 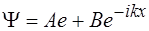 5) Не имеет решения
5) Не имеет решения
39. Частица с массой m и энергией Е подлетает к изображенному на рис. 10 прямоугольному потенциальному барьеру высотой U 0. Разность энергий (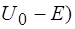 , при которой вероятность прохождения частицы сквозь барьер равна W, определяется выражением:
, при которой вероятность прохождения частицы сквозь барьер равна W, определяется выражением:
1) 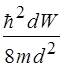 2)
2) 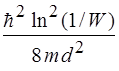 3)
3) 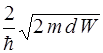
4) 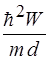 5)
5) 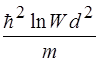
40. Если d – ширина барьера, U 0 – высота барьера, E – энергия микрочастицы, то вероятность туннельного эффекта для одной и той же микрочастицы наибольшая в случае:
1) 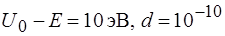 м 2) U 0 – E = 1эB, d =10
м 2) U 0 – E = 1эB, d =10 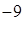 м
м
3) 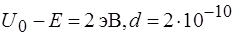 м 4) U 0 – E = 1эB, d =10
м 4) U 0 – E = 1эB, d =10 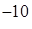 м
м
5) 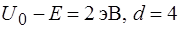 ·10
·10 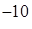 м
м
41. Электрон, протон, d – частица и молекула Н 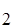 подлетают к одному и тому же потенциальному барьеру. Если энергия всех частиц одинакова, то вероятность прохождения сквозь барьер будет наибольшей для:
подлетают к одному и тому же потенциальному барьеру. Если энергия всех частиц одинакова, то вероятность прохождения сквозь барьер будет наибольшей для:
1) Электрона 2) Протона 3) 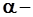 частицы
частицы
4) Молекулы Н 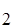 5) Для всех одинакова
5) Для всех одинакова
42. Электрон, длина волны Де – Бройля которого равна 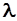
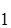 , двигаясь в направлении оси х, встречает на своем пути прямоугольный потенциальный барьер высотой U 0. Длина волны
, двигаясь в направлении оси х, встречает на своем пути прямоугольный потенциальный барьер высотой U 0. Длина волны 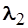 Де – Бройля электрона, прошедшего сквозь барьер определяется соотношением:
Де – Бройля электрона, прошедшего сквозь барьер определяется соотношением:
1) 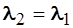
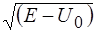 2)
2) 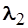
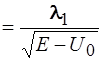 3)
3) 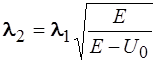
4) 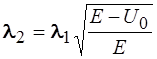 5)
5) 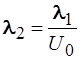
43. Состояние микрочастицы, движущейся в одномерной бесконечно глубокой потенциальной яме, описывается волновой функцией 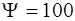 sin (2,5
sin (2,5 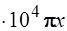 ). Микрочастица находится на энергетическом уровне:
). Микрочастица находится на энергетическом уровне:
1) Первом 2) Втором 3) Третьем 4) Четвертом 5) Пятом
44. Состояние микрочастицы массы m, движущейся в одномерной бесконечно глубокой потенциальной яме, описывается волновой функцией 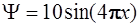 .Энергий этой микрочастицы может быть вычислена по формуле:
.Энергий этой микрочастицы может быть вычислена по формуле:
1) 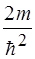 2)
2) 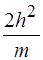 3)
3) 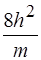 4)
4)  5) Она равна нулю
5) Она равна нулю
45. Микрочастица массы m в одномерном потенциальном ящике шириной l с бесконечно высокими стенками переходит с третьего уровня на первый. Энергия фотона, излучаемого при этом, определяется выражением:
1) 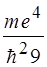 2)
2) 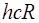
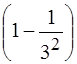 3)
3) 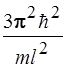 4)
4) 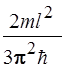 5)
5) 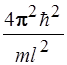
46. Состояние микрочастицы, движущейся в одномерной бесконечно глубокой потенциальной яме, описывается волновой функцией 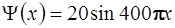 . Микрочастица находится на энергетическом уровне:
. Микрочастица находится на энергетическом уровне:
1) Первом 2) Втором 3) Третьем 4) Четвертом 5) Шестом
47. Частица в бесконечно глубокой одномерной потенциальной яме находится в состоянии 3 d. Плотность вероятности нахождения частицы минимальна в точках интервала (0 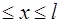 ):
):
а) 0 б) l в) l /3 г) 2 l/ 3 д) l/ 2 е) l/ 6
1) а, б 2) Только в 3) д, е 4) а, б 5) а, б, в, г
На рис. 11 приведены графики распределения вероятностей нахождения электрона в разных точках бесконечно глубокого одномерного потенциального ящика шириной l:

Рис. 11
48. Первому возбужденному состоянию электрона соответствует график на рис. 11:
1) 1 2) 2 3) 3 4) 4 5) Ни один не соответствует
49. Состоянию IS электрона соответствует график на рис. 11:
1) 1 2) 2 3) 3 4) 4 5) Ни один не соответствует
50. Состоянию 5 d электрона соответствует график на рис. 11:
1) 1 2) 2 3) 3 4) 4 5) Ни один не соответствует
51. Из приведенных на рис. 11 графиков наибольшей длине волны Де – Бройля микрочастицы соответствует график:
1) 1 2) 2 3) 3 4) 4
5) Длина волны Де – Бройля везде одинакова
52. Из приведенных на рис. 11 графиков наибольшей энергии микрочастицы соответствует:
1) 1 2) 2 3) 3 4) 4 5) Энергия везде одинакова
53. Состояние нейтрона в одномерной потенциальной яме с бесконечно высокими стенками описывается уравнением 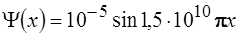 (м). Ширина потенциальной ямы равна (нм):
(м). Ширина потенциальной ямы равна (нм):
1) 200 2) 02 3) 2 4) 4 5) 4,2
54. Из приведенных утверждений:
а)Энергия микрочастицы в бесконечно глубокой потенциальной яме является величиной квантовой,
б) Вероятность прохождения частицы сквозь барьер не зависит от ее массы,
в) Существует отличная от нуля вероятность обнаружить частицу за пределами бесконечно глубокой потенциальной ямы,
г) Прозрачность потенциального барьера зависит от его толщины и высоты,
д) Вероятность обнаружения микрочастицы в середине бесконечно глубокой потенциальной ямы не зависит от ее энергии.
Правильными являются:
1) Только а 2) Только г 3) а, б 4) б, г 5) а, г
55. Энергия основного состояния квантового гармонического осциллятора равна:
1) 3/2 h 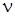 2) h
2) h 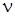 3) 1/2 h
3) 1/2 h 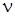 4) 1/3 h
4) 1/3 h 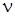 5) 0
5) 0
56. Математический маятник имеет длину 1 см. Если считать его квантовым осциллятором, то энергия нулевых колебаний этого маятника равна (Дж):
1) 1,6 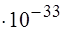 2) 3,2
2) 3,2 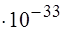 3) 0 4) 6,6
3) 0 4) 6,6 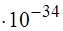 5) 3,3
5) 3,3 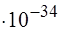
57. Электрон с энергией 10эВ, двигаясь вдоль положительной оси x, встречает на пути потенциальный прямоугольный барьер высотой 6 эВ. Длина волны Де – Бройля электронов при прохождении через этот барьер изменяется во столько раз:
1) 1,25 2) 0,8 3) 1,6 4) 2,5 5) 0,4
58. Протон с энергией 1 MэB изменил при прохождении потенциального барьера Де – Бройлевскую длину волны на 1 %. Высота потенциального барьера (в МэВ) равна:
1) 20000 2) 200 3) 250 4) 12 5) 12000
59. Частица в прямоугольном потенциальном ящике шириной l находится в первом возбужденном состоянии. Плотность вероятности нахождения частицы максимальна в точке интервала (0< x < l):
1) x = 0 2) х = 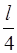 3) x =
3) x = 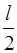 4) х = l 5) Везде одинакова
4) х = l 5) Везде одинакова
60. Частица в прямоугольном потенциальном ящике находится в невозбужденном состоянии. Ширина ящика l. Плотность вероятности нахождения частицы минимальна в точке интервала (0< x < l):
1) x = 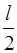 2) x =
2) x = 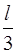 3) x =
3) x = 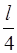 4) x = l 5) Везде одинакова
4) x = l 5) Везде одинакова
61. Электрон в атоме водорода находится на третьем энергетическом уровне. Возможные значения орбитального момента импульса электрона равны:
а) 0 б) 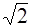
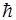 в)
в) 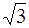
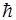 г)
г) 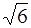
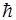
1) Только а 2) Только б 3) а, в 4) а, б, г 5) в, г
62. Энергия нулевых колебаний математического маятника, являющегося квантовым осциллятором, равна:
1) h 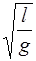 2) h
2) h 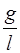 3)
3) 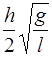 4)
4) 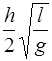 5) 2
5) 2 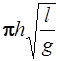
63. Электрон движется в одномерной бесконечно глубокой потенциальной яме, причем наименьшее расстояние между энергетическими уровнями, определяющими его состояние равно его средней кинетической энергии при температуре T. Это возможно при ширине ямы, равной:
1) 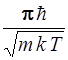 2)
2) 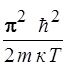 3)
3) 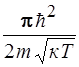 4)
4) 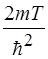 5)
5) 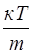
64. Математический маятник длиной 1cм, представляющий собой квантовой осциллятор, имеет энергию 2,4 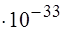 Дж. В каком энергетическом состоянии он находится?
Дж. В каком энергетическом состоянии он находится?
1) Первом 2) Втором 3) Нулевом 4) Третьем 5) Четвертом
65. Вероятность того, что электрон, движущийся в бесконечно глубокой потенциальной яме шириной l, находящийся в состоянии n =3, будет обнаружен в левой трети ямы, равна:
1) 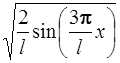 2)
2) 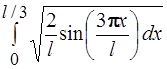
3) 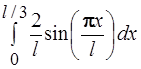 4)
4) 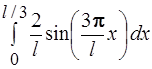 5) 0
5) 0
66.Вероятность того, что электрон, движущийся в бесконечно глубокой потенциальной яме шириной l, находящийся в состоянии n =2, будет обнаружен в середине ямы, равна:

1) 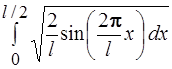 2)
2) 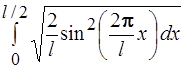
3) 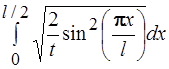 4)
4) 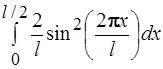 5) 0
5) 0
67. Отношение орбитальных моментов импульса электронов, находящихся в состоянии f и P, равно:
1) 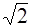 2)
2) 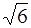 3)
3) 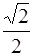 4)
4) 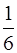 5) 1
5) 1
68. Отношение орбитальных моментов импульса электронов, находящихся в состоянии S и d, равно:
1) 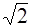 2)
2) 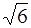 3)
3) 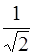 4)
4) 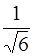 5) 0
5) 0
69. Отношение орбитальных моментов импульса электронов, находящихся в состоянии f и d, равно:
1) 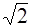 2)
2) 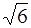 3)
3) 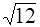 4)
4) 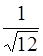 5) 1
5) 1
70. Энергия возбуждения атома водорода равна 12,09 эВ. Все возможные значения квадрата орбитального момента импульса электрона равны:
а) 0 б) 1 в) 2 г) 6 д) 12 1) а, б 2) б, в 3) а, в, г 4) в, г, д 5) а
Date: 2015-05-18; view: 2371; Нарушение авторских прав