Экспериментальные основы квантовой механики

Квантовая теория и статистическая физика

(Часть I)

Квантовая механика

Конспект лекций для студентов ЭКТ-2

Г.

Оглавление

§1. Экспериментальные основы квантовой механики.. 3

§2. Классическое и квантовое описание системы.. 4

[ §3.] Принцип неопределенности.. 5

[ §4.]Полный набор динамических переменных. 5

[ §5.] Постулаты квантовой механики.. 5

§6. Роль классической механики в квантовой механике. 6

[ §7.]Волновая функция и ее свойства. 6

[ §8.] Принцип суперпозиции состояний.. 6

§9. Понятие о теории представлений.. 7

[ §10.]Операторы в квантовой механике. 7

[ §11.]Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра. 8

§12. Среднее значение измеряемой величины.. 11

§13. Вероятность результатов измерения. 11

§14. Коммутативность операторов и одновременная измеримость физических величин (1/2*) 12

[ §15.] Операторы координаты 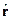, импульса 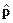, момента импульса 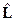, энергии 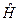. 13

§16. Решение задачи на собственные функции и собственные значения для оператора 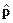... 13

§17. Решение задачи на собственные функции и собственные значения для оператора 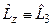. 15

§18. Вычисление коммутаторов, содержащих операторы (и 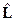*). 16

[ §19] Волновое уравнение. 18

§ 20 Производная оператора по времени.. 19

§ 21 Интегралы движения в квантовой механике. 20

§22. Флуктуации физических величин (1/2*) 20

§ 23. Неравенства Гайзенберга. (1/2*) 22

[ § 24.]Оператор Гамильтона различных систем.. 23

§ 25. Стационарное состояние различных систем.. 25

[ § 26.] Решение волнового уравнения в случае свободной материальной точки.. 25

§ 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы.. 27

[ § 28. ]Собственный механический момент (спин) 28

§ 29*. Операторы 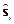и и 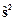их свойства. 29

§ 30. Спиновая переменная волновой функции.. 29

§ 31. Матрицы Паули (и их свойства)*. 30

§ 32. Принцип тождественности.. 32

§33. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения. 32

A.1. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближение. 36

A.2. Критерий применимости теории возмущений.. 37

A.3. Стационарная теория возмущений в случае близких энергетических уровней. 38

Экзаменационные вопросы по курсу "Квантовая теория". 41

Экзаменационные задачи по курсу "Квантовая теория". 42

Экзаменационные вопросы по курсу "Квантовая теория".(минимум) 43

Экзаменационные задачи по курсу "Квантовая теория".(минимум) 43

Решения задач по курсу "Квантовая теория". 44

Экспериментальные основы квантовой механики

1900г. Планк ввел понятие о квантах и ввел квантовую постоянную. Работа Планка объясняла теорию излучения твердых тел.

1905г. Классификация спектров Ритцем и Ридбергом. Все спектральные линии могут быть посчитаны через термы 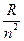, где 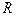- постоянная Ридберга, n – натуральное число.

1913г. Н. Бор теоретически объяснил спектр атома водорода (постулаты Бора).

Эксперименты Франка и Герца. Они рассматривали неупругое рассеяние электронов на атомах. Пропускали пучки электронов через пары ртути. При определенных энергиях, электроны при соударении с атомами ртути теряли часть своей энергии.

Установка:

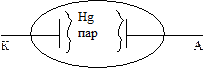
Была показана энергетическая дискретность атома ртути, определены энергетические уровни:

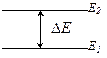
1922г. Опыты Штерна и Герлаха по расщеплению атомного пучка в неоднородном магнитном поле.

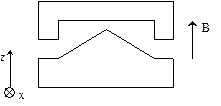
По оси z поле в обкладках магнита неоднородно. Так как есть градиент поля 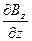, то если пропускать вдоль оси x частицы, имеющие магнитный момент 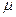, то возникает сила:

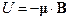
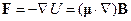
Наблюдалось расщепление атомного пучка. С точки зрения классической теории все равновероятны и поэтому должна получиться одна широкая полоса. Наблюдались две четкие линии.

Подтвердили, что магнитный момент атома квантуется, т. е. принимает дискретные значения.

,

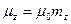где 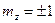для серебра.

1923 – 1924 гг. Теория Де Бройля корпускулярно-волнового дуализма частиц. Соотношения теории:

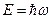
Здесь слева параметры частицы: энергия и импульс. Справа параметры волны: частота, волновой вектор.

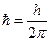
Волна Де Бройля:

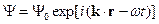
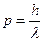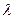, - длина волны Де Бройля.

1927г. Дэвиссон и Джермер. Рассеяние электронов на кристаллической решетке. Подтверждение волновых свойств частиц.

Date: 2015-05-18; view: 1438; Нарушение авторских прав