
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Елементарні частинки
|
|
Довідковий матеріал
· Повна енергія релятивіської частинки:
Е = m0c2 + Ек,
де m0c2 − енергія спокою частинки, Ек − кінетична енергія частинки.
· Закон збереження енергії для ядерних реакцій:
Σ m0c2 + Σ Ек= Σ m′0c2 + Σ Е′к,
де Σ m0c2 та Σ m′0c2 − відповідно сума енергій спокою частинок до та після реакції, Σ Ек та Σ Е′к − сума кінетичних енергій частинок до й після реакції.
· Імпульс релятивіської частинки:
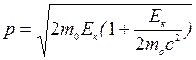 .
.
§ При розгляді зіткнення частинок часто використовують інваріантну величину:
Е 2 − р 2 с 2 = 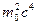 , де Е і р − повна енергія й імпульс системи, m 0− маса спокою утвореної частинки.
, де Е і р − повна енергія й імпульс системи, m 0− маса спокою утвореної частинки.
§ Значення порогової кінетичної енергії для налітаючої частинки т 1 на частинку-мішень т 2: 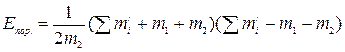 , де
, де 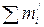 – сума мас частинок, утворених в результаті реакції.
– сума мас частинок, утворених в результаті реакції.
Задачі
5.465. Розганяючись прискорювальним полем у бетатроні, електрон набуває кінетичної енергії 0,8 МеВ. Яку швидкість має електрон? [2,75∙108 м/с].
5.466. Знайти швидкість протона, який у прискорювальному полі пройшов різницю потенціалів 500 МВ. [2,1∙108 м/с].
5.467. Знайти сумарну кінетичну енергію всіх частинок, які виникають у процесі розпаду вільного нейтрона за схемою: n → p + e −+ 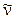 . Кінетичну енергію нейтрона і масу спокою антинейтрино можна не враховувати. [0,77 МеВ].
. Кінетичну енергію нейтрона і масу спокою антинейтрино можна не враховувати. [0,77 МеВ].
5.468. Показати, що народження пари електрон−позитрон одним квантом можливе тільки в тому разі, коли в реакції бере участь частинка з масою спокою m ≠ 0. [ (Е+m 1 c 2 ) 2 −p 2 c 2 =(m 1 = 2 m) 2 c 4, де p=E/c (після взаємодії вихідні частинки знаходяться в стані спокою на порозі реакції). Рівність не виконується при m 1=0].
5.469. Фотони з енергіями в 1,51 МеВ взаємодіють між собою з утворенням пари електрон−позитрон за схемою: 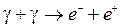 . Яку швидкість будуть мати утворені електрон і позитрон? [2,82∙108 м/с].
. Яку швидкість будуть мати утворені електрон і позитрон? [2,82∙108 м/с].
5.470. Покажіть, що при зіткненні фотона з вільним електроном він не може передати йому всю свою енергію. [Нехай фотон передає енергію електрону, тоді 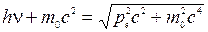 . Звідки
. Звідки 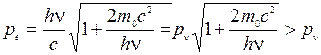 , що протирічить закону збереження імпульсу].
, що протирічить закону збереження імпульсу].
5.471. У камеру Вільсона, яка міститься в однорідному магнітному полі з індукцією 5 Тл, влітає електрон з кінетичною енергією 150 МеВ і залишає слід у вигляді дуги кола. Знайти радіус кривизни траєкторії електрона. [12,9 см].
5.472. При співударі електрона й позитрона з однаковими кінетичними енергіями 0,3 МеВ вони перетворюються у два однакових фотони. Чому дорівнює енергія утворених фотонів та яка довжина хвилі в них? [0,812 МеВ; 1,53 пм].
5.473. Середня швидкість зміни магнітного потоку в бетатроні на 80 МеВ складає 60 Вб/с. Визначити: 1) число обертів електрона орбітою за час прискорення; 2) шлях, пройдений електроном, якщо радіус орбіти дорівнює 0,3 м; 3) час прискорення. [1) 1,33∙106 обертів; 2) 2,5∙103 км; 3) 0,0083 с].
5.474. Позитрон з кінетичною енергією 0,75 МеВ налітає на вільний електрон, що перебуває у стані спокою. У результаті анігіляції виникає два γфотони з однаковими енергіями. Визначити кут φ між напрямками їхнього розлітання. [98о54/].
5.475. У циклотроні з радіусом дуантів 0,8 м та індукцією поля 1,5 Тл прискорюються протони. Визначити: 1) максимальну кінетичну енергію, якої набувають протони; 2) частоту генератора, який живить циклотрон (часом проходження протонами прискорювального проміжку знехтувати). [1) 68 МеВ; 2) 2,29∙107 Гц].
5.476. Фотон з енергією 3,02 МеВ у полі важкого ядра перетворився в пару електрон−позитрон. Беручи, що кінетична енергія частинок однакова, визначити кінетичну енергію кожної частинки. [0,998 МеВ].
5.477. Схема розпаду π0-мезона під час руху: π0→ γ + γ. Знайти кут між напрямками розлітання γквантів, якщо їхні енергії Е 1 та Е 2, а маса спокою π0-мезона дорівнює m 0. [ 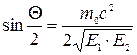 ].
].
5.478. Елементарна частинка 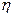 -мезон (
-мезон (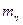 =0,589372 а.о.м.), розпадаючись, перетворюється у два однакових
=0,589372 а.о.м.), розпадаючись, перетворюється у два однакових 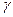 -фотони. Визначте енергію та довжину хвилі
-фотони. Визначте енергію та довжину хвилі 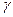 -фотонів. Кінетичну енергію і імпульс
-фотонів. Кінетичну енергію і імпульс 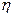 -мезона можна не враховувати. [
-мезона можна не враховувати. [ 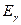 = 274,5 МеВ;
= 274,5 МеВ; 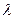 = 4,53 фм].
= 4,53 фм].
5.479. Бомбардуючи пучком заряджених  -мезонів нерухому водневу мішень, одержують
-мезонів нерухому водневу мішень, одержують 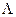 -гіперони і нейтральні
-гіперони і нейтральні 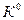 -мезони за схемою:
-мезони за схемою: 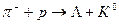 . Визначте порогову енергію цієї реакції. Врахуйте, що маси спокою
. Визначте порогову енергію цієї реакції. Врахуйте, що маси спокою 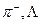 і
і 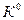 -частинок відповідно дорівнюють: 0,1449275 а.о.м., 1,1980676 а.о.м. і 0,53462158 а.о.м. [768,7 МеВ].
-частинок відповідно дорівнюють: 0,1449275 а.о.м., 1,1980676 а.о.м. і 0,53462158 а.о.м. [768,7 МеВ].
5.480. У циклотроні під дією магнітного поля і різниці потенціалів між дуантами в 30 кВ, 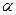 -частинки прискорюються до енергії 50 МеВ. Скільки обертів за час прискорення в циклотроні встигають зробити
-частинки прискорюються до енергії 50 МеВ. Скільки обертів за час прискорення в циклотроні встигають зробити 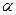 -частинки? На скільки відсотків збільшується маса
-частинки? На скільки відсотків збільшується маса 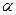 -частинки перед вильотом з циклотрону відносно маси її спокою? [ N = 416 обертів; маса збільшилася на 1,34%].
-частинки перед вильотом з циклотрону відносно маси її спокою? [ N = 416 обертів; маса збільшилася на 1,34%].
5.481. Схема розпаду нейтрального 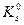 -мезона на два однакових
-мезона на два однакових 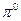 -мезони відбувається за схемою:
-мезони відбувається за схемою: 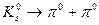 . Визначте кут між напрямами розлітання нейтральних
. Визначте кут між напрямами розлітання нейтральних 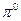 -мезонів, якщо маси спокою
-мезонів, якщо маси спокою 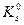 і
і 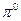 -мезонів відповідно дорівнюють 0,5346216 а.о.м. і 0,1449275 а.о.м. Кінетичну енергію і імпульс
-мезонів відповідно дорівнюють 0,5346216 а.о.м. і 0,1449275 а.о.м. Кінетичну енергію і імпульс 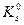 -мезона можна не враховувати. [
-мезона можна не враховувати. [ 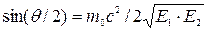 ;
; 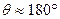 ].
].
5.482. Визначте власний час життя 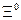 -гіперонів, які в нерухомій системі відліку пролітають від місця свого народження до місця розпаду відстань l = 0,70 м. Маса спокою і кінетична енергія цих частинок відповідно дорівнюють
-гіперонів, які в нерухомій системі відліку пролітають від місця свого народження до місця розпаду відстань l = 0,70 м. Маса спокою і кінетична енергія цих частинок відповідно дорівнюють  =2,3434
=2,3434 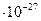 кг і Т = 9 ГеВ. [
кг і Т = 9 ГеВ. [ 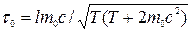 =
= 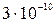 c].
c].
5.483. Визначте поріг фотонародження зарядженого 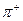 -мезона на нуклоні за такою схемою:
-мезона на нуклоні за такою схемою: 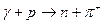 . Врахуйте, що маса спокою
. Врахуйте, що маса спокою 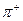 -мезона дорівнює 0,1502952 а.о.м. [
-мезона дорівнює 0,1502952 а.о.м. [ 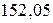 МеВ.]
МеВ.]
5.484. Власний час життя 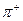 -мезонів, які розпадаються за схемою
-мезонів, які розпадаються за схемою 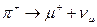 , дорівнює
, дорівнює 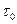 = 2,6
= 2,6 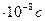 . Яку середню відстань пролітають ці мезони у нерухомій системі відліку від місця народження до точки їх розпаду, якщо їх кінетична енергія Т = 852,6 МеВ, а маса спокою
. Яку середню відстань пролітають ці мезони у нерухомій системі відліку від місця народження до точки їх розпаду, якщо їх кінетична енергія Т = 852,6 МеВ, а маса спокою  = 0,24889∙10−27кг. [
= 0,24889∙10−27кг. [ 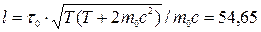 м].
м].
5.485. Під впливом слабких взаємодій 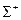 -гіперон розпадається за схемою:
-гіперон розпадається за схемою: 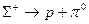 . Якою кінетичною енергією володітимуть як протон, так і
. Якою кінетичною енергією володітимуть як протон, так і 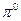 -мезон? Врахуйте, що маси спокою
-мезон? Врахуйте, що маси спокою 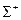 -гіперона і
-гіперона і 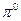 -мезона відповідно дорівнюють 1,27643586 а.о.м. і 0,1449275 а.о.м. Кінетичну енергію й імпульс
-мезона відповідно дорівнюють 1,27643586 а.о.м. і 0,1449275 а.о.м. Кінетичну енергію й імпульс 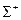 -гіперона можна не враховувати. [
-гіперона можна не враховувати. [ 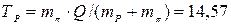 МеВ;
МеВ; 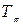 =101,23 МеВ]ю
=101,23 МеВ]ю
5.486. Визначте порогову кінетичну енергію бомбардуючого протона в реакції народження пари нуклон-антинуклон 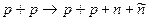 . [5,64 ГеВ].
. [5,64 ГеВ].
5.487. У сучасному синхрофазотроні з жорстким фокусуванням протони прискорюють до кінетичної енергії Т = 76 ГеВ. У скільки разів збільшується релятивістська маса протонів на виході із синхрофазотрона порівняно із його масою спокою? [82 рази].
5.488. Володіючи кінетичною енергією в 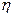 = 1,551 разів більшою за енергію спокою,
= 1,551 разів більшою за енергію спокою, 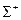 -гіперон пролітає в нерухомій системі відліку від місця народження до точки розпаду за схемою
-гіперон пролітає в нерухомій системі відліку від місця народження до точки розпаду за схемою 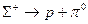 відстань 5,63 см. Визначте середній час руху гіперона в нерухомій системі відліку, прийнявши, що його маса спокою
відстань 5,63 см. Визначте середній час руху гіперона в нерухомій системі відліку, прийнявши, що його маса спокою  = 2,11378
= 2,11378 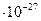 кг. [
кг. [ 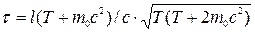 = 2,04
= 2,04 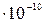 c].
c].
5.489. Для одержання 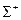 -гіперонів використовують реакцію зіткнення протон-протон за схемою
-гіперонів використовують реакцію зіткнення протон-протон за схемою 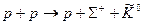 . Встановіть, які саме закони збереження дотримані в цій реакції? Визначте мінімальну кінетичну енергію налітаючого протона, необхідну для здійснення вказаної реакції. Врахуйте, що маси спокою
. Встановіть, які саме закони збереження дотримані в цій реакції? Визначте мінімальну кінетичну енергію налітаючого протона, необхідну для здійснення вказаної реакції. Врахуйте, що маси спокою 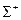 і
і 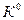 частинок відповідно дорівнюють 1,27643586 а.о.м. і 0,53462158 а.о.м. [1,796 ГеВ].
частинок відповідно дорівнюють 1,27643586 а.о.м. і 0,53462158 а.о.м. [1,796 ГеВ].
5.490. Нейтральний 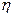 -мезон, розпадаючись, перетворюється на три однакових нейтральні
-мезон, розпадаючись, перетворюється на три однакових нейтральні 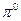 -мезони. Визначте кінетичну енергію кожної з частинок, що утворились після розпаду. Маси спокою
-мезони. Визначте кінетичну енергію кожної з частинок, що утворились після розпаду. Маси спокою 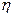 -мезона і
-мезона і 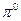 -мезона відповідно дорівнюють 0,589372 а.о.м. і 0,1449275 а.о.м. Кінетичну енергію й імпульс
-мезона відповідно дорівнюють 0,589372 а.о.м. і 0,1449275 а.о.м. Кінетичну енергію й імпульс 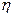 -мезона можна не враховувати. [48 МеB].
-мезона можна не враховувати. [48 МеB].
5.491. У фазотроні з радіусом дуантів 3 м протони розганяють до енергії 680 МеВ. Визначте індукцію магнітного поля в фазотроні. У скільки разів маса протонів в кінці прискорення у фазотроні буде більшою за його масу спокою? [1,26 Тл; 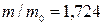 ].
].
5.492. Визначте порогову кінетичну енергію бомбардуючих протонів в реакції одержання трьох нуклон-антинуклонних пар (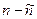 ) за схемою
) за схемою 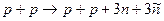 . [28,213 ГеВ].
. [28,213 ГеВ].
5.493. Яку відстань пролітають 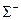 -гіперони від місця народження до точки розпаду в нерухомій системі відліку, якщо їх власний час життя
-гіперони від місця народження до точки розпаду в нерухомій системі відліку, якщо їх власний час життя 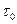 = 1,5∙10−10 c. Прийняти до уваги, що маса спокою цих частинок
= 1,5∙10−10 c. Прийняти до уваги, що маса спокою цих частинок  = 2,13314∙10−27 кг, а кінетична енергія дорівнює 8,85 ГеВ. [0,38 м].
= 2,13314∙10−27 кг, а кінетична енергія дорівнює 8,85 ГеВ. [0,38 м].
5.494. Яку порогову кінетичну енергію повинні мати бомбардуючі  -мезони в реакції за схемою
-мезони в реакції за схемою 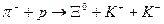 , щоб одержати нейтральні
, щоб одержати нейтральні 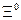 -гіперони? Чому дорівнює енергія реакції? Врахуйте, що маси спокою частинок
-гіперони? Чому дорівнює енергія реакції? Врахуйте, що маси спокою частинок 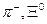 і
і 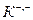 відповідно дорівнюють 0,1502952 а.о.м., 1,41170156 а.о.м. і 0,53032743 а.о.м. [
відповідно дорівнюють 0,1502952 а.о.м., 1,41170156 а.о.м. і 0,53032743 а.о.м. [ 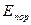 =2,21 ГеВ; Q = =1,225 ГеВ].
=2,21 ГеВ; Q = =1,225 ГеВ].
5.495. Яку енергію повинен мати 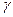 -фотон, щоб при його взаємодії з нерухомим нейтроном за схемою
-фотон, щоб при його взаємодії з нерухомим нейтроном за схемою 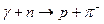 , народилися протон і
, народилися протон і  -мезон з сумарною кінетичною енергією 100 МеВ? Яку довжину хвилі має
-мезон з сумарною кінетичною енергією 100 МеВ? Яку довжину хвилі має 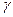 -фотон? Врахуйте, що маса спокою
-фотон? Врахуйте, що маса спокою  -мезона дорівнює 0,1502952 а.о.м. [
-мезона дорівнює 0,1502952 а.о.м. [ 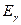 = 238,6 МеВ;
= 238,6 МеВ; 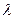 = 5,21 фм].
= 5,21 фм].
5.496. Протон, пройшовши у лінійному прискорювачі різницю потенціалів та набув кінетичної енергії 5 МеВ. Яку швидкість має протон на виході з лінійного прискорювача? [ 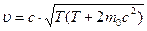 /(Т +
/(Т +  )= =
)= =  м/с].
м/с].
5.497. Високоенергетичний протон, зіткнувшись з нерухомою водневою мішенню у реакції за схемою 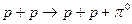 , породжує нейтральний
, породжує нейтральний 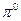 -мезон. Яку найменшу кінетичну енергію повинен мати у цьому випадку бомбардуючий протон? Врахуйте,що маса спокою
-мезон. Яку найменшу кінетичну енергію повинен мати у цьому випадку бомбардуючий протон? Врахуйте,що маса спокою 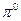 -мезона дорівнює 0,1449275 а.о.м. [279,7 МеВ].
-мезона дорівнює 0,1449275 а.о.м. [279,7 МеВ].
5.498. Визначте кінетичну енергію 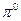 -мезона, в якого після розпаду за схемою
-мезона, в якого після розпаду за схемою 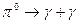 народилися два
народилися два 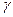 -фотони з однаковими енергіями, а кут між напрямками їх руху складає
-фотони з однаковими енергіями, а кут між напрямками їх руху складає 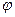 = 51,7º. Прийміть до уваги, що фотони розлітаються симетри чно відносно напрямку руху
= 51,7º. Прийміть до уваги, що фотони розлітаються симетри чно відносно напрямку руху 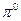 -мезона, в якого маса спокою дорівнює 0,2406∙10−27 кг. [175 МеВ].
-мезона, в якого маса спокою дорівнює 0,2406∙10−27 кг. [175 МеВ].
5.499. Після народження 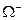 -гіперон, володіючи кінетичною енергією 6,73 ГеВ, пролетів у нерухомій системі відліку до точки розпаду відстань 19,2 см. Визначте власний час життя
-гіперон, володіючи кінетичною енергією 6,73 ГеВ, пролетів у нерухомій системі відліку до точки розпаду відстань 19,2 см. Визначте власний час життя 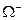 -гіперона, прйнявши, що його маса спокою дорівнює 2,972444∙10−27 кг. [
-гіперона, прйнявши, що його маса спокою дорівнює 2,972444∙10−27 кг. [ 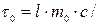
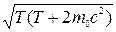 = 1,3
= 1,3 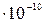 c].
c].
5.500. Додатньо заряджена частинка розганяється у фазотроні з радіусом дуантів 3 м та індукцією магнітного поля 1,54 Тл до такої енергії, що її відношення до маси частинки в цей момент 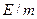 = 1,65∙1016 Дж/кг. Визначте, про яку частинку йде мова, якщо відомо, що її маса за час прискорення зросла на 22,5%. [ q/m= 4,81∙107 Кл/кг; це −
= 1,65∙1016 Дж/кг. Визначте, про яку частинку йде мова, якщо відомо, що її маса за час прискорення зросла на 22,5%. [ q/m= 4,81∙107 Кл/кг; це − 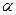 -частинка].
-частинка].
Date: 2015-05-18; view: 895; Нарушение авторских прав