
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Классические интерференционные схемы. Бипризма Френеля. Зеркала Френеля
|
|
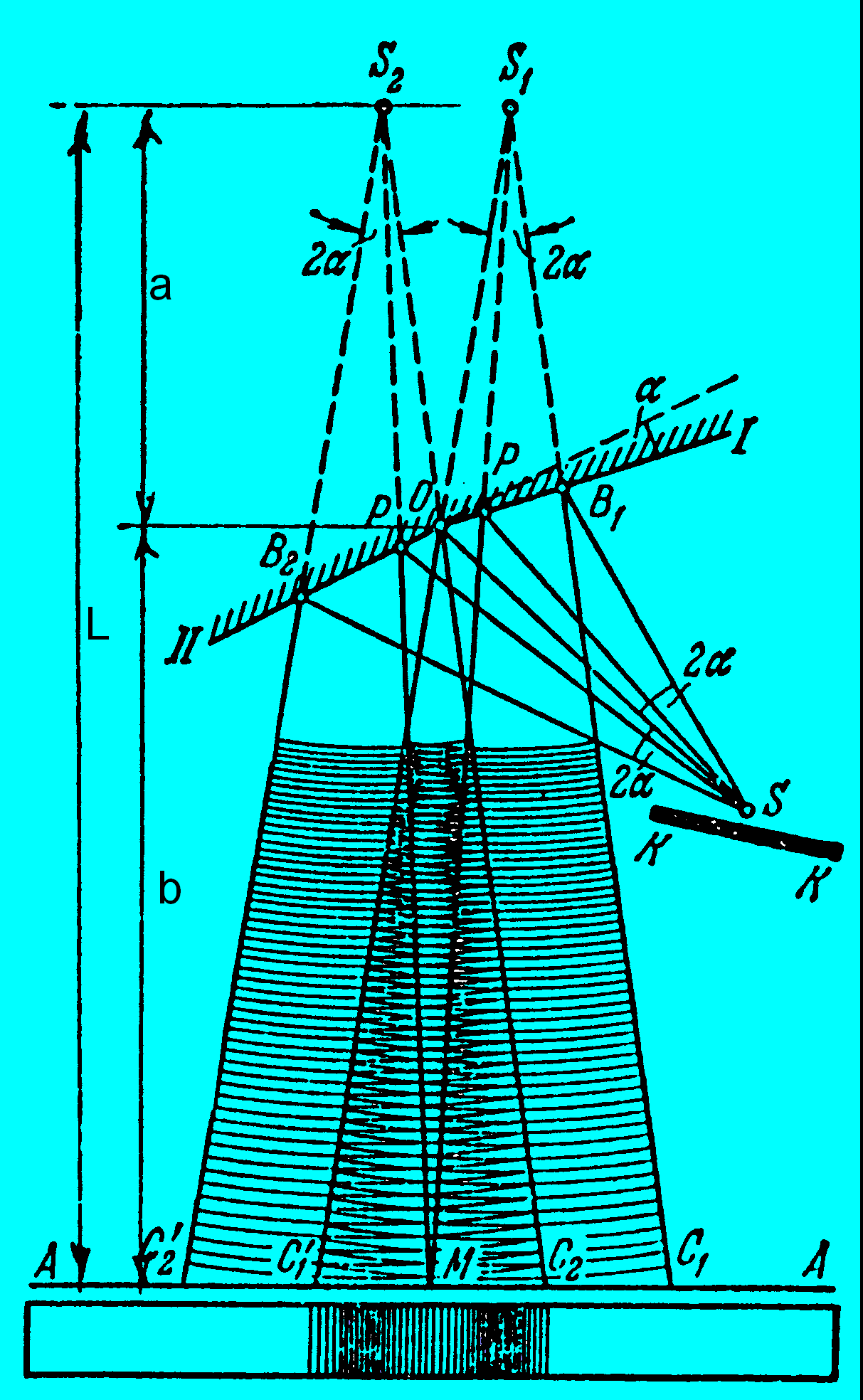 Бизеркала Френеля. Два плоских соприкасающихся зеркала располагаются так, что их отражающие поверхности образуют угол, близкий к 180°. Источник света (например, узкая светящаяся щель) помещается параллельно линии пересечения зеркал на расстоянии OS =
Бизеркала Френеля. Два плоских соприкасающихся зеркала располагаются так, что их отражающие поверхности образуют угол, близкий к 180°. Источник света (например, узкая светящаяся щель) помещается параллельно линии пересечения зеркал на расстоянии OS = 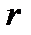 от неё. Вспомогательный экран КК преграждает свету путь от источника S к экрану АА.
от неё. Вспомогательный экран КК преграждает свету путь от источника S к экрану АА.
Источниками когерентных волн 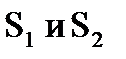 служат два мнимых изображения источника света S. Мнимые источники
служат два мнимых изображения источника света S. Мнимые источники 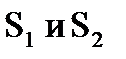 взаимно когерентны, исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрытия. (Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше 2 α). На основании законов отражения S и
взаимно когерентны, исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрытия. (Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше 2 α). На основании законов отражения S и 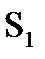 расположены относительно зеркала I симметрично, длина отрезка
расположены относительно зеркала I симметрично, длина отрезка 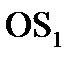 равна OS, т. е.
равна OS, т. е. 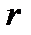 . Аналогично относительно зеркала II
. Аналогично относительно зеркала II 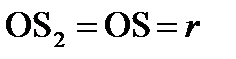 . Поэтому расстояние между источниками
. Поэтому расстояние между источниками 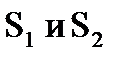 равно
равно 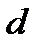 = 2
= 2 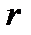 sin α ≈ 2
sin α ≈ 2 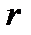 α.
α.
Расстояние от мнимых источников до линии пересечения зеркал
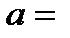
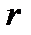 cos α ≈
cos α ≈ 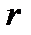 . Следовательно, L =
. Следовательно, L = 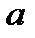 +
+ 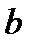 , где
, где 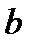 – расстояние от линии пересечения зеркал O до экрана АА.
– расстояние от линии пересечения зеркал O до экрана АА.
Расстояние  =
= 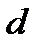 тем меньше и, следовательно, интерференционная картина тем крупнее, чем меньше угол между зеркалами α.
тем меньше и, следовательно, интерференционная картина тем крупнее, чем меньше угол между зеркалами α.
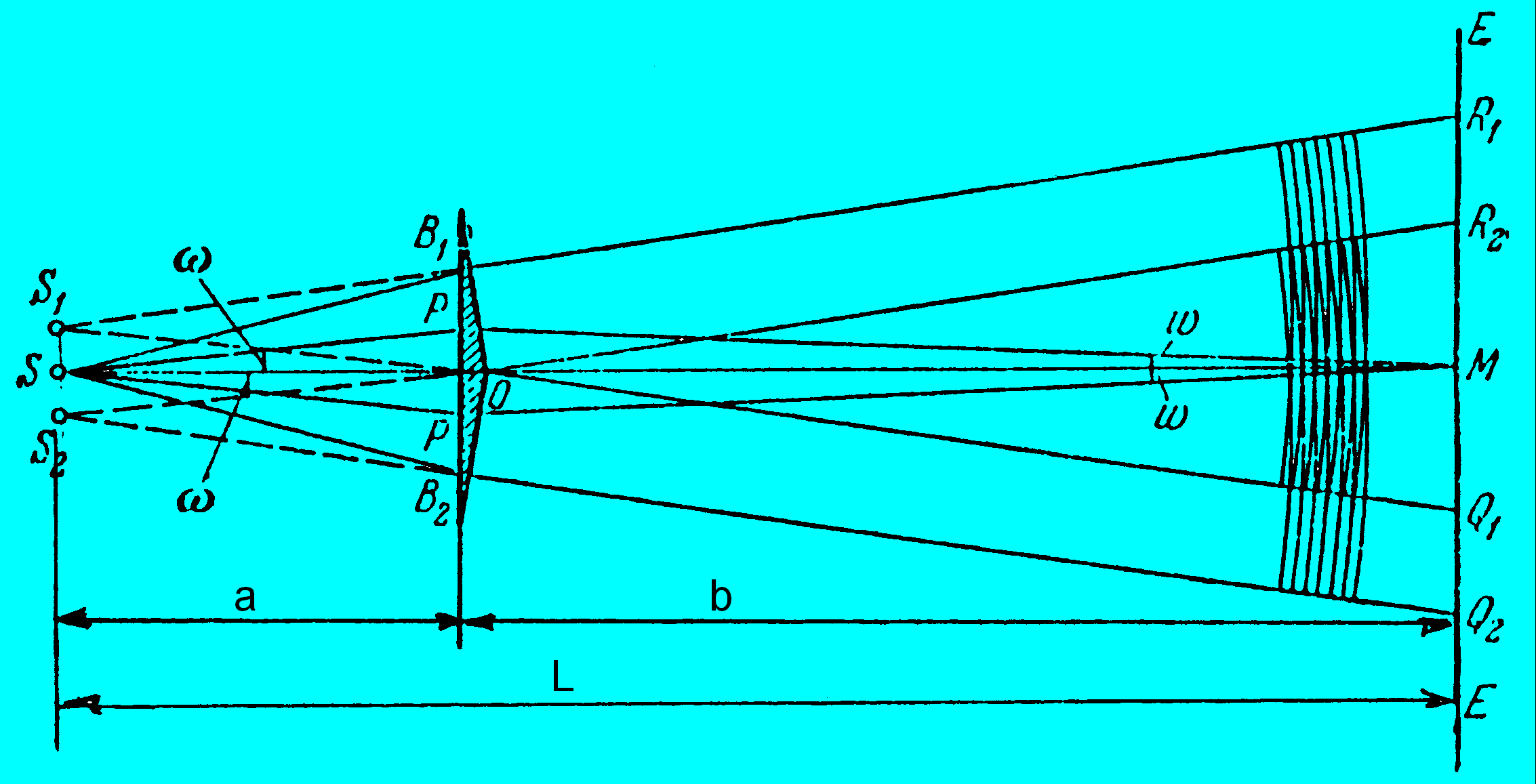 Бипризма Френеля состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами
Бипризма Френеля состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами 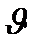 (порядка нескольких минут). Параллельно этому основанию на расстоянии
(порядка нескольких минут). Параллельно этому основанию на расстоянии 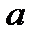 от него располагается источник света S. Свет от источника преломляется в обеих призмах, в результате чего за бипризмой распространяются световые пучки, как бы исходящие из мнимых источников
от него располагается источник света S. Свет от источника преломляется в обеих призмах, в результате чего за бипризмой распространяются световые пучки, как бы исходящие из мнимых источников 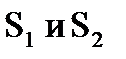 , являющихся когерентными. На экране происходит наложение когерентных световых пучков и наблюдается интерференция.
, являющихся когерентными. На экране происходит наложение когерентных световых пучков и наблюдается интерференция.
Так как преломляющий угол бипризмы 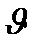 очень мал и малы углы падения световых лучей на бипризму, можно считать, что углы отклонения лучей
очень мал и малы углы падения световых лучей на бипризму, можно считать, что углы отклонения лучей 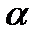 , падающих на верхнюю и нижнюю половинки бипризмы малы, а мнимые изображения источника света и сам источник расположены практически в одной плоскости:
, падающих на верхнюю и нижнюю половинки бипризмы малы, а мнимые изображения источника света и сам источник расположены практически в одной плоскости: 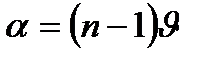 . Расстояние между источниками равно
. Расстояние между источниками равно 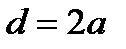 sin
sin 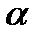
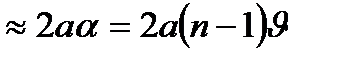 .
.
Расстояние от источников до экрана: 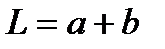 . Для наблюдения широких полос интерференции необходимо обеспечить малое расстояние
. Для наблюдения широких полос интерференции необходимо обеспечить малое расстояние 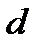 =
= 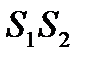 , при этом поле интерференции оказывается малым.
, при этом поле интерференции оказывается малым.
Date: 2015-05-18; view: 1564; Нарушение авторских прав