Интерференция света, интенсивность при суперпозиции двух монохроматических волн

Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.^[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них неортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

При интерференции энергия волн перераспределяется в пространстве.^[1] Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.

При наложении некогерентных волн средняя величина квадрата амплитуды результирующей волны равна сумме квадратов амплитуд накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий ее колебаний, обусловленных всеми некогерентными волнами в отдельности.

Электромагнитная волна называется монохроматической, если переменные поля меняются со временем по гармоническому закону. Для плоской монохроматической волны

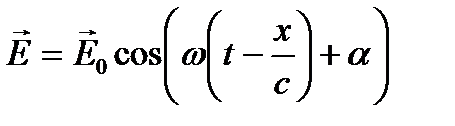. (9.8)

Здесь 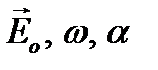- амплитуда, циклическая частота и начальная фаза, соответственно. Начальную фазу удобно сразу принять за нуль (выбор начала отсчета времени). Введем волновое число 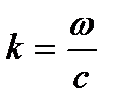. Тогда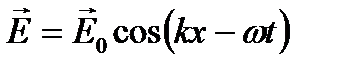

Если ввести волновой вектор 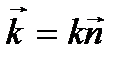, то последнюю формулу можно представить в виде: 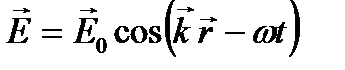. (9.12)

Последняя формула описывает волну, распространяющуюся в произвольном фиксированном направлении, которое задается единичным вектором .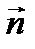

Для плоской монохроматической линейно поляризованной волны окончательно имеем: .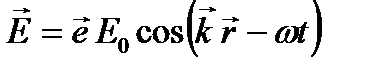

В общем случае плоская монохроматическая волна (9.12) представляет собой суперпозицию двух линейно поляризованных волн:

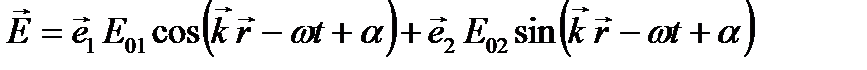. (9.14)

Здесь векторы 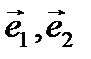- постоянные векторы перпендикулярные друг другу и перпендикулярные направлению распространению волны (т.е. вектору ).

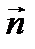Пусть волна распространяется вдоль оси 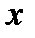. Далее, предположим, что вектор 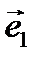направлен вдоль оси 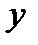, а вектор 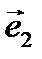направлен вдоль оси 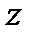. Тогда

.

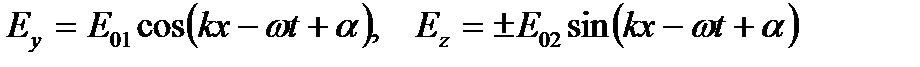Исключая из двух последних равенств время, найдем .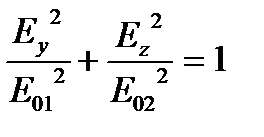

Последнее равенство показывает, что в плоскости 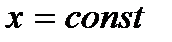вектор 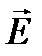вращается так, что его конец описывает эллипс. Поскольку распространение электромагнитной волны происходит в направлении оси 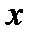, то изменение вектора 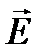в пространстве и во времени представляется в виде движения его конца по эллиптической спирали (эллиптически поляризованная волна). Шаг спирали равен длине волны 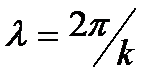. Если амплитуды равны по величине, то волна будет поляризована по кругу. Если одна из амплитуд равна нулю, то волна линейно поляризована. В общем случае плоская монохроматическая волна поляризована эллиптически

Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A ².

Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:

(*)

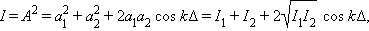
где Δ = r ₂ – r ₁ – так называемая разность хода.

Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = m λ (m = 0, ±1, ±2,...). При этом I _max = (a ₁ + a ₂)² > I ₁ + I ₂. Интерференционный минимум (темная полоса) достигается при Δ = m λ + λ / 2. Минимальное значение интенсивности I _min = (a ₁ – a ₂)² < I ₁ + I ₂. На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.

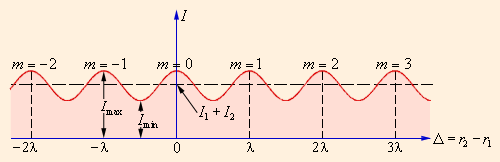Рисунок 3.7.4. Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума

В частности, если I ₁ = I ₂ = I ₀, т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид: I = 2 I ₀(1 + cos k Δ). В этом случае I _max = 4 I ₀, I _min = 0.

Date: 2015-05-18; view: 1385; Нарушение авторских прав