Линейный гармонический осциллятор. Система, совершающая одномерное колебательное движение под действием квазиупругой силы F = -kx, называется линейным гармоническим осциллятором (ЛГО)

Система, совершающая одномерное колебательное движение под действием квазиупругой силы F = -kx, называется линейным гармоническим осциллятором (ЛГО). Примерами таких систем служат пружинный, физический и математический маятники.

Потенциальная энергия ЛГО изменяется по закону

,

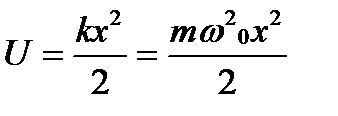где k = mω²₀ – коэффициент квазиупругой силы, ω₀ – собственная циклическая частота ЛГО, ω₀ = 2πν, ν – частота колебаний ЛГО, m – масса колеблющейся системы (частицы).

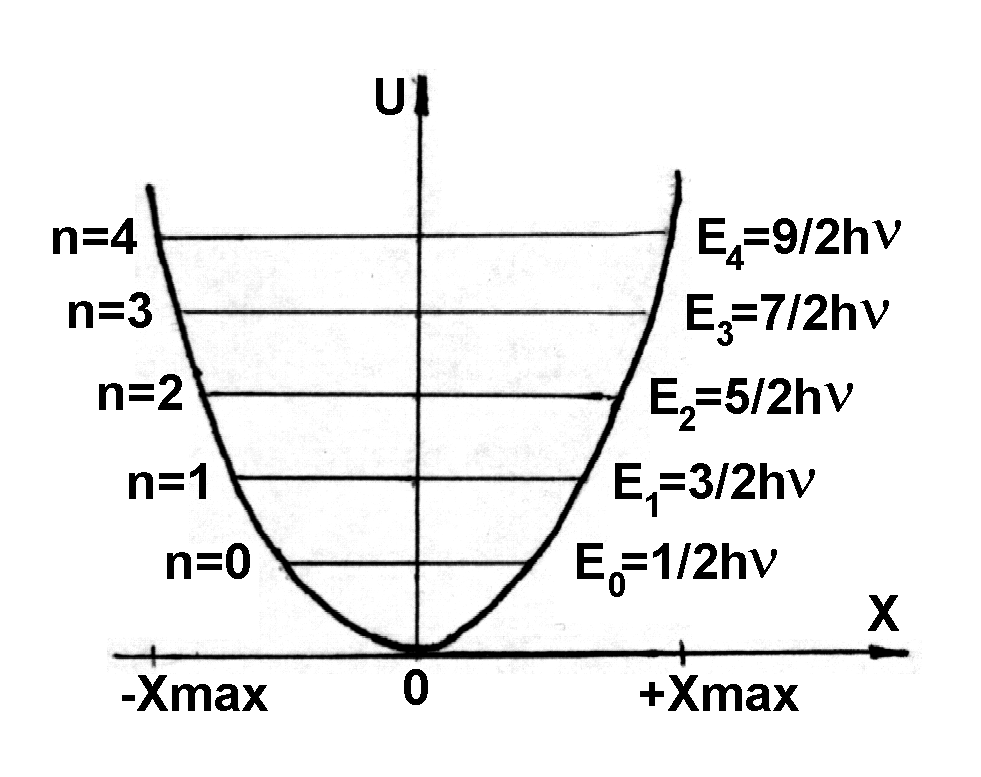
Амплитуда колебаний ЛГО определяется его полной энергией Е. В точках с координатами ±x_max полная энергия Е равна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (-x_max, +x_max). Таким образом, классический осциллятор находится в “потенциальной яме” c координатами -x_max ≤ х ≤ + x_max, ограниченной параболой на рис. 170.

Стационарное состояние ЛГО в квантовой механике определяется уравнением Шредингера вида

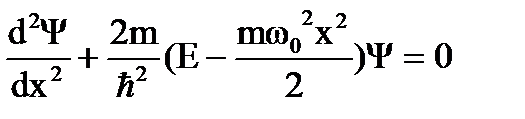
В теории дифференциальных уравнений доказано, что решение такого уравнения имеет место лишь при значениях Е, удовлетворяющих равенству

.

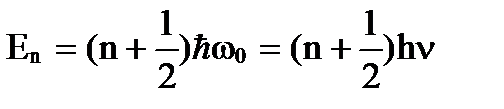Эта энергия называется собственным значением энергии ЛГО.

Выражение Е_n показывает, что: 1) энергия ЛГО квантуется; 2) уровни энергии находятся на одинаковом расстоянии друг от друга ΔЕ = hν 3) снизу энергия ограничена отличным от нуля (в отличие от прямоугольной “потенциальной ямы”) минимальным значением энергии Е₀ = (1/2)hν. Эта энергия называется энергией нулевых колебаний, является типичной для квантовых систем, и представляет собой прямое следствие соотношения неопределенностей. В самом деле, “падение на дно ямы” связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопределенность координаты частицы становится сколь угодно большой, что противоречит пребыванию частицы в “потенциальной яме”.

Вывод о наличии нулевой энергии ЛГО противоречит выводам классической теории, согласно которой наименьшая энергия, которую может иметь осциллятор, равна нулю, т.е. при Т = 0 энергия колебательного движения атомов кристалла должна обращаться в нуль. Следовательно, должно исчезнуть и рассеяние света, обусловленное колебаниями атомов.

Однако эксперимент показывает, что интенсивность рассеяния света при понижении температуры не равна нулю, а стремится к некоторому предельному значению, указывающему на то, что при Т → 0 колебания атомов в кристалле не прекращаются. Это подтверждает наличие нулевых колебаний.

4) строгое решение задачи о ЛГО показывает, что частицу можно обнаружить за пределами дозволенной области |x| ≤ x_max.

Существует отличная от нуля вероятность W обнаружить частицу в той области, которая является классически запрещенной (рис. 171). Это объясняется возможностью прохождения частицы сквозь потенциальный барьер.

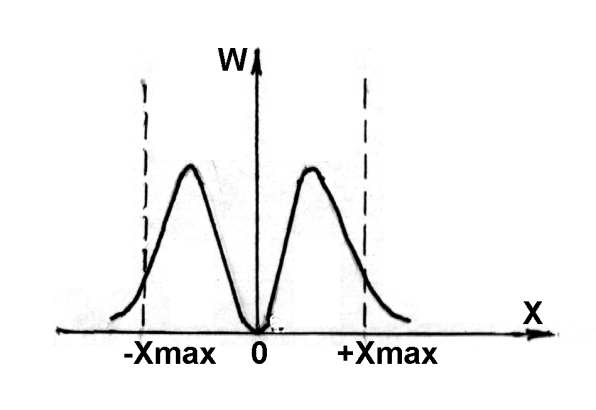
Рис. 171

Date: 2015-05-17; view: 775; Нарушение авторских прав