Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Соотношение неопределенностей Гейзенберга
|
|
Если электрон, или любая другая частица, ведет себя аналогично волне, то возникает вопрос: как определить их точное положение в пространстве? Для расчета движения частицы необходимо знать ее положение в пространстве (координату) и состояние движения (импульс).
В 1927 г. Гейзенберг теоретически пришел к выводу, что одновременное точное определение этих величин для элементарной частицы невозможно. Этот вывод можно записать аналитически в виде неравенства
,
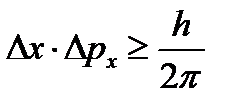где Δх – неопределенность координаты частицы, Δpх - неопределенность проекции импульса на ось х.
Это утверждение носит название соотношения неопределенностей Гейзенберга. Неопределённость данных величин связана не с несовершенством измерительной аппаратуры, а с объективными свойствами исследуемого объекта, т.е. с законом природы.
Поясним соотношение неопределенностей следующим примером.
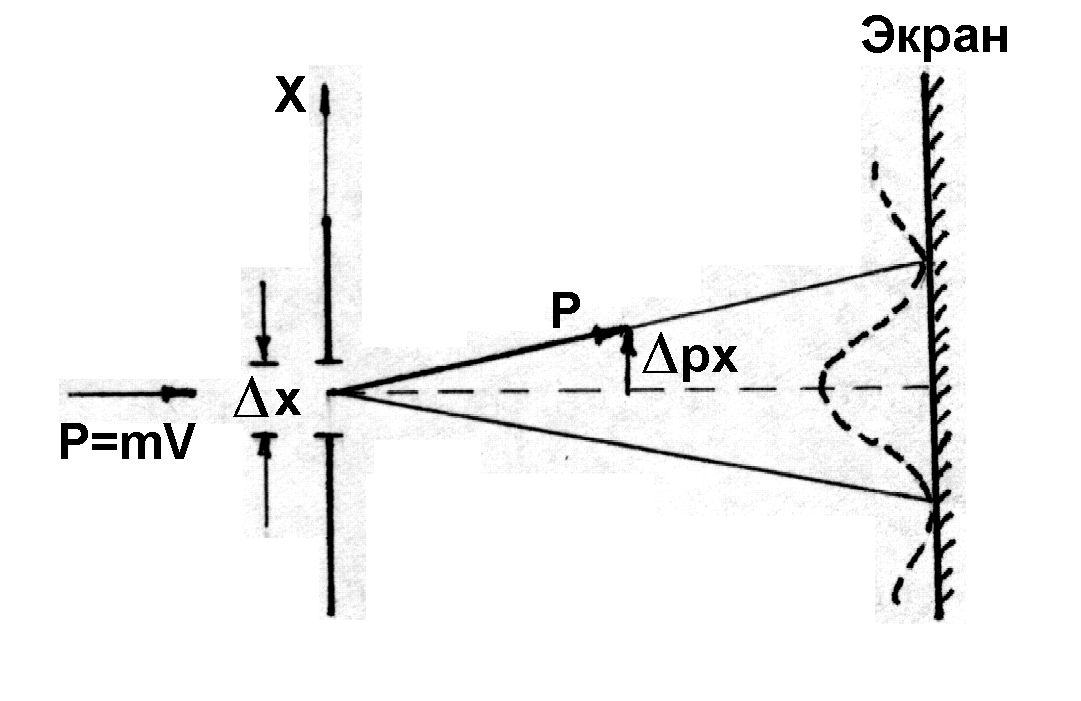
Пусть электрон летит в пучке ему подобных со скоростью v (рис. 165), его импульс p = m v. На пути электронного пучка поместим щель шириной Δх, расположенную перпендикулярно к направлению движения частицы. За щелью расположен экран, на котором наблюдается дифракционная картина. До прохождения частицы через щель ее составляющая импульса pх имеет точное значение равное нулю (щель по условию перпендикулярна импульсу), так что Δpх = 0, зато координата х является совершенно неопределенной. В момент прохождения частицы через щель положение меняется. У координаты х появляется вполне очевидная неопределенность Δх равна ширине щели, но это достигается ценой утраты определенности значения pх.
|
| Рис. 165 |
Действительно, вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла 2φ, где φ – угол, соответствующий первому дифракционному минимуму (при дифракции на одной щели интенсивностью максимумов высшего порядка можно пренебречь). Таким образом, появляется неопределенность Δpх = p·sinφ. Краю центрального дифракционного максимума (первому минимуму) от щели Δх соответствует угол φ, для которого из условия минимумов при дифракции на щели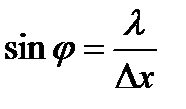 
. Следовательно, 
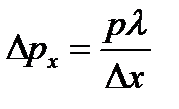, откуда получается соотношение
.
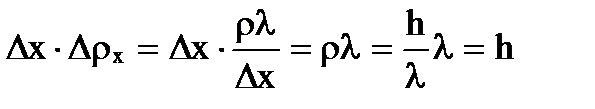Если учесть наличие максимумов высшего порядка, то неопределенность в определении импульса увеличивается и последнее выражение можно переписать
.
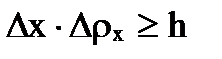Соотношение неопределенностей Гейзенберга имеет место для времени t и энергии Е:
. 
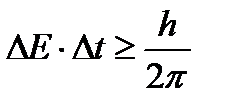Date: 2015-05-17; view: 829; Нарушение авторских прав