Туннельный эффект. Рассмотрим другой пример решения квантово-механической задачи – прохождение частицы сквозь потенциальный барьер

Рассмотрим другой пример решения квантово-механической задачи – прохождение частицы сквозь потенциальный барьер.

Пусть на пути частицы, перемещающейся только по оси х (одномерное движение, рис. 169) находится потенциальный барьер прямоугольной формы

высотой U (U – значение потенциальной энергии) и шириной l.

Граничные условия задачи можно записать в виде:

U(x) = 0 при x < 0,

U(x) = U при 0 ≤ x ≤ l,

U(x) = 0 при x > l.

При таких условиях задачи классическая частица, обладающая энергией Е, либо беспрепятственно пройдет над барьером при Е > U, либо отразится от него при Е < U и будет двигаться в противоположном направлении, т.е. она не может проникнуть сквозь барьер.

Исходя из квантовых представлений для микрочастицы даже при Е > U имеется отличная от нуля вероятность того, что частица отразится от барьера и будет двигаться в обратную сторону, а при Е < U имеется вероятность того, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Такая способность микрочастиц названа туннельным эффектом.

Подобные, казалось бы парадоксальные выводы, следуют непосредственно из решения уравнения Шредингера для условий данной задачи.

Для областей 1 и 3 эти уравнения имеют вид:

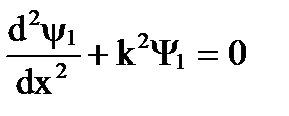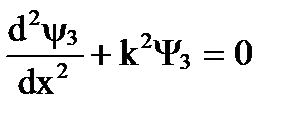; , где .

Для области 2:

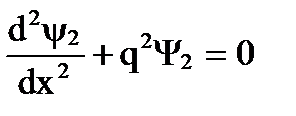, где .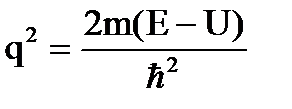

Общие решения этих дифференциальных уравнений

, ,

,

,

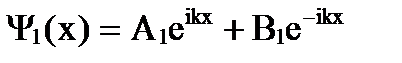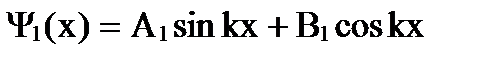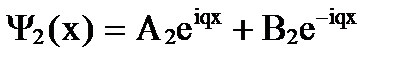
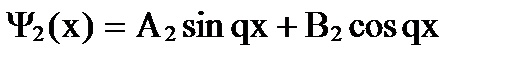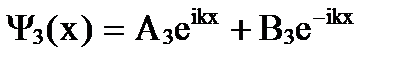
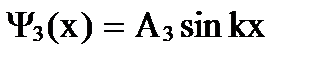т.е. все три функции представляют собой волны. В 1-й области - это две волны, движущиеся в противоположных направлениях, в 3-й области – одна волна, движущаяся слева направо (поэтому В₃ = 0). Качественный вид функции дан на рис. 167. Функции Ψ₁(х) и Ψ₃(х) имеют вид волн де Бройля, но с разными амплитудами. Волновая функция внутри барьера также не равна нулю. Из этого следует, что частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер.

Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера. Он определяется как отношение плотности потока прошедших сквозь барьер частиц к плотности потока падающих. Можно показать, что 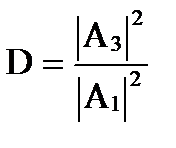. Аналитическое выражение коэффициента прозрачности

,

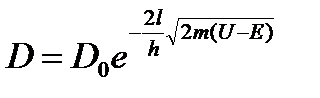где U – высота потенциального барьера; Е – энергия частицы; l – ширина барьера; D₀ –постоянный множитель, близкий к 1.

Видно, что D сильно зависит от массы частицы m, ширины барьера l и от (U – Е). Чем шире барьер, тем меньше вероятность прохождения частицы сквозь него.