Статистическое описание равновесных состояний

При рассмотрении основного уравнения МКТ принималось, что молекулы имеют различные скорости теплового движения. Если даже предположить, что в какой-то момент времени скорости всех молекул одинаковы по модулю и различны только по направлению, то соударения между молекулами приведут к изменению их скоростей и нарушению равенства скоростей по модулю.

Закон распределения по скоростям теплового движения молекул газа, находящегося в состоянии термодинамического равновесия, впервые был найден Максвеллом и называется распределением Максвелла.

Для получения этого распределения вводится трёхмерное пространство скоростей, в котором по взаимно ортогональным осям координат отложены компоненты υ_x; υ_y; υ_z скоростей молекул.

Пусть dN – число молекул в единице объёма газа, модули скоростей которых заключены в пределах от υ до (υ +dυ).

Очевидно, что концы векторов скоростей этих молекул должны лежать в пространстве скоростей внутри шарового слоя, имеющего объём

.

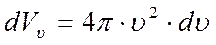При тепловом движении из-за его беспорядочности все направления скоростей молекул равновероятны. Поэтому число 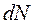должно быть пропорционально как числу 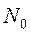молекул в единице объёма газа, так и объёму 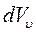шарового слоя и ещё должно зависеть от модуля скорости 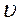, как какая-то функция 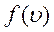. Таким образом

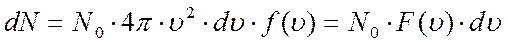, где

.

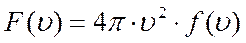Функция 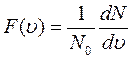представляет собой долю молекул, модули скоростей которых находятся в шаровом слое единичной толщины, а произведение

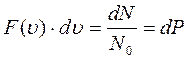
есть вероятность того, что модуль скорости молекулы заключён между 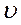и .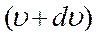

Ф ункция 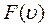называется функцией распределения молекул газа по модулям их скоростей.

Из физического смысла функции 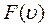следует, что

.

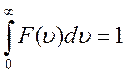Сложные расчёты показали, что

.

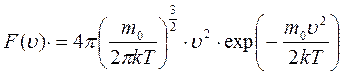Вся площадь, ограниченная кривой 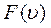и осью абсцисс, равна единице.

Кривая 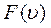описывает распределение молекул по модулям скоростей.

Используя выражение для 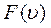можно записать закон распределения молекул по скоростям (закон Максвелла)

.

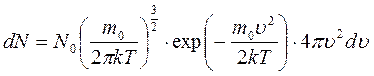Из этого закона можно определить так называемую наиболее вероятную скорость 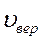соответствующую максимуму на графике :

.

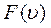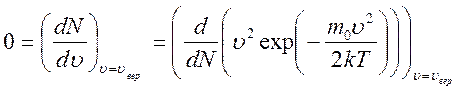Решение этого уравнения даёт:

.

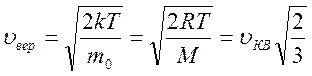Закон распределения молекул по скоростям позволяет вычислить и среднюю арифметическую скорость <υ> поступательного движения молекул идеального газа. Для этого необходимо долю молекул 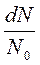, обладающих некоторой скоростью υ, умножить на эту скорость и проинтегрировать по всем скоростям от 0 до 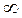, учитывая, что :

.

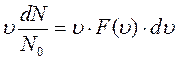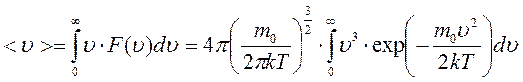В результате интегрирования получаем:

.

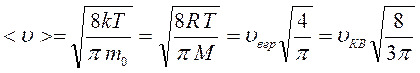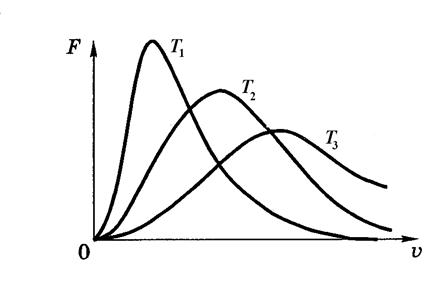
С увеличением температуры (Т ₃ > T ₂ > T ₁) максимум функции F (υ) смещается в сторону больших скоростей. При этом доля молекул, обладающих малыми скоростями, уменьшается, а доля молекул с большими скоростями увеличивается. Площадь под всеми тремя кривыми остаётся равной единице.

Аналогично закону распределения молекул по скоростям можно найти закон распределения молекул идеального газа по кинетическим энергиям их теплового движения. Это распределение устанавливает долю 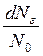молекул, кинетическая энергия которых 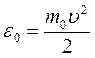заключена в интервале от 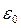до 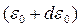. Чтобы получить такое распределение нужно в законе Максвелла перейти от скорости 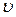к энергии 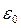по соотношениям 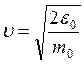и .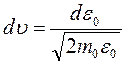

В результате получаем

.

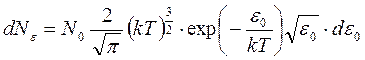Введём обозначение 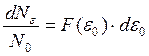, где

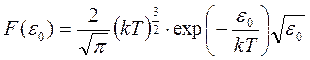– функция распределения молекул идеального газа по кинетическим энергиям.

По аналогии со средней скоростью найдём среднюю кинетическую энергию поступательного движения молекулы идеального газа:

.

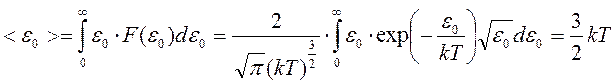Таким образом 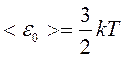, что и следовало ожидать.

Прямые измерения скоростей теплового движения молекул были впервые выполнены в 1920 г. Штерном в опытах с молекулярными пучками спустя 60 лет после опубликования закона Максвелла.

В качестве исследуемого газа были взяты пары серебра, которое испарялось в вакууме с поверхности платиновой проволоки, нагреваемой электрическим током..

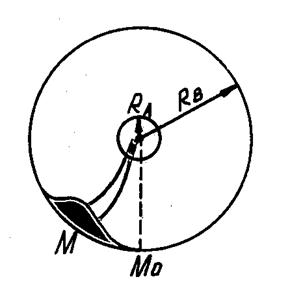На пути атомов серебра ставился цилиндрический экран радиусом 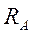с узкой щелью. Атомы серебра, пролетевшие сквозь щель, осаждались на стенке второго цилиндра радиуса 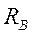, образуя узкую полоску 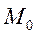. Если весь прибор вращать вокруг оси, совпадающей с платиновой проволокой, то атомы серебра попадут на стенки цилиндра 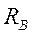в новое место .

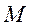По смещению полоски и известной угловой скорости вращения прибора можно было вычислить скорость движения атомов серебра

, где 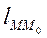– длина дуги .

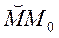Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по МКТ.

Зависимость толщины слоя серебра от места конденсации атомов пропорциональна зависимости атомов в этом месте от их скорости.

Опыт Штерна хорошо согласовался с распределением молекул по скоростям Максвелла.

Date: 2015-05-09; view: 1078; Нарушение авторских прав