Барометрическая формула. Молекулы любого газа, как и любые материальные точки всегда находятся в поле тяготения Земли

Молекулы любого газа, как и любые материальные точки всегда находятся в поле тяготения Земли. Если бы не было теплового движения молекул атмосферного воздуха, то все они упали бы на Землю. Если бы не было тяготения, то атмосферный воздух рассеялся бы по всей Вселенной.

Для определения закона изменения давления идеального газа с высотой в однородном поле тяготения будем считать, что газ находится в состоянии термодинамического равновесия, так, что его температура Т всюду одинакова. Выделим на высоте y = h столб газа высотой dy и площадью основания S.

Давление газа на нижнее основание столба равно р, а на верхнее основание – (р +dp). С учётом гидростатического давления ρgdy столба газа получаем

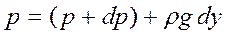или .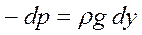

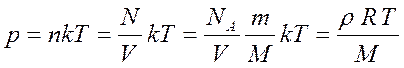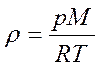
Так как то и

.

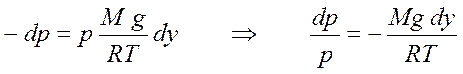Обозначив давление у поверхности Земли – р ₀ получаем после интегрирования

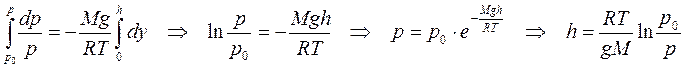
Два последних выражения называют барометрическими формулами, позволяющими определить высоту над поверхностью Земли по показаниям барометра.

Так как 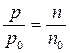то .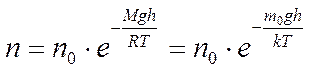

Если учесть, что 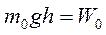– потенциальная энергия молекулы в однородном поле тяготения вблизи поверхности Земли (при условии, что на поверхности Земли 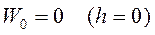) то можно записать

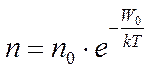
Эта формула является математическим выражением весьма общего и важного закона – Закона Больцмана для распределения частиц во внешнем потенциальном поле независимо от его физической природы.

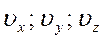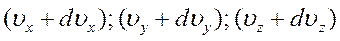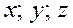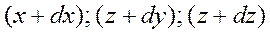Объединив распределения Максвелла и Больцмана получают Закон Максвелла-Больцмана, согласно которому число молекул, компоненты скорости которых лежат в пределах от до , а координаты – в пределах от до равно

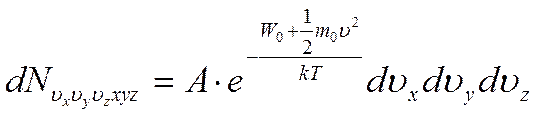где

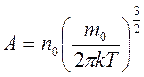– нормировочный множитель;

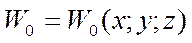и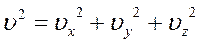

Date: 2015-05-09; view: 768; Нарушение авторских прав