Энтропия и вероятность

Термодинамической величиной, характеризующей направление протекания самопроизвольных термодинамических процессов, является энтропия. Наиболее вероятному равновесному состоянию соответствует максимум энтропии.

Пусть имеется сосуд объёмом V ₀, внутри которого находится одна молекула. Вероятность того, что частица будет обнаружена внутри некоторого объёма V < V ₀, выделенного внутри сосуда, равна 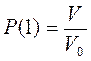. Если в сосуде находится не одна, а две частицы, то вероятность их одновременного обнаружения в указанном объёме определяется как произведение вероятностей нахождения в этом объёме каждой из частиц:

.

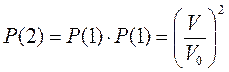Для N частиц вероятность их одновременного обнаружения в объёме V составит

.

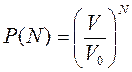Если в этом сосуде выделить два объёма V ₁ и V ₂ то можно записать отношения вероятностей того, что все молекулы находятся в указанных объёмах:

.

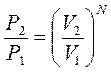Определим приращение энтропии в изотермическом процессе

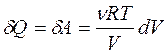
расширения идеального газа от V ₁ до V ₂:

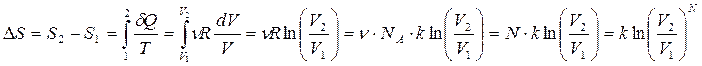
Используя отношение, вероятностей получаем:

.

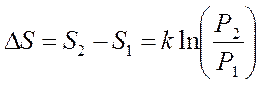Полученное выражение не определяет абсолютное значение энтропии в каком-либо состоянии, а только даёт возможность найти разность энтропий в двух различных состояниях.

Для однозначного определения энтропии используют статистический вес G, значение которого выражается целым положительным числом и пропорционально вероятности: G ~ P.

Статистическим весом макросостояния называется величина, численно равная количеству равновесных микросостояний, с помощью которых может быть реализовано рассматриваемое макросостояние.

Переход к статистическому весу позволяет записать соотношение для энтропии в виде формулы Больцмана для статистической энтропии:

.

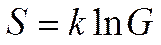Date: 2015-05-09; view: 765; Нарушение авторских прав