
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Поглощение света 3 page
|
|
Следовательно, перемножением матриц трансляции и преломления на сферической границе можно найти матрицу оптической системы любой сложности. Порядок перемножения матриц обратный по отношению к порядку, в котором луч встречает элементы оптической схемы.
Оптическая сила тонкой линзы.
Матрица тонкой линзы 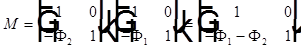 , где
, где 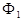 и
и 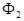 — оптические силы двух границ тонкой линзы. Если ввести обозначение для оптической силы линзы
— оптические силы двух границ тонкой линзы. Если ввести обозначение для оптической силы линзы 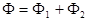 , то матрица тонкой линзы будет выглядеть также как матрица сферической границы
, то матрица тонкой линзы будет выглядеть также как матрица сферической границы 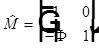 .
.
Для тонкой линзы из материала с показателем преломления 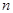 , расположенной в вакууме оптическая сила равна
, расположенной в вакууме оптическая сила равна 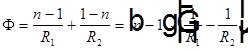 .
.
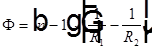 — оптическая сила тонкой линзы, где
— оптическая сила тонкой линзы, где 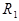 и
и 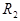 — радиусы кривизны двух поверхностей линзы. Здесь для двояковыпуклой линзы
— радиусы кривизны двух поверхностей линзы. Здесь для двояковыпуклой линзы 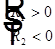 .
.
В параксиальной оптике удобно принять следующее правило знаков для величин с размерностью длины. Пусть ось x направлена вдоль оптической оси. Пусть 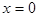 — положение сферической границы или тонкой линзы. Будем считать, что радиус кривизны границы
— положение сферической границы или тонкой линзы. Будем считать, что радиус кривизны границы 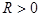 , если центр кривизны имеет x координату
, если центр кривизны имеет x координату 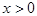 .
.
Формула тонкой линзы. Сопряженные плоскости.
Фокусное расстояние. Фокальная плоскость. Фокус.
Рассмотрим две опорные плоскости на расстояниях 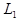 и
и  с двух сторон тонкой линзы с оптической силой
с двух сторон тонкой линзы с оптической силой 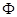 . Матрица перехода от первой ко второй опорной плоскости
. Матрица перехода от первой ко второй опорной плоскости 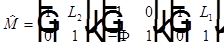 =
= 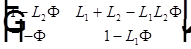 .
.
В соответствии с этой матрицей 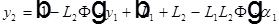 . Рассмотрим это уравнение применительно к точечному предмету в первой опорной плоскости и его изображению во второй опорной плоскости. Плоскости предмета и изображения называются сопряженными плоскостями. Тогда пучок лучей, выходящих из точки
. Рассмотрим это уравнение применительно к точечному предмету в первой опорной плоскости и его изображению во второй опорной плоскости. Плоскости предмета и изображения называются сопряженными плоскостями. Тогда пучок лучей, выходящих из точки 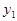 под любыми углами
под любыми углами 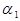 должен собраться в точку
должен собраться в точку 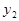 . Если равенство сохраняется при любом
. Если равенство сохраняется при любом 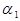 , то коэффициент при
, то коэффициент при 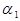 должен быть равен нулю
должен быть равен нулю 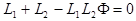 . Откуда
. Откуда 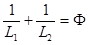 .
.
Если среды слева и справа от тонкой линзы имеют показатели преломления 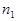 и
и 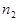 , то во всех формулах этого вывода нужно заменить
, то во всех формулах этого вывода нужно заменить 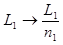 и
и 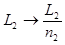 . Тогда
. Тогда 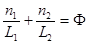 .
.
Учтем теперь правило знаков в параксиальной оптике. Если предмет слева от линзы и его x координата равна 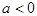 , а изображение справа от линзы и его x координата равна
, а изображение справа от линзы и его x координата равна 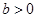 , то
, то
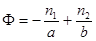 — формула тонкой линзы.
— формула тонкой линзы.
Пусть теперь на линзу падает параллельный пучок лучей (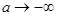 ), тогда точка, в которой он собирается, называется фокусом линзы (задним фокусом). Координата фокуса относительно линзы называется фокусным расстоянием
), тогда точка, в которой он собирается, называется фокусом линзы (задним фокусом). Координата фокуса относительно линзы называется фокусным расстоянием 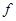 . Тогда
. Тогда
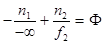 , откуда
, откуда 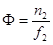 .
.
Если свет выходит из некоторой точки на оптической оси, и после линзы свет идет в виде параллельного пучка лучей, то 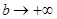 и свет выходит из переднего фокуса, а его координата относительно линзы равна переднему фокусному расстоянию
и свет выходит из переднего фокуса, а его координата относительно линзы равна переднему фокусному расстоянию 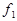 .
.
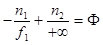 .
.
Оба фокусных расстояния связаны с оптической силой линзы соотношением
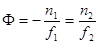 .
.
Фокальная плоскость — плоскость перпендикулярная оптической оси и проходящая через фокус.
Построение изображений в тонкой линзе. Действительное и мнимое изображение.
Для построения изображения точечного источника в тонкой линзе достаточно найти пересечение двух любых лучей, выходящих из точечного источника. Есть три удобных луча. Луч, который до линзы идет параллельно оптической оси, после линзы обязан пройти через ее задний фокус. Луч, который до линзы проходит через передний фокус, после линзы пойдет параллельно оптической оси. Луч, который проходит через центр тонкой линзы, пойдет за линзой без изменения направления, если показатель преломления среды до и после линзы один и тот же.
Изображение действительное, если оно расположено за линзой. Изображение мнимое, если лучи за линзой не пересекаются, а пересекаются лишь их продолжения в область перед линзой.
Построение хода произвольного луча при прохождении тонкой линзы.
Возьмите произвольный луч. Пусть этот луч падает на тонкую линзу в точке A. Рассмотрите луч, параллельный заданному лучу и проходящий через передний фокус линзы. Этот второй луч после линзы пойдет параллельно оптической оси и пересечет заднюю фокальную плоскость в некоторой точке B. Заданный луч после линзы проходит через точки A и B.
Сферическое зеркало.
Рассмотрим вогнутое сферическое зеркало. Рассмотрим луч, падающий на зеркало параллельно оптической оси. Из геометрических соображений точка, в которой отраженный луч пересечет оптическую ось, расположена на расстоянии 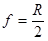 от зеркала, где
от зеркала, где 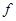 — фокусное расстояние сферического зеркала,
— фокусное расстояние сферического зеркала, 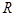 — радиус кривизны зеркала. Для вогнутого зеркала по правилу знаков обе величины положительны.
— радиус кривизны зеркала. Для вогнутого зеркала по правилу знаков обе величины положительны.
Толстая линза. Матрица толстой линзы. Главные плоскости.
Матрица толстой линзы:
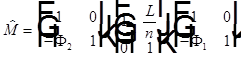 =
= 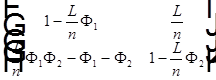 ,
,
где 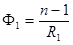 ,
, 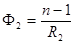 — оптические силы двух сферических поверхностей,
— оптические силы двух сферических поверхностей, 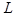 — толщина линзы,
— толщина линзы, 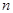 — показатель преломления линзы.
— показатель преломления линзы.
Главные плоскости оптической системы — сопряженные плоскости с единичным коэффициентом усиления.
Гомоцентрический пучок лучей. Приведенный радиус кривизны. Правило ABCD.
В изотропной среде лучи перпендикулярны поверхности равных фаз. Сферический фронт волны соответствует гомоцентрическому пучку лучей. 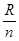 — приведенный радиус гомоцентрического пучка лучей, где
— приведенный радиус гомоцентрического пучка лучей, где 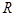 — радиус соответствующего сферического фронта волны.
— радиус соответствующего сферического фронта волны.
Для любой точки гомоцентрического пука лучей выполняется соотношение 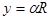 , где
, где 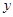 — расстояние от точки на фронте волны до оптической оси,
— расстояние от точки на фронте волны до оптической оси, 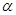 — угол между лучом, проходящем через рассматриваемую точку, и оптической осью. Тогда
— угол между лучом, проходящем через рассматриваемую точку, и оптической осью. Тогда 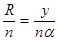 — приведенный радиус равен отношению координат луча.
— приведенный радиус равен отношению координат луча.
Пусть гомоцентрический пучок лучей проходит через оптическую систему с матрицей 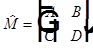 . Тогда
. Тогда 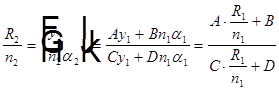 . Откуда
. Откуда
 — правило ABCD, или правило преобразования приведенного радиуса гомоцентрического пучка лучей.
— правило ABCD, или правило преобразования приведенного радиуса гомоцентрического пучка лучей.
Факультативно. Гауссовы пучки.
Хорошим приближением для лазерного пучка лучей является гауссов пучок. Пусть световая волна распространяется вдоль оси z. Будем называть пучок лучей гауссовым, если поле 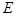 световой волны можно найти по формуле
световой волны можно найти по формуле
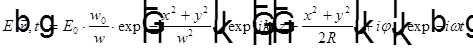 ,
,
где 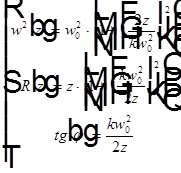 .
.
Здесь 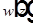 — зависимость радиуса пучка от координаты вдоль оси пучка,
— зависимость радиуса пучка от координаты вдоль оси пучка, 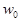 — радиус шейки каустики, шейка каустики — самое узкое место каустической поверхности
— радиус шейки каустики, шейка каустики — самое узкое место каустической поверхности 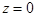 , каустическая поверхность — поверхность, огибающая все лучи.
, каустическая поверхность — поверхность, огибающая все лучи. 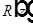 — зависимость радиуса кривизны гомоцентрического пучка лучей от координаты вдоль оси пучка.
— зависимость радиуса кривизны гомоцентрического пучка лучей от координаты вдоль оси пучка. 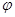 — фазовый сдвиг относительно фазы плоской волны вдоль оси z.
— фазовый сдвиг относительно фазы плоской волны вдоль оси z.
Шейка каустики не отображается линзой по законам геометрической оптики. Преобразование гауссова пучка лучей тонкой линзой определяется изменением приведенного радиуса кривизны по правилу ABCD. Если рассмотреть две опорные плоскости непосредственно перед тонкой линзой и сразу после линзы, то 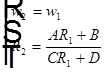 . По первым двум уравнениям приведенной выше системы из трех уравнений по известным значениям
. По первым двум уравнениям приведенной выше системы из трех уравнений по известным значениям 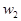 и
и 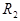 можно найти
можно найти 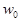 и
и 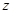 новой каустической поверхности.
новой каустической поверхности.
Глаз.
Свет и цвет.
Лупа. Увеличение лупы.
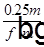
Окуляр.
Подзорная труба или телескоп. Труба Кеплера. Труба Галилея.
Угловое увеличение телескопа.
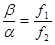
Микроскоп.
Призменный спектрометр. Выбор положения элементов схемы: источника света,
конденсорной линзы, коллиматорной линзы, призмы, репера и окуляра.
Аберрация (искажение). Хроматическая аберрация, сферическая аберрация,
астигматизм, дисторсия, кома.
Факультативно. Апертурная диафрагма. Входной и выходной зрачки.
Апертура. Относительное отверстие.
Распространение света в неоднородной среде. Эйконал. Уравнение эйконала.
l — геометрическая длина пути.
L — оптическая длина пути.
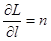
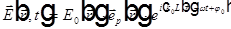
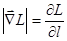
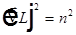
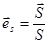
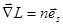
Уравнение для вычисления траектории луча в неоднородной среде.
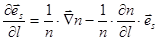
Распространение света в среде, в которой показатель преломления n зависит только от вертикальной координаты z.
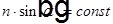
Принцип Ферма.
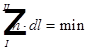
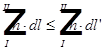
Миражи. Рефракция.
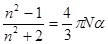 , где N — концентрация молекул, α — поляризуемость молекулы.
, где N — концентрация молекул, α — поляризуемость молекулы.
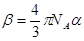 — рефракция или молекулярная рефракция, NA — число Авогадро.
— рефракция или молекулярная рефракция, NA — число Авогадро.
Тема 7. Спектр света.
Разложение света по положительным частотам.
Прямое преобразование Фурье:
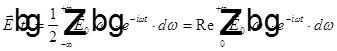 .
.
Обратное преобразование Фурье:
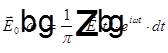 .
.
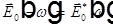
Ряд Фурье:

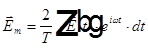 ,
, 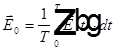
Спектр света. Спектральная плотность интенсивности света и ее связь с интенсивностью.
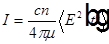
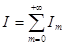
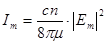 ,
, 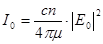 , где
, где
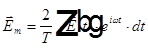 ,
, 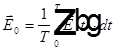
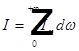
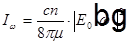
Спектр огибающей светового импульса и спектр самого импульса.
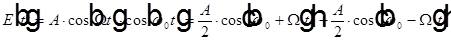
Преобразование Фурье гауссовой функции времени.
Соотношение неопределенности времени и частоты.
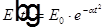 ,
, 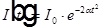 ,
,
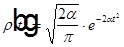 ,
, 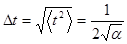 ,
,
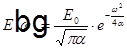 ,
, 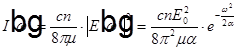 ,
,
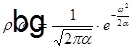 ,
, 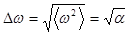 ,
,
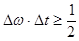
Факультативно. Разложение света по плоским монохроматическим волнам.
 , где
, где 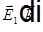 из
из
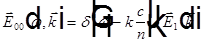 , где
, где 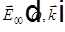 из
из
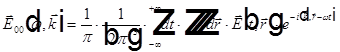
Тема 8. Интерференци я.
Явление интерференции. Ширина полос. Видность.
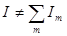 — интерференция.
— интерференция.
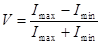 — видность интерференционной картины.
— видность интерференционной картины.
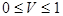
Интенсивность света при сложении двух световых волн ортогональных поляризаций.
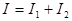
Интенсивность света при сложении двух световых волн одинаковой поляризации как функция разности фаз.
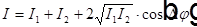
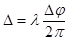 ,
, 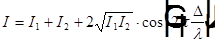
Связь ширины интерференционных полос и угла между интерферирующими волнами.
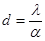
Метод деления амплитуды.
Интерференция волн отраженной и прошедшей полупрозрачную пластинку.
Интерференция света при отражении от плоскопараллельной пластины.
Интерферометр Майкельсона.
Метод деления волнового фронта.
Опыт Юнга.
Бипризма Френеля.
Зеркало Ллойда.
Билинза Бийе.
Порядок интерференции. Номер интерференционной полосы.
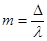 , где m — номер полосы, Δ — оптическая разность хода.
, где m — номер полосы, Δ — оптическая разность хода.
Когерентность. Частично когерентный свет.
Квазимонохроматический свет. Спектральная ширина источника света.
Время когерентности. Длина когерентности.
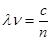 =>
=> 
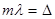 =>
=> 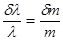
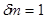 =>
=> 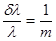 =>
=> 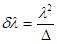
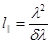 — длина когерентности,
— длина когерентности,
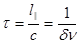 — время когерентности.
— время когерентности.
Пространственная когерентность.
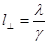 , где
, где 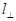 — длина пространственной когерентности,
— длина пространственной когерентности, 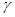 — угловой размер источника света.
— угловой размер источника света.
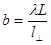 , где b — линейный размер источника света, L — расстояние от точки наблюдения до источника света,
, где b — линейный размер источника света, L — расстояние от точки наблюдения до источника света,
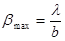 , где
, где 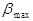 — максимально допустимая апертура интерференции.
— максимально допустимая апертура интерференции.
Объем когерентности.
Звездный интерферометр Майкельсона. Измерение угловых размеров звезд.
Понятие об эффекте группировки фотонов. Параметр вырождения света.
Оптический аналог опыта Брауна-Твисса.
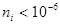 — для нелазерных источников света,
— для нелазерных источников света,
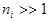 — для лазерных источников света.
— для лазерных источников света.
Локализация интерференционной картины
на примере наблюдения интерференции в схеме с бипризмой Френеля.
Полосы равного наклона.
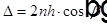 , где
, где 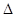 — оптическая разность хода,
— оптическая разность хода, 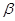 — угол преломления плоскопараллельной пластинки толщиной h.
— угол преломления плоскопараллельной пластинки толщиной h.
Полосы равной толщины.
Кольца Ньютона.
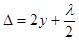
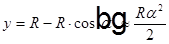 , где R — радиус кривизны сферической поверхности, α — угол между вертикалью и направлением из центра кривизны на точку наблюдения интерференционной картины
, где R — радиус кривизны сферической поверхности, α — угол между вертикалью и направлением из центра кривизны на точку наблюдения интерференционной картины
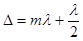 — разность хода для темной полосы с номером m =>
— разность хода для темной полосы с номером m => 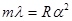
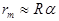 — радиус m-ого темного кольца =>
— радиус m-ого темного кольца => 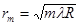
Полосы равного наклона и равной толщины в интерферометре Майкельсона.
Интерферометр Жамена.
Интерферометр Рождественского (Маха-Цендера).
Тема 9. Дифракция.
Интегральная теорема Кирхгофа.
Пусть 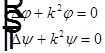 , тогда
, тогда 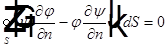
Если 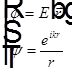 , то
, то 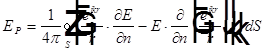 , где EP — комплексная амплитуда поля в точке наблюдения P, S — замкнутая поверхность вокруг точки наблюдения, r — расстояние от точки наблюдения до элемента поверхности dS, n — внешняя нормаль поверхности.
, где EP — комплексная амплитуда поля в точке наблюдения P, S — замкнутая поверхность вокруг точки наблюдения, r — расстояние от точки наблюдения до элемента поверхности dS, n — внешняя нормаль поверхности.
Скалярная теория дифракции Кирхгофа.
Пусть источник света точечный 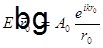 , тогда
, тогда
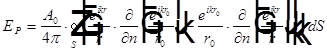 =>
=>
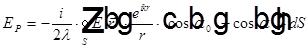 , где
, где
EP — комплексная амплитуда света в точке наблюдения (r=0),
α0 — угол между направлением света, пришедшего от источника к элементу поверхности dS, и внутренней нормалью к поверхности S,
α — угол между направлением внутренней нормали и направлением от элемента поверхности dS на точку наблюдения P.
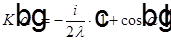 — коэффициент наклона.
— коэффициент наклона.
Дифракция Френеля.
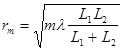 — радиус m-ой зоны Френеля, где L1 — расстояние от источника до отверстия, L2 — расстояние от отверстия до точки наблюдения.
— радиус m-ой зоны Френеля, где L1 — расстояние от источника до отверстия, L2 — расстояние от отверстия до точки наблюдения.
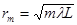 — радиус m-ой зоны Френеля для плоской волны до отверстия.
— радиус m-ой зоны Френеля для плоской волны до отверстия.
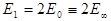 =>
=> 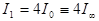
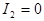
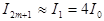
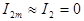
Пятно Пуассона.
Зонная пластинка. Фокус зонной пластинки. Отношение интенсивностей в фокусе линзы и зонной пластинки. Ложные фокусы зонной пластинки.
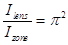
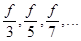
Дифракция Фраунгофера на круглом отверстии.
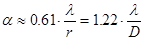 — угловой радиус первого темного кольца
— угловой радиус первого темного кольца
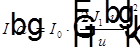 , где
, где 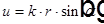 ,
, 
Дифракция Фраунгофера на одной щели.
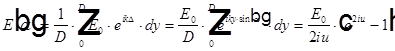 , где
, где 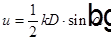
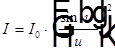
Дифракция Фраунгофера на прямоугольном отверстии.
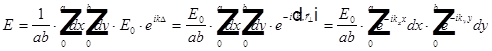
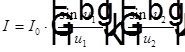 , где
, где 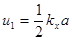 ,
, 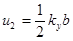
Принцип Бабине.
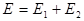
Факультативно. Дифракция Фраунгофера и
Фурье-образ амплитудного коэффициента пропускания.
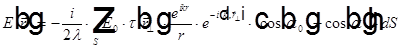
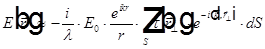
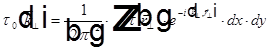
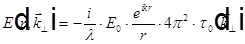
Дифракция Френеля на краю экрана. Спираль Корню.
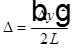
Тема 10. Дифракционная решетка.
Главные дифракционные максимумы решетки.
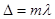 , где
, где 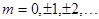 — порядок дифракции
— порядок дифракции
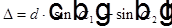 , где d — шаг решетки, α1 — угол падения света, α2 — угол дифракции.
, где d — шаг решетки, α1 — угол падения света, α2 — угол дифракции.
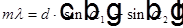 — уравнение для угла дифракции
— уравнение для угла дифракции 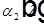 m-ого порядка дифракции.
m-ого порядка дифракции.
Угловая ширина дифракционного максимума решетки.
 , где N — число штрихов решетки, d — шаг решетки, D — ширина решетки.
, где N — число штрихов решетки, d — шаг решетки, D — ширина решетки.
Date: 2015-05-09; view: 579; Нарушение авторских прав