Поглощение света 1 page

Когда гармоническая электромагнитная волна частоты ω проходит че­рез вещество, она принуждает электроны в молекулах совершать колеба­ния с такой же частотой. При этом волна постепенно теряет свою энер­гию, передавая ее колеблющимся электронам. Колеблющиеся электро­ны испускают электромагнитные волны, которые уносят с собой часть их энергии. Некоторая часть энергии колебаний электронов в молекулах переходит в энергию беспорядочного теплового движения самих моле­кул. Вследствие этих процессов интенсивность электромагнитной волны уменьшается по мере ее продвижения через вещество. Это явление на­зывают поглощением излучения веществом.

Пусть плоская электромагнитная волна распространяется в веществе. Направим ось х вдоль одного из лучей в сторону распространения волны. Если вещество поглощает энергию волны, то ее интенсивность I будут монотонно убывающей функцией координаты х:

I=I(x)

Приращение dI этой функции, соответствующее приращению dx коорди­наты, будет отрицательной величиной: dI < 0. При этом абсолютное значение | dI | приращения интенсивности должно быть прямо пропорци­онально длине интервала dx и самой интенсивности. Таким образом, приращение интенсивности волны будет

dI = - a I dx, (15.25)

где коэффициент пропорциональности а называется коэффициентом по­глощения. Эта величина является характеристикой вещества.

Равенство (15.25) есть дифференциальное уравнение с разделяющими­ся переменными, которое следует записать так:

dI/ I = - a dx,

Интегрирование приводит к функции

I(x) =C e^{- ax}

где С - постоянная интегрирования. Пусть значение координаты х = 0 соответствует фазовой плоскости, на которой интенсивность волны при­нимает значение I₀

I(0) = I ₀. (15.26)

При помощи этого граничного условия нетрудно установить, что посто­янная

С = I₀. Таким образом, получим зависимость

I(х) = I₀е^-ах, (15.27)

которая выражает закон Вугера. Если коэффициент поглощения а равен нулю, то интенсивность волны будет постоянной величиной: I= I₀. Это означает, что излучение проходит через вещество без поглощения. Такие вещества называют прозрачными для излучения. Чем больше значение коэффициента поглощения а в формуле (15.27), тем быстрее убывает интенсивность волны при ее распространении через вещество.

Коэффициент поглощения а определяется свойствами вещества и явля­ется некоторой функцией частоты ω проходящего через вещество излу­чения: а = а(ω). Вынужденные колебания электронов под действием гармонической волны происходят с наибольшей амплитудой в том слу­чае, когда частота волны ω близка к одной из частот ω_0i собственных колебаний электронов. При этом электроны забирают у волны больше всего энергии. Когда частота волны ω далека от частот ω_0i, амплиту­да вынужденных колебаний электронов очень мала, т.е. такая волна не может заставить электроны колебаться со своей частотой и не передает им свою энергию. Волны с такими частотами проходят через вещество без потерь энергии, т.е. вещество их не поглощает и является для них прозрачным (а = 0).

Интервалы частот, в которых коэффициент поглощения заметно от­личается от нуля, называют полосами поглощения. Частоты ω_0i соб­ственных колебаний электронов лежат в этих интервалах. Полосы по­глощения электромагнитных волн газами очень узкие. Поэтому спек­тры поглощения излучения газами называют линейчатыми. Спектры поглощения излучения твердыми телами, жидкостями и газами при вы­соких давлениях содержат широкие полосы поглощения. Расширение полос поглощения при увеличении плотности вещества происходит из-за уменьшения среднего расстояния между атомами, что приводит к более интенсивному их взаимодействию.

Проводники практически непрозрачны для электромагнитного излу­чения, так как они содержат в себе носители тока. Когда электромаг­нитная волна проникает на некоторую глубину в проводник, она заста­вляет носители тока двигаться, т.е. волна возбуждает в проводнике пе­ременные электрические токи. Это приводит к нагреванию проводника. Таким образом, энергия волны посредством носителей тока переходит в тепловую энергию. Вследствие этого интенсивность волны очень быстро уменьшается при ее продвижении в глубь проводника.

Краткое математическое содержание волоновой оптики

1. Световые волны в прозрачной изотропной среде.

Волновые уравнения для светового поля.

Уравнения Максвелла 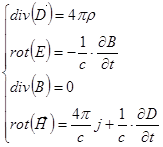рассмотрим при условиях: 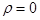, , 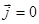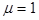. Из ротора второго уравнения с учетом четвертого получим 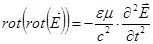. С другой стороны для любого векторного поля 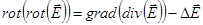. Откуда получаем волновое уравнение для поля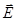

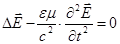
где 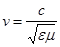— скорость волны. 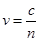— определение показателя преломления 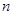. Следовательно .

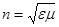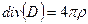
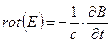
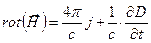
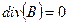
Факультативно. Частные решения волнового уравнения.

Разделение временной и пространственных переменных решения волнового уравнения .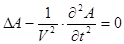

Пусть 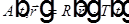, подставим в волновое уравнение для A и разделим уравнение на RT, тогда одно слагаемое зависит только от 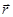, а другое — только от t. Следовательно, каждое из двух слагаемых равно константе, которую обозначим за 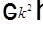. Тогда для функции координат получим 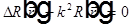— уравнение Гельмгольца, а для функции времени 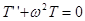— уравнение гармонических колебаний, где .

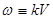Разделение переменных решения уравнения Гельмгольца в декартовых координатах, пусть 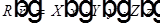. Подставим это решение в уравнение Гельмгольца и разделим его на произведение XYZ. При этом слагаемые уравнения окажутся функциями разных переменных и, следовательно, каждое слагаемое — константа: 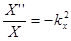, , 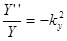, 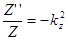где 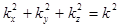. Решения для X, Y, Z — гармонические колебания от x, y, z.

Подставляя решения для X, Y, Z в R, а затем решения для R и T в A, получаем — решение в комплексной форме в виде плоских волн .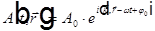

Разделение переменных в других системах координат приводит к другим решениям. Среди множества решений в цилиндрической системе координат отметим решение в виде цилиндрической волны 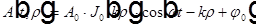, где 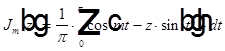— функция Бесселя с целым значком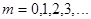

Среди множества решений в сферической системе координат отметим решение в виде сферической волны .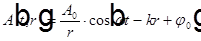

Параметры плоской волны.

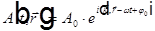
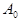— амплитуда волны,

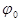— начальная фаза волны,

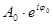— комплексная амплитуда волны,

T — период, 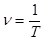— частота, 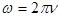— циклическая частота волны,

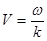— фазовая скорость волны,

λ — длина волны, k — волновое число, 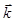— волновой вектор,

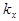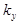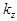, , — циклические пространственные частоты волны,

— фаза волны.

Фазовая скорость.

Рассмотрим плоскую волну, и направим ось z вдоль вектора 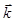. Тогда 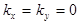, => 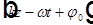— фаза волны. Тогда 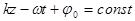— уравнение постоянной фазы. Поскольку в это уравнение входит в качестве параметра время t, то это уравнение — уравнение движения поверхности постоянной фазы, движения фазовой поверхности.

Продифференцируем это уравнение по времени и получим 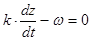откуда 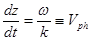, где

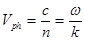— фазовая скорость волны.

Групповая скорость.

Рассмотрим две волны некоторой физической переменной A с разными, но близкими частотами, бегущие вдоль оси z 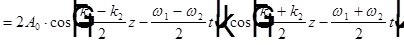. Введем обозначения 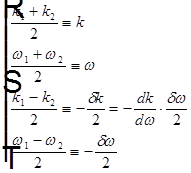, тогда 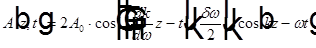, где 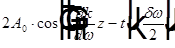можно рассматривать, как медленно меняющуюся амплитуду суммарной волны.

Для огибающей (или амплитуды) волны уравнение постоянной фазы примет следующий вид 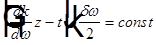. Дифференцируя это уравнение по времени, получаем 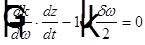и, следовательно, .

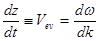Окончательно, 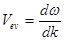— групповая скорость волны, сравните с фазовой скоростью волны .

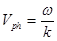Поперечность световых волн.

Рассмотрим выражение для плоской волны любой природы 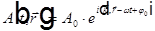. Продифференцируем его по времени и получим 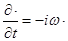. Аналогично, дифференцируя по пространственным координатам, получим 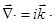. Подставим эти выражения в уравнения Максвелла. Начнем с первого уравнения 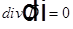=> => 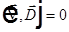=> => 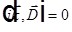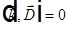, но 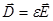, тогда .

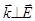Аналогично получаем: 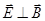, , 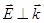, , 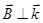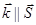где 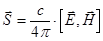— вектор Пойнтинга.

Соотношение длин векторов E и H в бегущей световой волне.

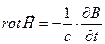
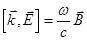=> , но 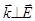, тогда 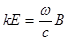=> 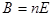,откуда 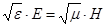в системе СГС Гаусса, или 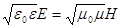в системе СИ.

Интенсивность света.

Интенсивность 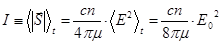— плотность потока энергии (энергия в единицу времени через единицу площади).

Связь интенсивности света с объемной плотностью энергии световой волны.

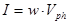, где 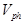— фазовая скорость света, хотя казалось бы, должна быть групповая.

Тема 2. Поляризация света.

Линейная поляризация.

Если световая волна бежит вдоль оси z, то вектор колеблется в плоскости x,y. В каждый момент времени вектор можно представить, как сумму двух векторов, один из которых направлен вдоль оси X, а другой — вдоль оси Y. Соответственно говорят, что бегущую световую волну всегда можно разложить на две линейно поляризованные волны.

Плоскость поляризации света — плоскость векторов 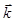и .

Единичный вектор линейной поляризации — единичный вектор вдоль .

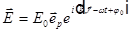
Пленочный поляризатор (поляроид).

Поляроид изготавливают из целлулоидной пленки с вкраплениями вещества с оптическим дихроизмом (вытянутые молекулы). Дихроизм — различное поглощение света различных поляризаций. Двулучепреломление — различные показатели преломления для света различных поляризаций.

Поляризационные очки для стереокино.

Разница изображений, полученных двумя разнесенными кинокамерами.

Стереоэффект возникает, когда каждый глаз видит изображение, полученное соответствующей кинокамерой.

Циркулярно поляризованный свет или свет круговой поляризации.

Если ,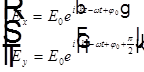

то

.

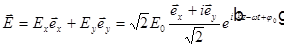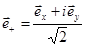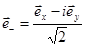и — единичные векторы левой и правой циркулярно поляризованных волн, 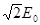— амплитуда циркулярно поляризованной волны, где 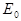— амплитуда каждой их двух линейно поляризованных волн.

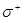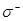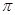, , - компоненты света.

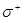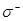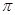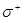Разложение колебаний поля или диполя на , , компоненты зависит от выбора направления оси квантования и не зависит от направления света. Колебания вдоль оси квантования — компонента света. Вращения в плоскости перпендикулярной оси квантования — и 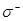компоненты света.

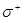компоненте в эффекте Зеемана соответствует свет с большей частотой (исторически, наоборот, с большей длиной волны).

Если свет распространяется вдоль оси квантования, то 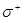компоненте света соответствует единичный вектор поляризации 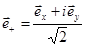и левая циркулярно поляризованная волна, в которой вектор поля волны вращается влево в каждой точке пространства, если смотреть навстречу волне. Если волна распространяется вдоль оси z, то в левой циркулярно поляризованной волне 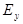компонента света отстает по фазе на 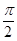от 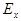компоненты.

К экзамену знать не нужно, но 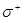компоненте соответствует линия поглощения света с изменением квантового числа проекции магнитного момента на ось квантования , на верхнем уровне энергии квантовое число на единицу больше, чем на нижнем уровне.

Эллиптическая поляризация света.

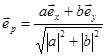— единичный вектор эллиптической поляризации.

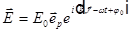— поле световой волны эллиптически поляризованного света.

Естественный или неполяризованный свет — свет, в котором разность фаз между двумя ортогональными линейными поляризациями случайна, или, что то же самое — это эллиптически поляризованный свет, в котором параметры эллипса случайным образом изменяются.

Тема 3. Излучение и поглощение света.

Излучение и поглощение света.

Электромагнитные волны излучают только ускоренно движущиеся заряды.

Свет излучают атомы. Линейный размер атома примерно в 1000 раз меньше длины волны видимого света. Если размер излучателя гораздо меньше длины волны излучения, то чем выше осциллирующий мультипольный момент системы зарядов, тем слабее его излучение. Поэтому в оптике обычно считают, что излучает только электрический дипольный момент атома — излучение в дипольном приближении.

Поле точечного диполя на расстоянии гораздо большем длины волны (в волновой зоне) находится выражением: .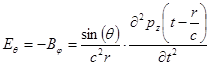

Основные свойства излучения диполя:

1. Направление излучения — от диполя , .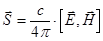

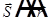2. в любой момент времени в любой точке пространства.

3. 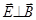в любой момент времени в любой точке пространства.

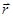4. лежит в плоскости и .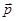

5. .

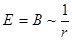6. Диаграмма направленности излучения диполя , .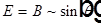

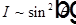Поглощение диполем света плоской волны происходит в том случае, если при сложении излученной диполем волны с проходящей мимо волной получается волна с меньшей амплитудой.

Тема 4. Отражение и преломление света.

Отражение света и стоячие волны.

Узлы и пучности стоячей волны.

Потеря полуволны при отражении света от зеркала.

Продольные и поперечные моды лазера.

Индекс моды — число узлов стоячей волны.

Индекс продольной моды. Индексы поперечных мод. Изменение частот продольных мод при изменении длины резонатора лазера.

Пленка Троицкого.

Селекция продольных мод лазера осуществляется установкой пленки Троицкого в узел продольной моды.

Закон Снеллиуса (закон преломления) и закон отражения света.

Пусть граница двух сред находится в плоскости x,y, а свет падает на границу в плоскости x,z.

Три световые волны обозначим индексами: i (input) — падающая волна, r (reflect) — отраженная, t (transpierce — пронзать насквозь) — прошедшая волна. Введем обозначения: 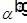— угол падения (между нормалью к границе и лучом), 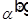— угол отражения, 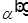— угол преломления.

Граничные условия для электрического и магнитного полей должны выполняться в каждой точке границы двух сред. Для этого необходимо, чтобы все три волны имели на границе одинаковую пространственную частоту. Тогда .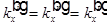

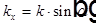для каждой из трех волн. Откуда получаем .

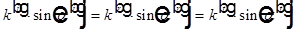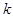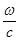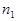Подставим в равенство вместо величины его значение , сократим равенство на и получим , где и 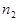— показатели преломления двух сред. С учетом того, что 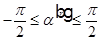, получим

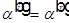— угол падения равен углу отражения или закон отражения.

Обозначим 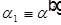и и 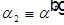получим закон преломления или закон Снеллиуса:

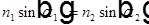
Формулы Френеля для амплитудных коэффициентов отражения и пропускания света.

Амплитуды отраженной и преломленной волн можно найти из граничных условий для полей E и B: .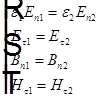

Часть граничных условий удобно заменить учетом ортогональности световых волн и учетом закона отражения и закона преломления.

Далее удобно рассмотреть раздельно вариант поляризации света в плоскости падения и вариант поляризации перпендикулярной плоскости падения.

Для поляризации в плоскости падения рассмотрим первое уравнение системы, в котором нормальная составляющая поля находится умножением на синус угла между лучом и нормалью к границе:

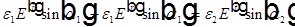
Разделим это уравнение на 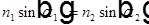и получим 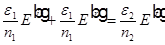. Что с учетом 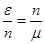перепишем в виде .

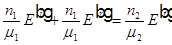Для нахождения амплитуд отраженной 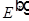и преломленной 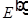волн нужно еще одно уравнение. Рассмотрим второе уравнение системы, где проекция поля на горизонтальное направление получается умножением напряженности поля на косинус угла:

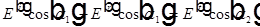
Решая два уравнения с двумя неизвестными, находим

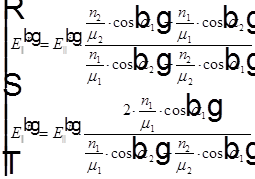
Обычно в этих выражениях пренебрегают отличием магнитной проницаемости среды от единицы (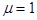). Окончательно для амплитудных коэффициентов отражения 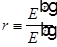и пропускания 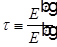получаем следующие выражения

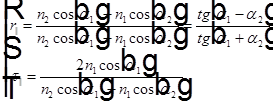— это формулы Френеля для поляризации света в плоскости падения.

Для поляризации света перпендикулярной плоскости падения из граничных условий с учетом соотношения 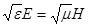получаем пару уравнений для амплитуд отраженной и преломленной волн: .

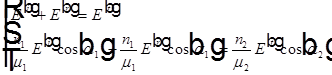Решая уравнения, находим 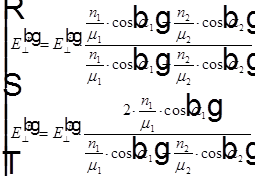и, заменяя 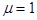, получаем

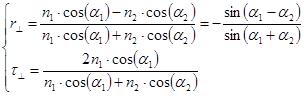— формулы Френеля для поляризации света перпендикулярной плоскости падения.

Угол Брюстера и брюстеровские окна лазерных трубок.

=> =>

=> =>

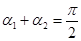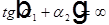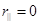
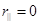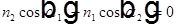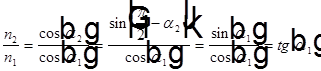
Date: 2015-05-09; view: 695; Нарушение авторских прав