
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интерференция света от двух точечных источников
|
|
Рассмотрим интерференцию гармонических волн, испускаемых двумя точечными источниками. Уравнение гармонической световой волны, распространяющейся от точечного источника в однородной изотропной среде, имеет вид
E(t, r) = A(r) cos(ωt- kr + a),
где E(t, r) - одна из составляющих вектора напряженности электрического поля; r - расстояние от источника до рассматриваемой точки Р пространства; А(r) - амплитуда волны в данной точке.
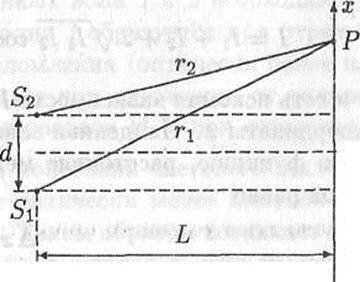
Рис. 12.2.Интерференция света от двух точечных источников
Пусть две гармонические волны с одинаковыми частотами и коллинеарными векторами Е 1 и Е 2 от источников S1 и S2 приходят в некоторую точку пространства Р (рис. 12.2). Эти волны создают в точке Р гармонические колебания
Е1 =A1 cos(ωt- kr1 + a1), E2 = A2 cos(ωt - kr2 + a2), (12.22)
где r1 и r2 - расстояние от источников света до точки Р. Разность фаз этих колебаний будет
φ2-φ1 = (2π/λ) (r1 - r2) + a2- a1 (12.23)
.
Пусть на расстоянии L от источников света расположен экран, на котором наблюдается интерференционная картина (рис. 12.2). Найдем распределение интенсивности света на оси х, параллельной отрезку, который соединяет источники Si и S2. Обозначим длину этого отрезка d. Начало отсчета координаты х поместим в точку О, равноудаленную от обоих источников. Из прямоугольных треугольников на рис. 12.2 найдем, что
r12=L2 + (x+d/2)2 r22=L2 + (x-d/2)2
При этом
r12 - r22 = 2xd
(12.24)
Обычно в интерференционных опытах d << L и x << L. В таких случаях r1 ~ r2 ~ L и равенство (12.24) приводит к формуле
r1 - r2 = xd/L (12.25)
Используя формулы (12.23) и (12.25), выражению (12.7) можно придать вид
I=I1 + I2 +2√ I1I2cos(2πxd/(λL)+a2 –a1)) (12.26)
Это и есть искомая зависимость I = I(x) интенсивности света на экране от координаты х. Найденная зависимость представляет собой периодическую функцию, расстояние между максимумами (или минимумами) которой равно
∆x = λL/d (12.27)
Величина ∆x называется шириной интерференционной полосы.
Интересно отметить, что впервые длины волн для различных участков видимой области спектра были вычислены по формуле (12.27) после того, как в опытах по интерференции света были измерены расстояния ∆x между полосами.
Date: 2015-05-09; view: 1146; Нарушение авторских прав