
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Плоская гармоническая электромагнитная волна
|
|
Рассмотрим плоскую гармоническую электромагнитную волну, которая описывается функциями (11.24), (11.25), (11.28), (11.29) и (11.31).
Согласно этим формулам векторы Е и H имеют следующие проекции на координатные оси:
Ex=0, Eу = 0, Ez(t,y)=Emcos(ωt-ky+a)
Hx(t,y) = Hmcos(ωt-ky + a), Ну=0, Hz = 0. (11.33)
Эти функции описывают распространяющуюся вдоль оси у плоскую гармоническую электромагнитную волну, в которой вектор Е всегда направлен вдоль оси z, а вектор H - вдоль оси х (рис. 11.4). Такая волна называется плоско, или линейно поляризованной. На рис. 11.4 показан один из лучей. Фазовые плоскости в данном случае параллельны
плоскости ху. На фазовой плоскости векторы Е и H всюду одинаковы. Они изменяются только вдоль луча. Как видно в этом примере,
векторы Е, Н и волновой вектор к в любой точке пространства взаимно перпендикулярны и образуют правую тройку. Это общее свойство электромагнитных волн. Как уже говорилось, электромагнитные волны являются поперечными, т.е. векторы Е и H ортогональны к лучу, вдоль которого распространяется волна. Соотношение (11.30), связывающее модули этих векторов, также выполняется для электромагнитных волн любой формы.
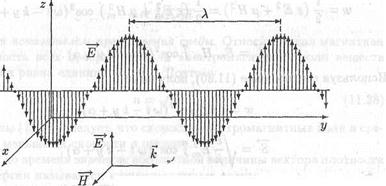
Puc. 114- Плоская гармоническая электромагнитная волна
Запишем функции, определяющие зависимость от времени и координат компонент вектора Е напряженности электрического поля для плоской гармонической электромагнитной волны, распространяющейся вдоль оси х в сторону убывания координаты х. Эти функции имеют вид
Ex=0
Ey(t, x) = Em1 cos(ωt + к у + а)
Ez(t, x) = Em2 cos(ωt + к у + а)
Первое равенство означает, что электромагнитная волна является поперечной. Как видно, в данном случае проекции вектора Е на оси у и z не всегда равны нулю. В этом случае направление вектора напряженности электрического поля может изменяться вдоль луча и с течением времени. Нетрудно показать, что в любой точке пространства конец вектора
Е будет с течением времени описывать эллипс. Поэтому такая волна называется эллиптически поляризованной.
Date: 2015-05-09; view: 1132; Нарушение авторских прав