
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интенсивность волны
|
|
Рассмотрим распространяющуюся вдоль оси у плоскую гармоническую электромагнитную волну, которая описывается функциями (11.32) и (11.33). По формулам (10.11) и (10.12) найдем плотность энергии электромагнитного поля и вектор Умова - Пойнтинга:
S = EmHmj cos2(wt-k y - a). (11.34)
Используя соотношение (11.30), получаем:
w = ε Е2m cos2(w t- к у + a),
где j - единичный вектор, направленный вдоль оси у.
Отметим, что в силу соотношения (11.30) плотности энергии электрического и магнитного полей равны друг другу. Направление вектора 5 плотности потока энергии, как видно из формулы (11.35), совпадает с направлением волнового вектора к, т.е. направление, в котором распространяется энергия электромагнитного поля, совпадает с направлением распространения волны. Плотность энергии w и вектор S зависят от времени и координат. Амплитуды колебаний этих величин
wm = ε Е2m, Sm= (1/2) √ε/μ Е2m
связаны друг с другом простым соотношением
Sm = v wm.
Формулу (11.27), которая определяет скорость v распространения электромагнитной волны, можно записать так:
v=1/ 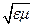 =1/
=1/ 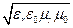
v=c/n
Здесь εr и μr - относительные диэлектрическая и магнитная проницаемости среды, в которой движется электромагнитная волна,
c=1/ 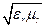
- скорость электромагнитных волн в пустоте, а величина
п = 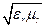 .
.
называется показателем преломления среды. Относительная магнитная проницаемость всех прозрачных для электромагнитных волн веществ практически равна единице: μr ~ 1. Поэтому
n=√εr (11.38)
Из формулы (11.37) следует, что скорость электромагнитных волн в среде в п раз меньше их скорости в пустоте.
Среднее по времени значение абсолютной величины вектора плотности потока энергии называется интенсивностью волны:
I= 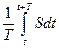
где Т - период волны. Согласно этому определению, размерность и физический смысл интенсивности те же, что и величины S. Подставим в формулу (11.39) выражение (11.35) для модуля вектора Умова - Пойнтинга. После интегрирования получим
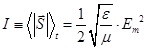
Date: 2015-05-09; view: 699; Нарушение авторских прав