
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритм оптимального назначения
|
|
Есть m работников и m работ.
Каждый из работников выполняет каждую работу с определенной эффективностью.
Требуется распределить работы таким образом, чтобы каждый работник выполнял только одну работу, выполнялись все работы и суммарная эффективность была максимальна среди всех возможных таких распределений.
A = (aij) – матрица эффективности.
А(М*М)
А = 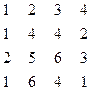
В терминах матрицы эффективности задача состоит в нахождении М элементов, расположенных в разных строках и разных столбцах, чтобы их сумма была максимальной.
Дан двудольный полный граф с V = M, W = M
Даны длины ребер.
Задача состоит в нахождении совершенного паросочетания, сумма длин всех ребер которого максимальна.
Алгоритм.
1. Всем вершинам Vi даем метку аi = max по всем элементам нужной строки.
По всем j присваиваем метку 0.
2. Ищем ребра, для которых выполняется условие
Ai + Bj = Aij
Строим граф, в который входит все вершины исходного графа и найденные ребра.
3. В построенном графе ищем максимальное паросочетание. Если найденное паросочетание совершенно, то алгоритм закончен. Если нет, то переходим дальше.
4. Из теоремы Холла существует подмножество S из V, [S] > ф(S).
Ищем это подмножество.
Для каждой вершины Vi из S метку Ai уменьшают на 1, а для wj из ф(s) метку Vj увеличивают на 1.
5. Переходим на начало шага 2 с новыми значениями меток.
Лекция 15: «Потоки в транспортных сетях»
Введем обозначения
V – вершина орграфа
M-(V) – множество ребер, для которых вершина V является концом.
M+(V) – множество ребер, для которых вершина V является началом.
Транспортной сетью называется связный орграф без петель, для которого выполнены следующие условия
1. Существует только одна вершина A, для которой M-(А) – пустое множество. А – исток.
2. Имеется только одна вершина B, для которой M+(B) – пустое множество. В – сток.
3. Каждому ребру графа поставлено в соответствие целое неотрицательное число, называемое пропускной способностью данного ребра.
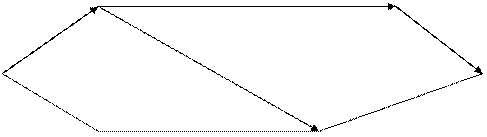 |
2(1) 3(1) 1(1)
6(0)
5(5)

1(1) 4(1) 2(1)

Потоком в транспортной сети (ТС) называется целочисленная функция, определенная на любых ребрах ТС и удовлетворяющая следующим свойствам
1. ф(X) <= C(X), где С(X) – пропускная способность ребра.
На всех ребрах значение функции потока не превосходит значения пропускной способности ребра. Значение функции потока ставим рядом со значением пропускной способности ребра в скобках.
2. Для каждой внутренней вершины V транспортной сети, не равной A или B выполняется следующее условие: суммарная функция потока по ребрам, входящим в вершину, равна суммарной функции потока по ребрам, исходящим из вершины (сколько втекает, столько и вытекает).
Величиной потока [ф] = val(ф) называется число, равное сумме функций потока по всем ребрам, выходящим из вершины А или сумма всех функций потока по всем ребрам, входящим в вершину В.
Выбор потока.
1. Берем путь из А в В.
2. Выбираем минимальную пропускную способность и ставим ее в соответствие каждому ребру из пути.
3. Просматриваем все остальные ребра. Если они не пересекаются, то проделываем для них то же самое, начиная с п1. Всем остальным ребрам ставим в соответствие значение функции потока, равное 0.
Поток в транспортной сети называется максимальным, если выполнено условие
Val(ф) £ Val(Ф*)
Ф* = maximum
Любое подмножество S транспортных вершин, содержащих исток и не содержащих сток, определяет разрез, отделяющий исток от стока (разрез).
Разрез состоит из всех вершит тех ребер, которые имеют свои начала в вершинах множества S, а концы – из дополнения к множеству S.
Пропускной способностью разреза K называется сумма значений пропускных способностей всех ребер этого разреза.
Разрез K** называется минимальным, если для любого другого разреза выполнено условие C(K**) £ C(K).
Теорема Форда – Фалькерсона (без доказательства).
В транспортной сети величина максимального потока равна пропускной способности минимального разреза.
Алгоритм нахождения максимального потока (Алгоритм Форда – Фалькерсона).
1. Берем любой поток в транспортной сети.
2. Строим граф перестроек g* по следующему правилу:
В него входят все вершины исходного графа g.
Те ребра, на которых значение функции потока в исходном графе g были равны 0, входят в новый граф без изменений со своими пропускными способностями.
Все ребра, на которых ф(x) > 0 в новом графе g* заменяются двумя ребрами x* и x**. Ребро x* направлено в ту же сторону, что и x, и пропускная способность c(x*) = c(x) – ф(x).
Ребро x** направлено в противоположную сторону ребру x, и пропускная способность c(x**) = ф(x).
Ребра с нулевой пропускной способностью можно не рисовать.
3. В графе g* ищем путь из А в В по ребрам с ненулевой пропускной способностью. Если его нет, то имеющийся поток является максимальным и алгоритм закончен. Иначе переходим к пункту 4.
(Этот путь называется увеличенной цепью. D = min(c(x)) – минимальное значение пропускной способности этой цепи).
4. Меняем значение функции потока в графе g для тех ребер, которые соответствуют найденному пути в графе перестроек по следующему правилу:
Если направление ребра x в графе g совпадает с направлением пути, то новое ф(x) = ф(x) + D
Если же направление противоположно направлению пути, то ф(x) = ф(x) - D
5. Переходим на шаг 2 с новым потоком.
Лекция 15: «Элементы комбинаторики»
Перестановки. Размещения. Сочетания
Пусть есть некоторое конечное множество элементов U ={ a 1, a 2,..., a n}. Рассмотрим набор элементов 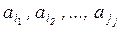 ,
, 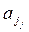 где Î U, j = 1, 2,..., r.
где Î U, j = 1, 2,..., r.
Этот набор называется выборкой объема r из n элементов. Любое подмножество U является выборкой, но не всякая выборка является подмножеством U, так как в выборку один и тот же элемент может входить несколько раз (в отличие от подмножества).
Комбинаторные задачи связаны с подсчетом числа выборок объема r из n элементов, где выборки подчиняются определенным условиям, т.е. выбор производится по какому-нибудь принципу. Подсчет числа выборок основывается на двух правилах теории множеств.
Принцип суммы: если card A = m, card B = n и A Ç B = Æ, то card A È B = = m + n. На комбинаторном языке это означает: если объект A можно выбрать m способами, объект B другими n способами и их одновременный выбор невозможен, то выбор “ A или B ” может быть осуществлен m + n способами.
Принцип произведения: если card A = m, card B = n, то card (A ´ B)= m + n. На комбинаторном языке это означает: если объект A может быть выбран m способами, при любом выборе A объект B может быть выбран n способами, то выбор “ A и B ” может быть осуществлен m×n способами.
Пример 1. A = 10 {различных шоколадок}, B = 5 { различных пачек печенья}. Выбор “ A или B ” означает, что выбирается что-то одно и способов выбора в этом случае будет 15. Выбор “ A и B ” означает, что выбирается 1 шоколадка и 1 пачка печенья и различных вариантов для такого выбора будет 50.
Пример 2. Бросают 2 игральные кости. Сколькими способами они могут выпасть так, что на каждой кости выпадет четное число очков либо на каждой кости выпадет нечетное число очков?
Пусть m – число возможностей для выпадения четного числа на одной кости, n – число возможностей для выпадения нечетного числа. Здесь m = n = 3. По правилу произведения количество выпадения четных чисел, как и нечетных, равно 9. По правилу суммы количество возможностей для выпадения двух четных и двух нечетных чисел будет 18.
Рассмотрим основные способы формирования выборок.
Определение. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Если порядок следования элементов несущественен, то выборка называется неупорядоченной.
Из определения следует, что две упорядоченные выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, являются различными.
Перестановки. Упорядоченные выборки, объемом n из n элементов, где все элементы различны, называются перестановками из n элементов. Число перестановок из n элементов обозначается Pn.
Теорема. P = n!
Доказательство проводится по индукции. Очевидно, если n = 1, то перестановка только одна и P 1 = 1!. Пусть для n = k теорема верна и Pk = k!, покажем, что она тогда верна и для n = k +1. Рассмотрим (k +1)- й элемент, будем считать его объектом A, который можно выбрать k +1 способами. Тогда объект B – упорядоченная выборка из оставшихся k элементов по k. B соответствии с индуктивным предположением объект B можно выбрать k! способами. По принципу произведения выбор A и B можно осуществить k!(k +1) = (k +1)! способами. Совместный выбор A и B есть упорядоченная выборка из k + 1 элементов по k + 1.
Пример 3. Сколько существует способов, чтобы расположить на полке 10 различных книг? Ответ: 10!
Можно рассуждать иначе. Выбираем первый элемент, это можно сделать n способами. Затем выбираем второй элемент, это можно сделать (n - 1) способами. По правилу произведения упорядоченный выбор двух элементов можно осуществить n ´(n - 1) способами. Затем выбираем третий элемент, для его выбора останется n - 2 возможности, последний элемент можно выбрать единственным способом. Мы вновь приходим к формуле: n (n - 1)(n - r)... 1.
Размещения. Упорядоченные выборки объемом m из n элементов (m < n), где все элементы различны, называются размещениями. Число размещений из n элементов по m обозначается 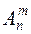 .
.
Теорема. 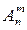 =
= 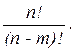
Обозначим x = 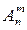 . Тогда оставшиеся (n – m) элементов можно упорядочить (n – m)! способами. По принципу произведения, если объект A можно выбрать x способами, объект B (n – m)! способами, то совместный выбор “ A и B ” можно осуществить x ×(n – m)! способами, а выбор “ A и B ” есть перестановки и Pn = n! Отсюда x =
. Тогда оставшиеся (n – m) элементов можно упорядочить (n – m)! способами. По принципу произведения, если объект A можно выбрать x способами, объект B (n – m)! способами, то совместный выбор “ A и B ” можно осуществить x ×(n – m)! способами, а выбор “ A и B ” есть перестановки и Pn = n! Отсюда x = 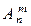 =
= 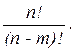
Рассуждая иначе: первый элемент выбираем n способами, второй – (n – 1) способами и т.д., m –й элемент выбираем (n – m + 1) способом. По принципу произведения вновь имеем: n (n – 1)...(n – m +1), что совпадает с 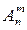 .
.
Пример 4. Группа из 15 человек выиграла 3 различных книги. Сколькими способами можно распределить эти книги среди группы?
Имеем 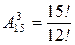 = 15 ×14 ×13 = 2730.
= 15 ×14 ×13 = 2730.
Сочетания. Неупорядоченные выборки объемом m из n элементов (m < n) называются сочетаниями. Их число обозначается 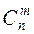 .
.
Теорема. 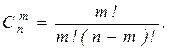
Доказательство. Очевидно, 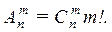 Действительно, объект A – неупорядоченная выборка из n элементов по m, их число
Действительно, объект A – неупорядоченная выборка из n элементов по m, их число 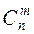 . После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “ A и B “ – упорядоченная выборка.
. После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “ A и B “ – упорядоченная выборка.
Пример 5. Группа из 15 человек выиграла 3 одинаковых книги. Сколькими способами можно распределить эти книги?
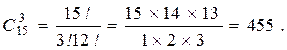
Сочетания, размещения и перестановки являлись подмножествами исходного множества. Рассмотрим выборки, которые не являются подмножествами.
Размещения с повторениями. Упорядоченные выборки объемом m из n элементов, где элементы могут повторяться, называются размещениями с повторениями. Их число обозначается 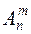 (n).
(n).
Теорема. 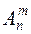 (n) = nm.
(n) = nm.
Доказательство. Первый элемент может быть выбран n способами, второй элемент также может быть выбран n способами и так далее, m -й элемент также может быть выбран n способами. По принципу произведения получаем nm.
Пример 6. Кодовый замок состоит из четырех разрядов, в каждом разряде независимо от других могут быть выбраны цифры от 0 до 9. Сколько возможных комбинаций?
Здесь n = 10, m = 4 и ответом будет 104.
Пример 7. Рассмотрим вектор длины m, каждая координата которого может принимать всего 2 значения: 0 или 1. Сколько будет таких векторов?
Это есть выборка, объемом m из двух элементов.Ответ: 2 m
Перестановки с повторениями. Пусть имеется n элементов, среди которых k 1 элементов первого типа, k 2 элементов второго типа и т.д., ks элементов s -го типа, причем k 1 + k 2 +... + ks = n. Упорядоченные выборки из таких n элементов по n называются перестановками с повторениями, их число обозначается Cn (k 1, k 2,..., ks). Числа Cn (k 1, k 2,..., k s) называются полиномиальными коэффициентами.
Теорема. Cn(k1,..., ks)= 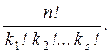
Доказательство проведем по индукции по s, т. е. по числу типов элементов. При s = 1 утверждение становится тривиальным: k 1 = n, все элементы одного типа и Cn (n) = 1. В качестве базы индукции возьмем s = 2, n = k 1 + k 2. В этом случаем перестановки с повторениями превращаются в сочетания из n элементов по k 1 (или k 2): выбираем k 1 место, куда помещаем элементы первого типа.
Cn (k 1, k 2) = 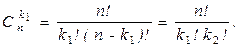
Пусть формула верна для s = m, т.е. n = k 1 +... + km и
Cn(k 1,..., km)= 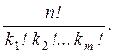
Докажем, что она верна для s = m + 1 (n = k 1 +... + km + km +1). В этом случае перестановку с повторениями можно рассматривать как совместный выбор двух объектов: объект A – выбор k m + 1 места для элементов (m + 1)-го типа; объект B – перестановка с повторениями из (n – km +1) элементов. Объект A можно выбрать 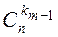 способом, B –
способом, B – 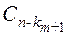 (k 1,..., k m) способами. По принципу произведения
(k 1,..., k m) способами. По принципу произведения
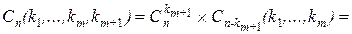
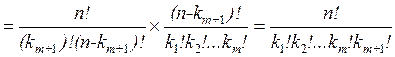
и мы получили требуемую формулу.
Замечание. Числа 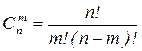 называются биноминальными коэффициентами. Из этой формулы следует, что
называются биноминальными коэффициентами. Из этой формулы следует, что 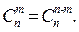
Пример 8. Сколько различных слов можно получить, переставляя буквы в слове “математика”?
Решение. Буква “а” входит 3 раза (k 1= 3), буква “м” – 2 раза (k 2 = 2), “т” – 2 раза (k 3 = 2), буквы “е”, ”к”, ”и” входят по одному разу, отсюда k 3 = k 4 = k 5 = 1.
C 10 (3, 2,, 2, 1, 1, 1) = 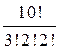 =151200.
=151200.
Сочетания с повторениями. Пусть имеется n типов элементов, каждый тип содержит не менее m одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³ m ´ n) называется сочетанием с повторением. Число сочетаний с повторениями обозначается 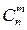 (n).
(n).
Теорема. 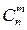 (n) =
(n) = 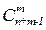 .
.
Доказательство. Пусть в выборку вошло m 1 элементов первого типа, m 2 элементов второго типа,... m n – n -го типа. Причем каждое 0 £ m i £ m и m 1+ m 2+...+ mn = = m. Сопоставим этой выборке вектор следующего вида: 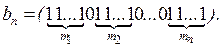 Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов { bn } существует биекция (докажите это!). Следовательно,
Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов { bn } существует биекция (докажите это!). Следовательно, 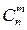 (n) равно числу векторов bn. “ Длина вектора” bn равна числу 0 и 1, или m + + n– 1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n - 1 мест, а это будет
(n) равно числу векторов bn. “ Длина вектора” bn равна числу 0 и 1, или m + + n– 1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n - 1 мест, а это будет 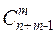 .
.
Пример 9. В кондитерской имеется 7 видов пирожных. Покупатель берет 4 пирожных. Сколькими способами он может это сделать? (Предполагается, что пирожных каждого вида ³ 4).
Число способов будет 
Пример10. Пусть V = { a, b, c }. Объем выборки m = 2. Перечислить перестановки, размещения, сочетания, размещения с повторениями, сочетания с повторениями.
1. Перестановки: { abc, bac, bca, acb, cab, cba }. P 3=3!=6.
2. Размещения: {(ab), (bc), (ac), (ba), (cb), (ca)}. 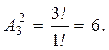
3. Сочетания: {(ab), (ac), (bc)}. 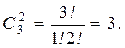
4. Размещения с повторениями: {(ab), (bc), (ac), (ba), (cb), (ca), (aa), (bb), (cc)}. 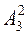 (3)= 32 = 9.
(3)= 32 = 9.
5. Сочетания с повторениями: {(ab), (bc), (ca), (aa), (bb), (cc)}. 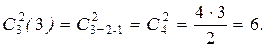
Date: 2015-04-23; view: 3376; Нарушение авторских прав