Характеристики атмосферного влажного воздуха

При температурах атмосферного воздуха 0-50 ^оС парциальное давление водяного пара очень мало (0,006-0,07 бар), что позволяет применить к перегретому и сухому насыщенному водяному пару уравнение идеального газа:

Р_пv = RT, (7.3)

Р_нv" = RT, (7.4)

где Р_п, Р_н и v, v" – парциальные давления и удельные объемы для перегретого и сухого насыщенного водяного пара при температуре Т.

Разделив эти выражения друг на друга, получим расчетное выражение относительной влажности воздуха через парциальные давления водяного пара:

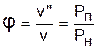. (7.5)

Молярная масса атмосферного влажного воздуха определяется по уравнению для смеси газов:

m = r_вm_в + r_пm_п, (7.6)

где r_в, r_п – объемные доли сухого воздуха и водяного пара,

r_в = Р_в/Р=(Р - Р_п)/Р; r_п = Р_п/Р,

Р, Р_в и Р_п – атмосферное и парциальные давления сухого воздуха и водяного пара;

m_в, m_п – молярные массы сухого воздуха и водяного пара,

m_в=28,96 кг/кмоль, m_п=18,016 кг/кмоль.

В результате подстановки численных значений молярных масс сухого воздуха и водяного пара в выражение (7.6) получаем расчетное выражение молярной массы влажного воздуха в виде

. (7.7)

Молярная масса влажного воздуха меньше молярной массы сухого воздуха.

Газовая постоянная влажного воздуха определяется выражением

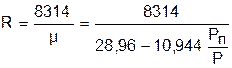, (7.8)

онабольше газовой постоянной сухого воздуха.

Плотность влажного воздуха определяется выражением

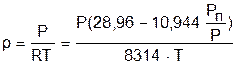, (7.9)

онаменьше плотности сухого воздуха, т.е. влажный воздух легче сухого воздуха.

Влагосодержание d – это масса водяного пара в граммах, приходящаяся на 1 кг сухого воздуха. В общем случае понятие "влагосодержание" относится не только к паровой фазе воды, но и к жидкой, и к твердой ее фазам. Расчетное выражение для влагосодержания паровой фазы воды в воздухе (г/кг с.в.) получается из соотношения

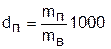(7.10)

путем замены отношений масс на массовые доли и выражения последних через объемные доли, которые представляют отношения соответствующих парциальных давлений к давлению всей смеси:

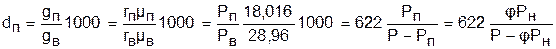, (7.11)

где g_п, g_в – массовые доли пара и сухого воздуха;

r_п, r_в – объемные доли пара и сухого воздуха.

Энтальпия влажного воздуха Н рассчитывается на 1 кг сухого воздуха (кДж/кг с.в.) и определяется как сумма энтальпий компонентов, находящихся в 1 кг сухого воздуха:

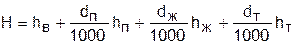, (7.12)

где d_п, d_ж, d_т – количество пара, жидкости и твердой фазы Н₂О (лед, снег) в граммах на 1 кг сухого воздуха (влагосодержания);

h_в, h_п, h_ж, h_т – удельные энтальпии сухого воздуха, пара, жидкости и твердой фазы Н₂О, кДж/кг.

В выражении (7.12) энтальпии всех компонентов влажного воздуха необходимо подставлять при одинаковых давлениях и температурах начала их отсчета.

Для атмосферного влажного воздуха удельные энтальпии всех компонентов можно рассчитать, приняв ряд допущений, которые не приведут к погрешностям инженерных расчетов в диапазоне изменения атмосферного давления и температуры от -40 до 150 ^оС более чем на 0,5 %.

Эти допущения сводятся к следующему.

Начало отсчета удельной энтальпии сухого воздуха принимают при t_о=0 ^оС и считают, что энтальпия сухого воздуха зависит только от температуры (как для идеального газа), а его изобарная теплоемкость – величина постоянная. Расчетное выражение удельной энтальпии сухого воздуха в этом случае будет соответствовать соотношению

h_в = h_в - h_во = c_рв(t - 0) = с_рвt, (7.13)

где h_во = 0 – начало отсчета энтальпии сухого воздуха при 0 ^оС;

c_рв = 1 кДж/(кг∙К) – изобарная теплоемкость идеального сухого воздуха, принята постоянной.

При таких допущениях удельная энтальпия сухого воздуха (кДж/кг) численно равна его температуре в градусах Цельсия:

h_в = t.

Для определения энтальпии воды и водяного пара начало отсчета внутренней энергии u_о = 0 принято при параметрах тройной точки воды (t_o=0,01 ^оС и Р_o=611,2 Па) на линии насыщения х=0. При этих параметрах численное значение энтальпии h_о' = P_ov_o' = 0,000611 кДж/кг представляет очень малую величину, которую для наших расчетов можно принять равной нулю. Таким образом, можно считать, что начало отсчета энтальпии H₂О, как и сухого воздуха, ведется от 0 ^оС и ее численное значение при этой температуре равно нулю (h_по=0).

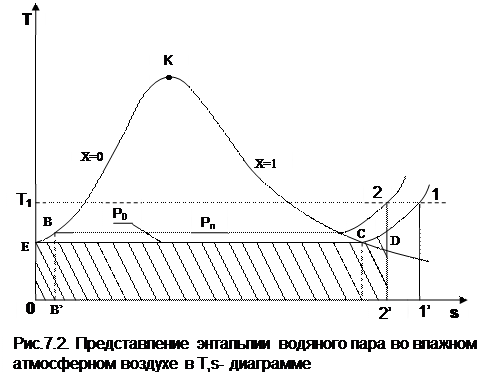
Для дальнейшего пояснения определения энтальпии водяного пара рассмотрим изобару Р_o, соответствующую тройной точке воды в Т,s- диаграмме (рис.7.2). Площадь ЕС11'0Е под изобарой Е1 представляет в T,s- диаграмме теплоту изобарного процесса, состоящую из теплоты парообразования и теплоты перегрева пара, которая рассчитывается как разность энтальпий:

h_п1 - h_по = r_о + q_п1.

Поскольку энтальпию в тройной точке воды (точка Е) мы приняли за нуль, то абсолютное значение удельной энтальпии пара в точке 1 определяется выражением

h_п1 = r_o + q_п1,

где r_o = 2501 кДж/кг – теплота парообразования воды при 0 ^оС;

q_п1 – теплота перегрева пара от Т_о до Т.

Приняв изобарную теплоемкость перегретого пара величиной постоянной, c_рп=1,93 кДж/(кг∙К), что допустимо для интервала температур атмосферного воздуха, получим расчетное выражение теплоты перегрева пара (кДж/кг):

q_п1 = с_pп(t - 0) = 1,93t.

В результате этих преобразований расчетное выражение энтальпии водяного пара при температуре t и давлении тройной точки воды Р_o примет вид (кДж/кг)

h_п1 = 2501 + 1,93t.

Этим выражением можно пользоваться и для расчета энтальпий пара при давлениях, отличных от давления тройной точки воды. Это объясняется тем, что при атмосферных условиях парциальные давления пара малы и близки к давлению тройной точки воды. При Р_п>Р_о (соответствует состоянию пара в точке 2, рис.7.2) энтальпия пара будет представлять сумму трех слагаемых:

h_п = q' + r + q_п,

Энтальпии пара h_п соответствует площадь под изобарой ЕВ2. По сравнению с площадью под изобарой Е1 здесь присутствует теплота q', но величины r и q_п уменьшились по сравнению с величинами r_o и q_п1. При малых отклонениях изобар от изобары тройной точки воды в выражении для h_п по сравнению с выражением для h_п1 будет происходить взаимная компенсация уменьшения величин r и q_п за счет увеличения величины q'. В соответствии с рис. 7.2 эту взаимную компенсацию составляющих энтальпий h_п и h_п1 можно представить равенством площадей 11'2'D1 и 2DCЕВ2, т.е. будет справедливо равенство энтальпий h_п1 и h_п. На основании этого равенства получается расчетное выражение для энтальпии пара в атмосферном влажном воздухе:

h_п = r_o + q_п1 = q' + r + q_п = 2501 + 1,93t. (7.14)

Для определения энтальпии жидкой фазы воды принимают постоянной ее изобарную теплоемкость, что допустимо при параметрах атмосферного воздуха. Исходя из этого допущения расчетное выражение энтальпии жидкой фазы воды будет представлено в виде уравнения

h_ж = h_ж - h_по = с_рж(t - 0) = 4,187t, (7.15)

где с_рж = 4,187 кДж/(кг∙К) – изобарная теплоемкость воды.

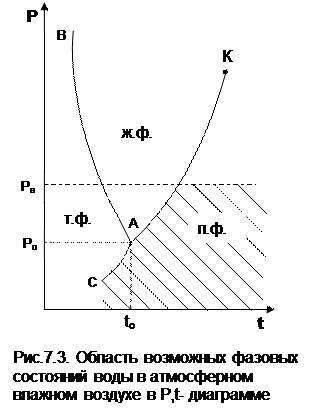
Для определения энтальпии твердой фазы воды (лед, снег) принимаются постоянными удельная теплота плавления льда и его изобарная теплоемкость. Эти величины берутся при параметрах тройной точки воды. Такие допущения возможны, поскольку в соответствии с Р,t- диаграммой для воды (рис.7.3) имеют место следующие факты:

· в атмосферном воздухе твердая фазы воды (т.ф.) может присутствовать только при температурах и парциальных давлениях пара, меньших (или равных) температуры и давления тройной точки воды, т.к. только на линии сублимации АС возможно одновременное существование паровой и твердой фаз воды;

· плавление льда в атмосферном воздухе возможно только при температуре 0 ^оС;

· переход льда в паровую фазу при температурах меньше 0 ^оС происходит, минуя жидкую фазу воды, – по линии сублимации (АС);

· парциальное давление водяного пара при отрицательных температурах атмосферного воздуха ненамного меньше (или равно) давления тройной точки воды Р_о, следовательно, теплота изобарного охлаждения твердой фазы воды от 0 ^оС может быть рассчитана по изобаре Р_о.

Энтальпия льда будет величиной отрицательной, поскольку начало отсчета энтальпии идет от температуры 0 ^оС жидкой фазы воды, а температура льда всегда меньше или равна 0 ^оС. Расчетное выражение энтальпии твердой фазы воды (льда, снега) в атмосферном воздухе представляет собой сумму удельной теплоты плавления льда, взятой с отрицательным знаком, и удельной изобарной теплоты охлаждения льда от t=0 ^оС до отрицательной температуры t:

h_т = - l + с_рт(t - 0) = -335 + 2,1t, (7.16)

где l = 335 кДж/кг – удельная теплота плавления льда при t=0 ^оС;

с_рт = 2,1 кДж/(кг∙К) – изобарная теплоемкость льда; взята при давлении тройной точки воды и принята величиной постоянной.

В результате всех вышеприведенных упрощений окончательное расчетное выражение энтальпии влажного атмосферного воздуха (кДж/кг с.в.) примет вид

. (7.17)

Date: 2015-05-09; view: 880; Нарушение авторских прав