Энтропия и ее свойства

Используя формулы (8.38) и (8.40), можно получить выражение:

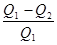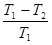£ , (8.41)

где Q₁ – количество теплоты, которую нагреватель отдает рабочему телу; Q₂ – количество теплоты, которую забирает холодильник; T₁ – температура нагревателя; T₂ – температура холодильника. Здесь знак “=” отвечает обратимым, а знак “< “ – необратимым процессам.

Рассмотрим обратимый цикл Карно, для которого выражение (8.41) можно записать как:

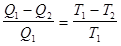, (8.42)

или

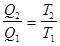, (8.43)

откуда:

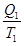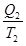– = 0. (8.44)

Поскольку Q₂ отдается рабочим телом холодильнику, то Q₂< 0, и последнее уравнение можно записать:

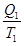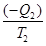– = 0, (8.45)

или

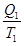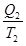+ = 0. (8.46)

Отношение теплоты к абсолютной температуре называется приведенной теплотой. Таким образом, сумма приведенных теплот при обратимом цикле Карно равна нулю.

Любой круговой процесс можно представить как большое число элементарных циклов Карно (рис. 8.15):

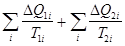= 0. (8.47)

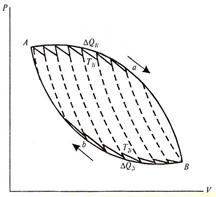
Рис. 8.15. Круговой процесс как бесконечное число элементарных циклов Карно

Если перейти от бесконечного числа элементарных циклов Карно, то суммы в последней формуле преобразуются в интегралы:

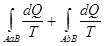= 0, (8.48)

или

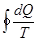= . (8.49)

Подынтегральное выражение 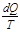представляет собой полный дифференциал функции S, которая зависит от состояния системы и не зависит от пути, которым системы пришла к этому состоянию; она определяется лишь начальным и конечным состояниями обратимого процесса:

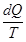= dS. (8.50)

Функция S називается энтропией. Этот термин, который происходит от греческого слова troph (преобразование), был впервые использован Клаузиусом в 1865 г. Измеряется энтропия в Дж/К.

Изменение энтропии определяется суммарным значением поглощенных системой приведенных теплот. При бесконечно малых изменениях состояния системы изменение энтропии dS равно (во время обратимых процессов) или превышает (во время необратимых процессов) значения поглощенной системой элементарной приведенной теплоты (неравенство Клаузиуса).

Итак, для обратимых процессов справедливы такие выражения:

dS = 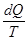; 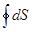= = 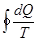, (8.51)

а для необратимых - такие:

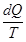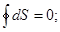
dS > ; 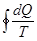< 0. (8.52)

Во время произвольных процессов изолированная система переходит в состояние термодинамического равновесия, которое характеризуется максимальной энтропией.

Таким образом, основные тенденции изменения энтропии можно сформулировать так:

1. В изолированной системе, в которой проходят обратимые процессы, энтропия сохраняет постоянное значение:

dS = 0; S = const. (8.53)

2. В изолированной системе, в которой проходят необратимые процессы, энтропия возрастает:

dS > 0. (8.54)

3. При термодинамическом равновесии энтропия стремится к максимальному значению:

S ® S_max. (8.55)

Второй закон термодинамики для необратимых процессов показывает направление процесса: необратимые процессы всегда происходят в направлении возрастания энтропии. Следовательно, можно ввести еще одно определение энтропии: это такая функция состояния системы, которая определяет направление протекания произвольного процесса: в изолированной системе энтропия сохраняет постоянное значение во время обратимых процессов, возрастает при необратимых процессах и достигает максимального значения в случае термодинамического равновесия.

Пример

Определить изменение энтропии в процессе плавления 2 кг льда, температура которого 0 ⁰С.

Date: 2015-05-09; view: 964; Нарушение авторских прав