Исследование уравнения Ван-Дер-Ваальса

Преобразуем формулу (3.1), раскрыв скобки и умножив обе части равенства на V²/p:

,

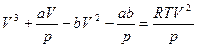далее расположим слагаемые в порядке убывающих степеней V:

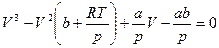. (3.3)

Полученное выражение является кубическим уравнением относительно объема[5].

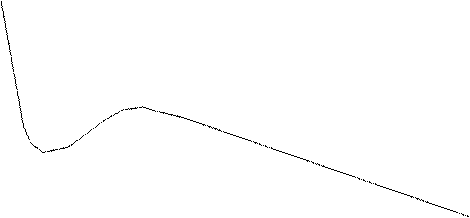
Зададимся некоторой определенной температурой T и для нее построим график, выражающий связь V и p по формуле (3.3). Будем давать p, например 1 атм, 1, 5, 2, 2,5 атм и.т.д. Подставляя вместо p его значения, будем получать кубическое уравнения с численными коэффициентами (a, b, R - табличные данные, T - заданная температура). Если для V получится один вещественный корень, соответствующий данному p, на графике будет точка с координатами (p,V). Если при решении уравнения окажутся три вещественных корня, данному давлению будут соответствовать три возможных объема (V₁, V₂, V₃) и кривая, изображающая графически уравнение (3.3), очевидно, будет иметь перегибы. В результате изотерма Ван-Дер-Ваальса примет вид, изображенный на рис. (3.4). Ее участок 1-2 соответствует такому же участку, полученному экспериментальным путем на изотерме Эндрюса. Это состояние ненасыщающего пара. Участок 2-3 на опыте получается в виде прямой, на изотерме же Ван-дер-Ваальса - кривая 2-2'-3'-3. Несовпадение этого участка графика с опытными данными не является неожиданным, так как он соответствует состоянию насыщающего пара, для которого формула Клайперона - Менделеева неприменима (уравнение Ван-дер-Ваальса есть подправленная форма уравнения состояния идеального газа). Однако участки 2-2' и 3-3' при известных условиях могут быть получены на опыте и только участок 2'-3' экспериментально неосуществим. Если осторожно сжимать сначала ненасыщенный пар, а затем после достижения его насыщения (точка 2) продолжать сжатие, при отсутствии в нем ионов и пылинок, которые являются центрами конденсации, можно получить участок 2-2', соответствующий пресыщающему пару. Его давление не может превысить p₁; достигнув его, пресыщающий пар начинает бурно конденсироваться, давление падает до p_н и

p 4

2΄

2

3

3΄

p₂ p₁ p_н

1

0 V

Рис. 3.4. Изотерма Ван-Дер-Ваальса

дальше (до точки 3) не изменяется. Если постепенно уменьшать давление на сжатую жидкость и продолжать осторожно приподнимать поршень в цилиндре, достигнув при этом давления, соответствующего точке 3', то можно несколько перегреть или <<растянуть>> жидкость и получить экспериментально участок изотермы 3'-3. При достижении газом точки 3' поршень отрывается от жидкости, давление от значения p₂ возрастает до значения p_н вследствие интенсивного парообразования. Участок 3-4 характеризует жидкую фазу.

На рис. (3.5) показан ряд изотерм Ван-дер-Ваальса, построенных для различных температур. Изотерма T_к соответствует критической температуре. Изотермы, расположенные выше нее (для более высоких температур), характеризуются тем, что вещество при этих температурах остается в газообразном состоянии и ни при каком давлении не может быть обращено в жидкость. Для точки K можно найти значение V_к, подставив в уравнение (3.3) значения критического давления p_к и критической температуры T. В этом случае формула принимает вид:

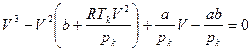. (3.4)

С другой стороны, любое кубическое уравнение, имеющие корни V₁, V₂, V₃, можно записать в виде:

(V-V₁)(V-V₂)(V-V₃)=0. (3.5)

Но для точки K все три корня сливаются в один, т.е. V₁=V₂=V₃=V_к и последнее соотношение принимает вид:

(V-V_k)³=0.

р

р_к К

0 V_k V

Рис. 3.5. Изотермы Ван-Дер-Ваальса, соответствующие температурам, близким к критической

Раскрывая скобки, его можно привести к виду:

V³-3V_kV²+3V_kV-V_k³=0. (3.6)

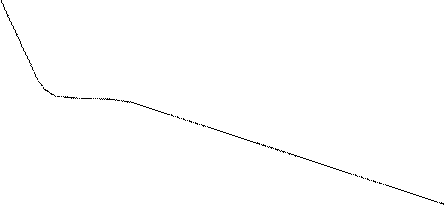
Так как уравнения (3.4) и (3.6) являются тождественными, их коэффициенты при одинаковых степенях неизвестных должны быть равны. Поэтому можно записать:

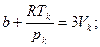
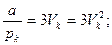
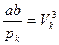. (3.7)

Эти уравнения связывают между собой шесть величин. Зная три из них, остальные три можно найти. Например, можно теоретически подсчитать критические параметры V_к, p_к, T_к по известным a, b, R. И, наоборот, зная V_к, p_к, T_к, можно найти постоянные Ван-дер-Ваальса a и b:

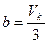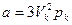, . (3.8)

Характерно, что критический объем оказывается равным утроенной постоянной b. Однако эти соотношения являются приближенными. В некоторых таблицах критических параметров значение критического объема не приводится. Поэтому приведем выражение параметров Ван-Дер-Ваальса a и b через p_к, T_к:

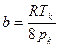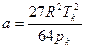, . (3.9)

Т а б л и ц а 3.3

Удельная теплота парообразования воды при разных температурах

Предлагаем вам получить эти выражения из (3.7) самостоятельно.

Date: 2015-05-09; view: 800; Нарушение авторских прав