Основы теории. Идеальным газом называется воображаемый газ, молекулы которого представляют собой материальные точки

Идеальным газом называется воображаемый газ, молекулы которого представляют собой материальные точки, не имеющие собственного объема и не взаимодействующие между собой. Зависимость между основными термодинамическими параметрами такого газа определяется уравнением состояния идеального газа – уравнением Клапейрона-Менделеева:

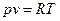, (1)

где 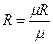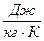- газовая постоянная;

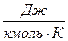- универсальная газовая постоянная.

Реальные газы состоят из молекул, имеющих конечный собственный объем, между которыми действуют силы межмолекулярного взаимодействия (силы притяжения и отталкивания). Эти газы описываются уравнением (1) только при малых плотностях, когда среднее расстояние между центрами молекул сравнительно велико и эти силы не проявляются. В более плотных реальных газах со значительно меньшим расстоянием между молекулами необходимо учитывать и силы взаимодействия, и собственный объем молекул. Поведение реальных газов качественно отражает уравнение Ван-дер-Ваальса:

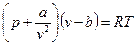, (2)

где 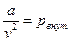- внутреннее (молекулярное) давление, возникающее за счет действия сил притяжения и отталкивания между молекулами (для жидкостей оно велико);

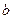- наименьший объем, до которого можно сжать газ, обусловленный собственным объемом молекул.

Тогда 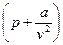представляет собой полное давление системы, а 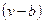– свободный объем.

Для количественных расчетов уравнение (2) часто малопригодно, т.к. при высоких плотностях, а следовательно, при высоких давлениях параметры, рассчитанные по этому уравнению, расходятся с действительными (экспериментальными) значениями.

Уравнение Ван-дер-Ваальса можно представить в приведенных параметрах состояния. Если переменные p, v и T отнести к их значениям в критической точке 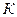(далее в опыте Эндрюса эта точка будет рассмотрена подробнее), то можно получить приведенные значения объема 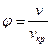, давления 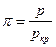и температуры 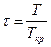и записать так называемое приведенное уравнение состояния:

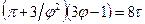. (3)

Состояния веществ, находящихся при одинаковых 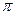, 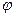и , называются соответственными состояниями.

Уравнения типа (2) и (3) получаются в случае, если ограничиться рассмотрением только парных взаимодействий между молекулами, т.е. в группах по две молекулы. Поэтому эти уравнения применимы в области не очень высоких давлений.

С повышением давления необходимо учитывать образование устойчивых молекулярных ассоциаций из трех, четырех и более молекул, распад которых возможен только при подводе энергии извне, т.е. при нагревании. Такой газ можно рассматривать как «смесь» нескольких газов, частицами которых являются одиночные, двойные, тройные и т.д. группы молекул [4, 5].

Уравнение состояния реальных газов формально можно записать в виде:

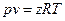, (4)

где z - коэффициент сжимаемости или неидеальности (для идеальных газов z = 1) - можно представить в виде вириального уравнения, учитывающего и взаимодействия более высокого порядка:

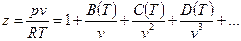. (5)

Правую часть этого уравнения можно рассматривать как разложение в ряд коэффициента z по степеням плотности 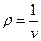. Зависящие от температуры функции 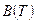, , 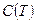… выступают здесь как вириальные (от латинского viris - силы) коэффициенты, учитывающие соответственно парные, тройные, четверные и т.д. взаимодействия. Область справедливости вириального разложения ограничивается сходимостью рядов. Ряды расходятся при плотностях, соответствующих жидкому состоянию. Уравнение (5) оказывается справедливым для газов умеренной плотности. Расчеты вириальных коэффициентов достаточно сложны и поэтому уравнение (5) используется, в основном, при проведении научных исследований.

Коэффициент неидеальности z может быть найден также по зависимости 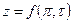из 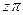- диаграммы (рис.1).

Рассчитанное значение 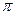откладывается на соответствующей оси этой диаграммы и из этой точки проводится прямая, перпендикулярная оси 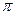до пересечения с кривой, соответствующей рассчитанному значению t. Точка пересечения позволяет определить искомую величину коэффициента неидеальности на оси z.

Точность расчетов в этом случае окажется такой же, как и по уравнению Ван-дер-Ваальса (2) или приведенному уравнению (3).

Date: 2015-05-09; view: 746; Нарушение авторских прав