Расчетные формулы энергии Гиббса и энергии Гельмгольца

· Стандартная энергия Гиббса реакции равна сумме стандартных энергий Гиббса продуктов реакций за вычетом суммы стандартных энергий Гиббса исходных веществ с учетом стехиометрических коэффициентов уравнения реакции.

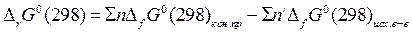(63)

где 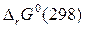- стандартная энергия Гиббса реакции,

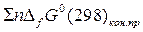- сумма стандартных энергий Гиббса продуктов реакции,

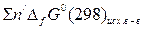- сумма стандартных энергий Гиббса исходных веществ,

n, n^/ - стехиометрические коэффициенты исходных веществ и конечных продуктов в уравнении реакции.

Стандартные значения энергии Гиббса для 1 моля вещества при Т = 298 К приведены в справочнике /5, табл.44; 6, табл.1/.

Пример 1. Рассчитать стандартные энергии Гиббса и Гельмгольца реакции, используя значения стандартных энергий Гиббса, приведенных в справочнике /5, табл.44/:

.

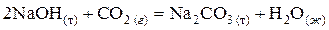Решение:

1) Расчет энергии Гиббса.

Находим в справочнике /5, табл.44/ значения стандартных энергий Гиббса для веществ реакции:

а) продукты реакции

,

,

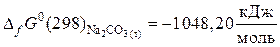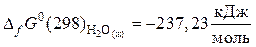б) исходные вещества

,

.

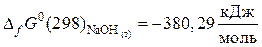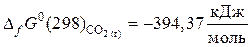Применяя уравнение (63), получим:

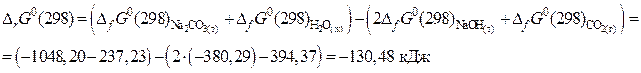
Вывод. Полученное значение энергии Гиббса (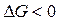) указывает на то, что данная реакция в закрытой системе может протекать в стандартных условиях в прямом направлении.

2) Расчет энергии Гельмгольца.

Для расчета изохорно-изотермического потенциала рассмотрим соотношение между энергией Гиббса и энергией Гельмгольца:

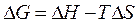, , но .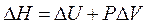

Тогда:

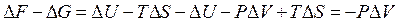, (64)

т.е.

Если в реакции принимают участие только конденсированные фазы (твердые и жидкие вещества), то изменение объема DV равно нулю.

Если в реакции участвуют газообразные продукты, то изменением объема пренебрегать нельзя.

Рассмотрим простейший случай, когда газы, участвующие в реакции, подчиняются законам идеального газа. Тогда согласно уравнению Клапейрона-Менделеева можно записать PDV=DnRT.

Dn=n _кон - n _исх,

где n _кон - число молей газообразных конечных продуктов;

n_исх – число молей газообразных исходных веществ.

В нашем примере газообразный продукт один – углекислый газ, поэтому Dn = 0 - 1= - 1.

Тогда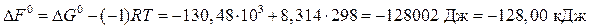

Вывод. Т.к. полученное в результате расчета значение DF <0, то в изохорно-изотермическом процессе в закрытой системе будет протекать самопроизвольный процесс.

· Для нахождения энергии Гиббса можно применять уравнение (56), которое дает возможность производить расчет как в стандартных условиях, так и при любой другой температуре.

Пример 2. Вычислить энергию Гиббса и Гельмгольца при Т ₁ = 298 К и Т ₂ = 473 К, при постоянном давлении 1,013×10⁵ Па для реакции:

.

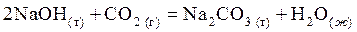Как скажется повышение температуры на направления протекания данной реакции?

Решение. Для расчета DG реакции воспользуемся уравнением (56):

,

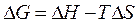где DH и DS - соответственно изменение энтальпии и энтропии реакции при заданной температуре:

а) Т =298 К.

Определяем изменение стандартной энтальпии реакции D_rH⁰ (298) (расчет приведен в примере 1 раздела 1.3.3): D_rH⁰ (298) = -170,42 кДж.

Определяем изменение стандартной энтропии реакции D_rS⁰ (298) (расчет приведен в примере 1 раздела 1.5.4): D_rS⁰ (298) = -133,77 Дж.

Подставим полученные данные в уравнение (56):

.

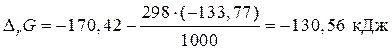Вывод. Расчет стандартной энергии Гиббса по справочным данным, приведенный в предыдущем примере, и расчет по уравнению (56), приведенный в данном примере, практически совпадают. Относительная ошибка составляет:

.

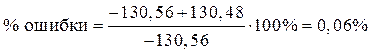Расчет DF (298) см. в этом же разделе, пример 1.

б) Т = 473 К.

Определяем изменение энтальпии реакции D_rH (473) (расчет приведен в примере 2 раздела 1.4.2):

D_rH (473) = -125,79 кДж.

Определяем изменение энтропии реакции D_rS (473) (расчет приведен в примере 1 раздела 1.5.4):

D_rS (473) = -12,9 Дж.

Подставим полученные данные в уравнение (56):

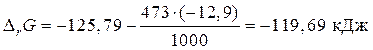
Расчет DF проводим согласно уравнению (64):

.

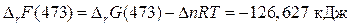Вывод. Ответ на последний вопрос задачи определяется знаком D_rS и D_rH (см. табл. 1). В нашем случае 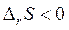, т.е. в уравнении 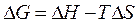член (- TDS) для нашей реакции положителен. Следовательно, с повышением температуры Т в изобарно-изотермическом процессе значение D_rG будет возрастать (т.е. становиться менее отрицательным). Это означает, что повышение температуры будет препятствовать протеканию рассматриваемой реакции в прямом направлении.

В изохорно-изотермическом процессе будут наблюдаться аналогичные тенденции для энергии Гельмгольца.

· Можно рассчитать D_rG, воспользовавшись уравнением (60), если в химическом процессе давление остается неизменным. Для химической реакции это уравнение примет вид:

.

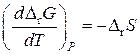Преобразуем данное уравнение 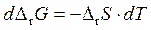и проинтегрируем:

.

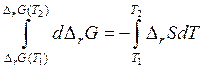Если Т₁ = 298 К, то уравнение примет вид:

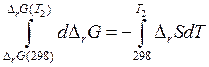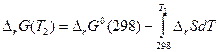или (65)

В зависимости от степени точности возможны три варианта расчета энергии Гиббса по этому способу.

Первый вариант. Предположим, что энтропия реакции не зависит от температуры, т.е. D_rS⁰ (298) = D_rS (Т₂), тогда:

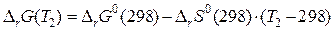. (66)

Полученный результат расчета дает существенную погрешность.

Пример 3. Вычислить энергию Гиббса предложенным способом для реакции:

.

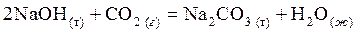При Т ₂ = 473 К, при постоянном давлении 1,013×10⁵ Па.

Решение.

Стандартную энергию Гиббса находим по уравнению (63) (см. пример 1 в разделе 1.5.8.): D_rG⁰ (298) = -130,48 кДж.

Определяем изменение стандартной энтропии реакции D_rS⁰ (298) (расчет приведен в примере 1 раздела 1.5.4): D_rS⁰ (298) = -133,77 Дж.

Подставим полученные данные в уравнение (66) и произведем расчет: .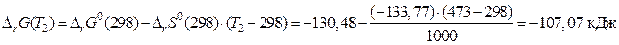

Вывод. Результат расчета отличается от результата в примере 2,б раздела 1.5.8, т.к. последний вариант является приближенным, не учитывается фазовый переход воды.

Второй вариант. Предположим, что энтропия реакции зависит от температуры

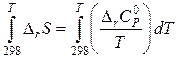или .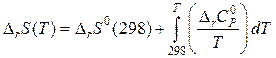

Если теплоемкость не зависит от температуры D_rС_Р = const, то после интегрирования имеем:

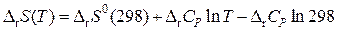D.

Подставим полученное значение D _r S (Т)в (65):

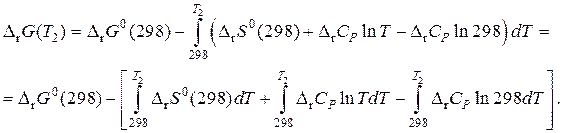
После интегрирования получим:

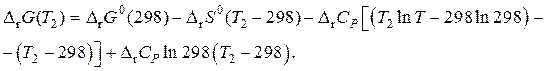(67)

Пример 4. Рассчитать изменение энергии Гиббса при Т = 473К реакции:

,

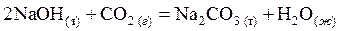учитывая зависимость энтропии реакции от температуры.

Решение.

Определяем D _r С_Р реакции по первому следствию закона Гесса:

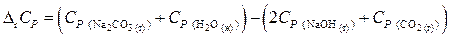
Воспользуемся значениями стандартных изобарных теплоемкостей для индивидуальных веществ, приведенных в справочнике /5, табл. 44/:

а) продукты реакции:

,

;

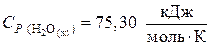б) исходные вещества:

,

.

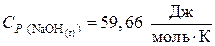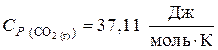Тогда .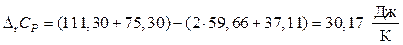

Расчет стандартной энергии Гиббса для данной реакции приведен в примере 1 раздела 1.5.8. D_rG⁰ (298) = -130,48 кДж.

Расчет стандартной энтропии для данной реакции приведен в примере 1 раздела 1.5.4. D_rS⁰ (298) = -133,77 Дж.

Подставляя полученные значения в (67), получим:

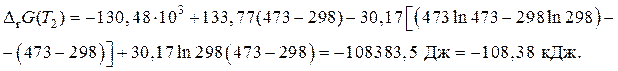
Вывод: данный расчет также является приближенным, т.е. он не учитывает зависимость теплоемкости от температуры, но более точным, чем первый способ, рассмотренный выше.

Пример, рассматриваемый нами, является более сложным, т.к. в предложенном интервале температур у одного из веществ, а именно у воды, существует фазовый переход, что необходимо учитывать. Это усложняет расчет и делает его громоздким.

В таких случаях вычислить энергию Гиббса можно, воспользовавшись формулой (56). Расчет этот приведен в примере 2 раздела 1.5.8.

На практике часто для расчета энергии Гиббса используют метод Темкина - Шварцмана (1946 г.), позволяющий стандартную энергию Гиббса при 298 К пересчитать для любой температуры /1, 4, 7, 8/.

Пример 5. Вычислить изменение энергии Гиббса при изотермическом сжатии 0,005 м³ кислорода от Р₁ =0,1013×10⁵ Па до Р₂ =1,013×10⁵ Па (Т = 0⁰С), считая кислород идеальным газом.

Решение. Из уравнение Менделеева-Клапейрона находим число молей кислорода, участвующих в реакции:

PV=nRT,

:

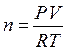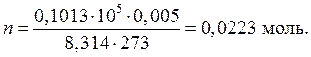
Для определения DG воспользуемся формулой (58):

.

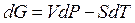Т.к. процесс протекает при Т= const, то второе слагаемое будет равно нулю. Расчет проводим по формуле dG = VdP.

Из уравнения Менделеева-Клапейрона выразим V:

.

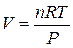Подставляем:

.

Интегрируем и подставляем данные задачи:

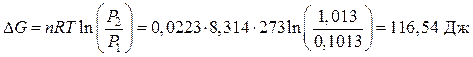
Вывод. При изотермическом сжатии кислорода процесс не может протекать самопроизвольно.

Пример 6. Теплота плавления льда при 0⁰С равна 335 Дж/г. Удельная теплоемкость воды равна 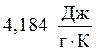. Удельная теплоемкость льда равна 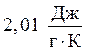. Найти DG, DH, DS для процесса превращения 1 моль переохлажденной воды при – 5⁰С в лед.

Решение. Переохлажденная жидкость не находится в состоянии равновесия с твердой фазой. Рассматриваемый процесс не является статическим, поэтому вычислить энтальпию и энтропию по теплоте кристаллизации для переохлажденной жидкости нельзя.

Для вычисления данных функций мысленно заменим нестатический процесс тремя квазистатическими, в результате которых система придет из начального состояния в конечное.

1-й процесс. Нагревание обратимым путем 1 моль воды до температуры замерзания. При этом изменение энтальпии и энтропии согласно уравнениям (26) и (36):

,

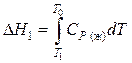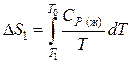
где С_Р – молярная теплоемкость воды,

.

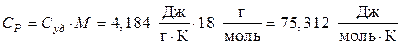Подставляя в формулы данные задачи, получим:

,

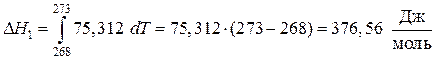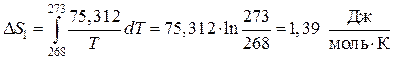
2-й процесс. Кристаллизация воды при 0⁰С (273 К). В условиях задачи дана удельная теплота плавления (DН _плавл), т.е. теплота фазового перехода 1 г воды из твердого состояния в жидкое.

Т.к. ,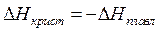

то ,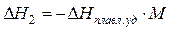

где DН₂ – теплота кристаллизации 1 моля воды,

DН _{плавл. уд} – удельная теплота плавления, приведенная в задаче,

М – молярная масса воды.

Тогда .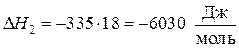

Энтропия фазового перехода рассчитывается по формуле (47):

.

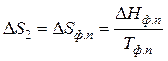Подставим данные и получим:

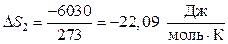
3-й процесс. Обратимое охлаждение льда от 273 до 268 К. Расчет энтальпии и энтропии проводим аналогично первому процессу.

, ,

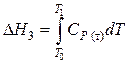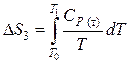где С_Р – молярная теплоемкость льда,

.

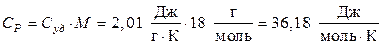Подставляя данные, получим:

,

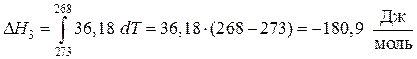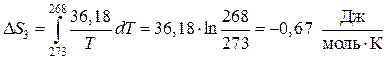
Общее изменение энтальпии и энтропии в изобарном процессе

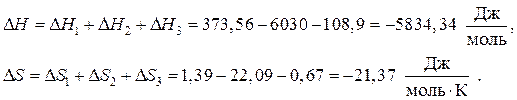
Изменение энергии Гиббса в рассматриваемом процессе рассчитывается по формуле (56).

.

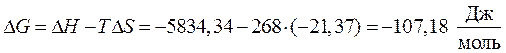Вывод. По результатам расчета видно, что при превращении 1 моль переохлажденной воды в лед энтальпия и энтропия в системе убывает. Это значит, что самопроизвольный процесс в таком случае возможен только при низких температурах, когда энергия Гиббса DG приобретает отрицательные значения (см. табл.2), что мы и наблюдаем в нашем примере.