Политропные процессы и их обобщающее значение

Политропными называют любые закономерные термодинамические процессы удовлетворяющие уравнению

pv ⁿ = const. (6.29)

Каждому политропному процессу соответствует какое-либо значение отношения

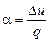. (6.30)

Изменение внутренней энергии в политропном процессе можно выразить следующим образом

du = c_v dT = a dq,

откуда количество подводимой теплоты будет равно

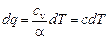, (6.31)

где с - теплоемкость газа в политропном процессе

Напишем для политропного процесса уравнение первого закона термодинамики, выраженное через параметры газа

cdT = c_v dT + pdv

или

(с - с_v)dT - pdv = 0.

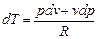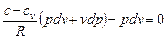Поскольку , то , или

.

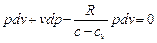Заменив в этом выражении R = c_p - c_v, получим

.

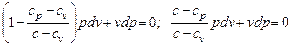Для конкретного политропного процесса коэффициент 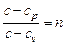, то .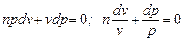

pv ⁿ = const. (6.32)

Это уравнение политропного процесса, который можно рассматривать как обобщающий процесс, так как из этого уравнения при определенных значениях показателя n можно получить все другие процессы, а также и другие возможные.

Очевидно, при n = k получим уравнение адиабатического процесса

pv ^k = const;

при n = 1 - уравнение изотермического процесса

pv = const;

при n = 0 - уравнение изобарного процесса

p = const.

Для нахождения показателя изохорного процесса извлечем корень n-ой степени из уравнения (6.32)

.

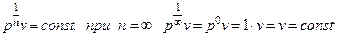Следовательно, уравнение изохорного процесса v = const можно получить при n ® .

На рис. 6.4 показано расположение политроп, построенных из одной и той же точки 1, при разных значениях показателя n, который изменяется от + до - . Для тепловых машин, кроме изохорного, изобарного, изотермического и адиабатного процессов, имеют большое значение политропные процессы, располагающиеся между изотермическим и адиабатным процессами, как предельными, т. е. с показателем n, лежащим в пределах 1< n < k.

Рис. 6.4. Политропные процессы в координатах pv

Для политропных процессов с показателем 1< n < k можно написать зависимости между параметрами, аналогичные зависимостям адиабатного процесса:

.

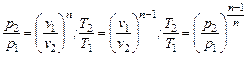Работа в политропном процессе равна

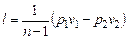. (6.33)

Изменение внутренней энергии

D u = c_v (T ₂ - T ₁). (6.34)

Количество теплоты

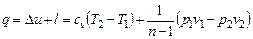. 6.35)

Теплоемкость в политропном процессе

. (6.36)

Подставляя в (6.37) соответствующие значения n для основных процессов, получим для них выражения теплоемкости с:

- изохорный процесс (n = ): c = c_v;

- изобарный процесс (n = 0): c = c_p;

- изотермический процесс (n =1): c = ;

- адиабатный процесс (n = k): c = 0.

Пример 6.1. Сосуд вместимостью 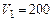л содержит кислород при абсолютном давлении 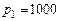кПа и температуре 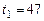°С. Определить массу газа, конечную температуру, изменение энтропии и количество теплоты, которое необходимо подвести, чтобы повысить давление в процессе при постоянном объеме до 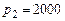кПа. Удельная теплоемкость – величина переменная.

Р е ш е н и е. Масса кислорода – по уравнению Клапейрона:

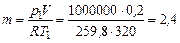кг.

Конечная температура для процесса :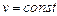

К = 367°С.

Количество теплоты, сообщенной на изменение внутренней энергии кислорода для процесса :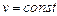

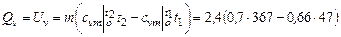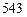= кДж.

Изменение энтропии для процесса :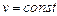

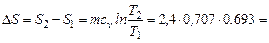1,17 кДж/К.

Пример 6.2. В цилиндре двигателя объемом 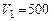л находится газ (со свойствами воздуха) при избыточном давлении =

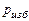= 3900 кПа и температуре 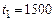°С. Атмосферное давление 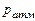= 100 кПа. От газа отнимается количество теплоты при постоянном давлении до температуры 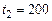°С. Определить массу газа, конечный объем, изменение внутренней энергии, количество отнятой теплоты, совершенную над газом работу сжатия и изменение энтропии.

Р е ш е н и е. Абсолютное давление :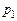

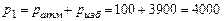кПа.

Масса газа:

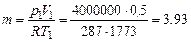кг.

Конечный объем для процесса :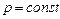

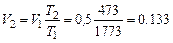м³ = 133 л.

Изменение внутренней энергии:

=

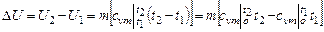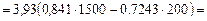- 4400 кДж.

Количество отнятой теплоты в процессе :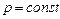

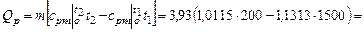
= - 5875 кДж.

Date: 2015-05-09; view: 1208; Нарушение авторских прав