Энтропия. Клазиус Рудольф Юлиус Эммануил (1818-1889) при исследовании термодинамических процессов рассматривал функцию состояния термодинамической системы вида

Клазиус Рудольф Юлиус Эммануил (1818-1889) при исследовании термодинамических процессов рассматривал функцию состояния термодинамической системы вида

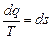, Дж/кг×К, (6.1)

которую назвал энтропия s.

Необходимость введения новой функции состояния термодинамической системы определяется прежде всего тем, что сама теплота q не является функцией состояния и dq = du + pdv не является полным дифференциалом; dq представляет собой только некоторую бесконечно малую величину. Для того чтобы проинтегрировать правую часть уравнения dq = du + pdv, должна быть известна зависимость р от v или р от Т.

Энтропия является однозначной функцией состояния тела, ее изменение не зависит от промежуточных состояний тела (от характера процесса). Изменение энтропии в идеальном цикле (состоящем из обратимых процессов) равно нулю.

Изменение энтропии идеального газа в обратимых процессах можно определить, если подставить вместо dq его значение из первого закона термодинамики, предварительно выразив изменение внутренней энергии через теплоемкость du = c_v dT. Будем иметь

.

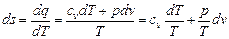Из уравнения состояния идеального газа получим 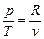, подставив которое, получим

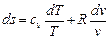. (6.2)

После интегрирования будем иметь для изменения энтропии

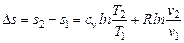. (6.3)

Для получения изменения энтропии как функции T и p нужно из уравнения (6.2) исключить v. Из уравнения Клапейрона после дифференцирования последнего получим

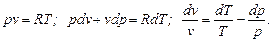
Подставляя значение dv / v в (6.2), имеем

,

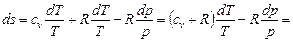
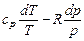так как по уравнению Майера c_p - c_v = R и с_v + R = c_p.

Интегрируя при с_р = const, находим

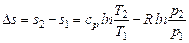. (6.4)

Для получения изменения энтропии как функции р и v следует в уравнении (6.2) исключить Т. Дифференцируя уравнение состояния, получим для Т:

,

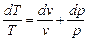подставив это выражение в (6.2), получим для изменения энтропии

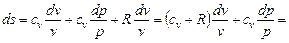
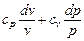
Интегрируя полученное выражение, получаем

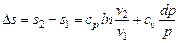. (6.5)

Так как изменение энтропии не зависит от характера процесса, полученные уравнения энтропии справедливы как для обратимых, так и для необратимых процессов.

Итак, полученные выражения для энтропии:

· при р = const: ;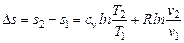

· при v = const: ;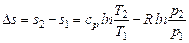

· при Т = const: .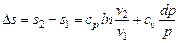

6.2. Тепловая Тs - диаграмма

Энтропию можно применять совместно с одним из основных параметров для графического изображения процессов. Удобнее всего энтропию сочетать с абсолютной температурой. Если энтропию s откладывать по оси абсцисс, а абсолютную температуру - по оси ординат, то получим координатную систему Тs, т. е. Ts - диаграмму, где состояние газа графически изображается точкой, а процесс в виде кривой, уравнение которой можно представить как Т = f (s). Элементарная теплота процесса dq = Tds изображается на диаграмме элементарной площадкой, высота которой равна Т, а основание ds, рис. 6.1.

Рис. 6.1. Ts – диаграмма

Площадь под кривой процесса 1-3-2 изображает в некотором масштабе теплоту, подводимую в этом процессе

q _1-2 = пл. 5-1-3-2-6-5 = .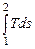

Если в процессе энтропия увеличивается, то это означает, что тепло подводится к телу и, наоборот, если энтропия уменьшается, то тепло отводится. Это означает, что энтропия и теплота имеют одинаковые знаки.

Обратимый круговой процесс на Ts - диаграмме изображается площадью фигуры 1-3-2-4-1.

Разность между подведенной и отведенной теплотой, согласно первому закону термодинамики, представляет собой полезную внешнюю работу, которую совершает 1 кг рабочего тела при круговом обратимом процессе над внешней системой:

.

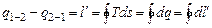Таким образом, на Ts -диаграмме удельная работа тела (1 кг) при обратимом круговом процессе численно равна площади внутри замкнутой линии и дает наглядное представление об изменении температуры рабочего тела.

Общие вопросы исследования процессов

Первый закон термодинамики устанавливает взаимосвязь между количеством теплоты, изменением внутренней энергии и внешней работы газа. Причем количество теплоты, подводимое к телу или отводимое от него, зависит от характера процесса.

Основные процессы:

· изохорный, протекающий при постоянном объеме;

· изобарный, протекающий при постоянном давлении;

· изотермный, протекающий при постоянной температуре;

· адиабатный, протекающий при отсутствии теплообмена с внешней средой.

Кроме того, существует группа процессов, являющихся при определенных условиях обобщающими для основных процессов. Эти процессы называются политропными и характеризуются постоянством теплоемкости в процессе.

Для всех процессов принят общий метод исследований, который заключается в следующем:

· выводится уравнение кривой процесса на pv - и Ts -диаграммах;

· устанавливается зависимость между основными параметрами рабочего тела в начале и конце процесса;

· определяется изменение внутренней энергии по формуле, справедливой для всех процессов идеального газа:

,

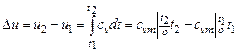или при постоянной теплоемкости: ;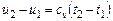

· вычисляется работа изменения объема газа по основной формуле: ;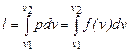

· определяется количество теплоты, участвующее в процессе, по формуле:

;

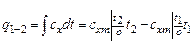· определяется изменение энтальпии в процессе по формуле, справедливой для всех процессов идеального газа:

;

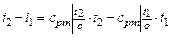или для постоянной теплоемкости:

;

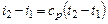· определяется изменение энтропии идеального газа по формулам:

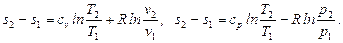
Рассматриваемые процессы считаются обратимыми.

Date: 2015-05-09; view: 1172; Нарушение авторских прав