Теплоемкость при постоянном объеме и давлении

Как и другие параметры термодинамической системы теплоемкость зависит от характера процесса. Различают теплоемкость при постоянном объеме

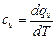, (5.3)

равную отношению количества теплоты dq_v в процессе при постоянном объеме к изменению температуры dT тела, и теплоемкость при постоянном давлении

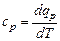, (5.4)

равную отношению количества теплоты 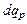в процессе при постоянном давлении к изменению температуры dT тела.

В равновесном процессе нагревания тела элементарное количество теплоты, в соответствии с первым законом термодинамики будет

dq = du + dl = du + pdv.

Изменение внутренней энергии du есть полный дифференциал функции состояния, т. е.

,

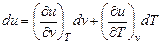подставив который в формулу для первого закона термодинамики, получим

. (5.5)

Для процесса v = const изменение dv = 0, тогда (5.5) принимает вид

.

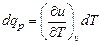Тогда, подставив вместо dq_v его выражение из (5.3), получим для теплоемкости при v = const следующее выражение

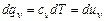и . (5.6)

При v =сonst, когда тело не совершает внешней работы, вся теплота, сообщаемая телу, идет на изменение его внутренней энергии, или при c_v = const для изменения теплоты в процессе будем иметь

q _{1- 2,v} = u ₂ - u ₁ = c_v (t ₂ - t ₁). (5.7)

Изменение внутренней энергии идеального газа равно произведению теплоемкости c_v при постоянном объеме на разность температур.

Интегрируя уравнение (5.6) для идеального газа от 0°С до t, получим: .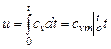

Отсюда для любого конечного процесса изменения состояния идеального газа имеем

.

Подставим значение du = c_vdT в основное уравнение первого закона термодинамики, имеем в общем случае для обратимого процесса при бесконечно малом изменении состояния идеального газа

dq = c_v dT + pdv. (5.8)

Для процесса p = const, когда переменными являются Т и v из уравнения первого закона термодинамики получим

.

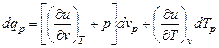Поскольку dq_p = c_p dT, то

.

Но , тогда будем иметь для теплоемкости при постоянном давлении

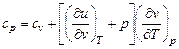. (5.9)

Уравнение (5.9) в общем виде устанавливает связь между теплоемкостями с_v и с_p.

Для идеального газ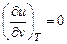а , а 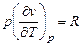, (что следует из уравнения состояния pv = RT), тогда (5.9) запишется в виде

c_p = c_v + R и c_p - c_v = R.

Это уравнение носит название уравнение Майера.

Оно может быть записано и для кмоль газа:

m С_p - m С_v = 8314,3 Дж/кмоль×град.

Следовательно, для идеальных газов разность между теплоемкостями с_р и с_v есть величина постоянная.

Для реальных газов с_р - с_v > R, так как при расширении реальных газов (при р = const) совершается не только внешняя, но и внутренняя работа, связанная с изменением потенциальной энергии тела, что и вызывает больший расход теплоты.

Date: 2015-05-09; view: 1268; Нарушение авторских прав