Внутренняя энергия

Любая термодинамическая система обладает определенным запасом энергии, некоторая доля которого зависит только от внутреннего состояния системы. Другая часть полного запаса энергии системы может определяться взаимодействием рабочего тела системы с внешней средой (потенциальная энергия), либо представлять собой кинетическую энергию движения системы относительно окружающей среды. Так, для земного наблюдателя полная энергия газа, хранящегося в баллоне летящего космического корабля, значительно больше энергии газа в баллоне корабля, стоящего на стартовой площадке, за счет подъема на значительную высоту и разгона до заданной скорости. При этом термодинамическое состояние самого газа, определяемое значениями его давления и температуры, может быть одинаковым.

Та часть запаса энергии термодинамической системы, которая не связана с положением системы в поле внешних сил и с движением самой системы относительно окружающей среды, называется внутренней энергией системы.

Кинетическая и потенциальная энергии системы должны вводиться в термодинамические соотношения в виде самостоятельных выражений дополнительно к внутренней энергии термодинамической системы. Внутренняя энергия системы является функцией ее состояния и может быть вычислена с помощью уравнения состояния. Ее значение не зависит от того, каким образом (по какому пути) система достигла данного состояния.

Внутренняя энергия тела есть вся энергия, заключенная в теле. Она также может быть представлена в виде суммы отдельных видов энергий: кинетической энергии молекул, включающей энергию поступательного и вращательного движения молекул, а также колебательного движения атомов в самой молекуле; энергии электронов; внутриядерной энергии; энергии взаимодействия между ядром молекул и электронами; потенциальной энергии или энергии положения молекул и т.д. нутренняя энергия системы выражается следующей формулой

,

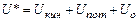где 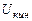- внутренняя кинетическая энергия молекул; 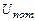- внутренняя потенциальная энергия молекул; 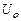- постоянная интегрирования.

Внутреннюю кинетическую энергию можно разделить на следующие составляющие

где 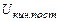- кинетическая энергия поступательного движения молекул, 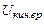_.- то же, вращательного движения молекул, 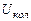- энергия колебательного движения ядер атомов молекулы относительно друг друга.

Величина U ₀ представляет собой нулевую энергию или внутреннюю энергию при температуре абсолютного нуля. При температуре Т = 0 тепловое движение молекул и атомов, входящих в молекулы прекращается, но движение частиц внутри атомов продолжается. Например, движение электронов в атомах не является тепловым движением и имеет место при любых температурах, в том числе и при Т = 0. В термодинамике рассматриваются не абсолютные значения внутренней энергии, а ее изменения в результате происходящих процессов, поэтому для большинства технических задач значение U ₀ не требуется, и ее обычно полагают равной нулю.

В технической термодинамике рассматриваются только такие процессы, в которых изменяются кинетическая и потенциальная энергии. Поэтому под внутренней энергией для идеальных газов понимается кинетическая энергия движения молекул и энергия колебательного движения атомов в молекуле, а для реальных газов еще дополнительно и потенциальную составляющую энергии, связанную с наличием сил взаимодействия между молекулами и зависящую от расстояния между ними.

Отсчет внутренней энергии может производиться от любого условного нуля. Так, например для идеальных газов принято считать внутреннюю энергию при t = 0°С равной нулю. оскольку кинетическая составляющая внутренней энергии определяется температурой тела, потенциальная ее составляющая зависит от расстояния между молекулами (удельного объема), то полная внутренняя энергия является функцией двух параметров и в данном конкретном состоянии тела будет иметь вполне определенную величину. Такие величины, как было уже сказано, называются параметрами состояния. Следовательно, внутренняя энергия, являясь параметром состояния, представляет собой одновременно однозначную непрерывную и конечную функцию состояния системы. нутренняя энергия сложной системы, отнесенная к 1 кг, равна сумме внутренних энергий ее отдельных составляющих, т.е.

.

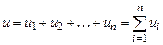Из закона сохранения энергии следует, что термодинамическая система в каждом своем состоянии может иметь только одно значение. Следовательно, в термодинамической системе изменение внутренней энергии газа не зависит от характера или пути по которому происходили эти изменения, а будет определяться заданным начальным и конечным состояниями:

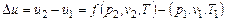. (4.1)

Это наглядно иллюстрируется на изотермах состояния системы, рис. 4.1. Каждому изменению соответствуют определенные значения удельного объема и давления при различных значениях температуры, но начальное и конечное состояние остается неизменным. Поэтому во всех этих процессах изменение внутренней энергии системы будет одно и то же, т.е.

.

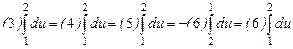В круговых процессах изменение внутренней энергии равно нулю: .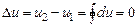

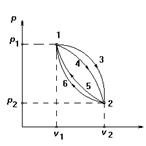
Рис. 4.1. Иллюстрация изменения внутренней энергии

термодинамической системы

Приращение du, как и любого параметра является полным дифференциалом. Поскольку состояние газа вполне определяется основными параметрами состояния, внутреннюю энергию можно представить как функцию любых двух параметров состояния:

u = f (T, v); u = f (T, p); u = f (p, v),

или полные дифференциалы внутренней энергии:

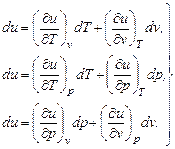(4.2)

Внутренняя энергия идеального газа не зависит от объема или давления, так как в нем отсутствуют силы взаимодействия между молекулами, поэтому

.

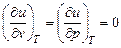Внутренняя энергия идеального газа зависит только от температуры u = f (T), следовательно, производная от внутренней энергии идеального газа по температуре есть полная производная:

.

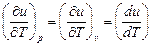В таком случае, можно записать

.

Изменение внутренней энергии идеального газа зависит только от начальной и конечной температуры процесса.

Далее рассмотрим другие закономерности изменения внутренней энергии термодинамической системы в частности работу.

Работа

Передачу энергии от одного тела к другому, связанную с изменением объема рабочего тела, с перемещением его в пространстве или с изменением его положения, называют работой. В производстве работы всегда участвуют два или больше тел. Первое тело, производящее работу, отдает энергию. Работа является макроскопической формой передачи энергии от одного тела к другому.

Совершаемая газом работа при его расширении зависит от изменения параметров состояния p, v, T.

Для вывода уравнения работы газа при его расширении рассмотрим частный случай - получение работы в равновесном процессе при постоянном давлении, рис. 4.2.

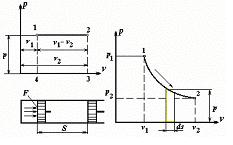
Рис. 4.2. Процесс расширения газа при постоянном давлении

В цилиндре под поршнем находится газ при давлении p, равном в равновесном процессе давлению среды, и удельном объеме v ₁; площадь поршня F. Если сообщить газу некоторое количество теплоты, то он будет расширяться при постоянном давлении и перемещать поршень до положения в точке 2.

Сила, действующая на поршень, равна pF, путь перемещения поршня равен S. Работа, совершаемая газом при перемещении поршня, равна

l = pFS,

но произведение FS есть разность удельных объемов v ₁- v ₂, поэтому

l = p ×(v ₂ - v ₁) = p ×D v. (4.3)

Элементарная работа dl, совершаемая системой в равновесном процессе изменения состояния газа, при бесконечно малом изменении объема, определится по формуле

dl = pdv. (4.4)

Полная работа l, совершаемая системой при бесконечно малом изменении объема в произвольном равновесном процессе, изображается кривой 1 - 2 и равна

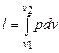. (4.5)

Зная функциональную зависимость параметров p и v в процессе или уравнение вида p = f (v), можно аналитически определить работу для любого равновесного процесса в указанных пределах.

Если система совершает работу во внешней среде, где давление 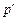, то работа расширения системы при увеличении объема на dv равна 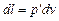, а при конечном изменении объемов от v ₁ до v ₂

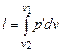. (4.6)

В равновесном процессе 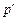= p.

Если расширение системы происходит в пустоту, когда давление 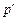на границах системы и внешней среды равно нулю и никаких перемещений внешних тел не наблюдается, работа равна нулю, что и вытекает из формулы (4.6).

Date: 2015-05-09; view: 1409; Нарушение авторских прав