Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
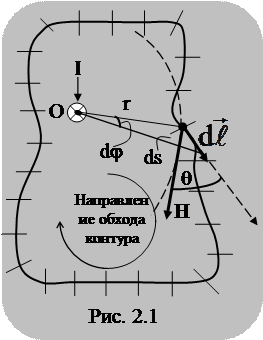
Циркуляцией вектора напряженности магнитного поля по замкнутому контуру L (или просто циркуляцией вектора напряженности магнитного поля) называют интеграл
|
|
.
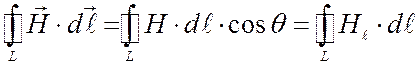Окружность:
.
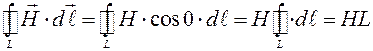С учетом того что напряженность магнитного поля от бесконечно длинного проводника с током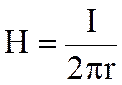 
, а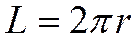 
, имеем
.
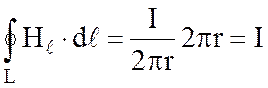Таким образом,
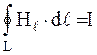. (2.2)
Если внутри замкнутого контура находятся n токов, то
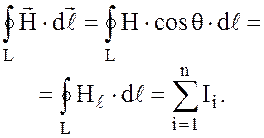(2.3)
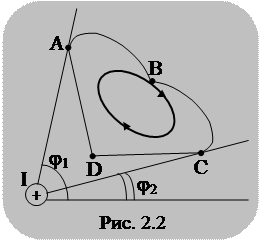
Если ток протекает вне контура (рис. 2.2), то в этом случае можно записать
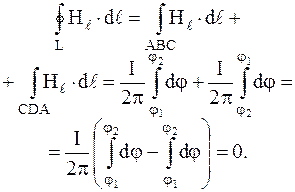(2.4)
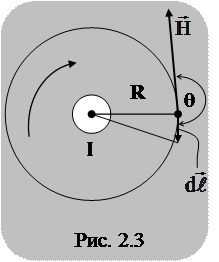
Соотношение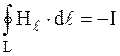 
справедливо и в том случае, когда контур и проводник имеют произвольную форму. Если ток направлен «на нас», то вектор 
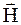направлен «против часовой стрелки» (рис. 2.3). В этом случае 
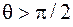и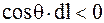 
. В результате получим
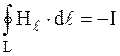. (2.5)
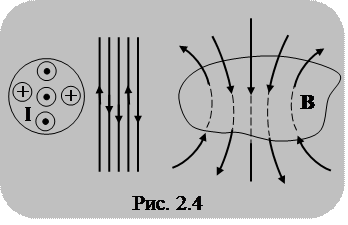Если же контур охватывает 
проводников с токами, направленными в разные стороны, то, учитывая, что от положения проводника внутри контура не зависит циркуляция , можем мысленно собрать все проводники в «жгут», толщина которого в силу конечности мала. По «жгуту» протекает ток, равный алгебраической сумме токов отдельных проводников (рис. 2.4).
Утверждение (2.3), что циркуляция вектора напряженности магнитного поля по замкнутому контуру L равна алгебраической сумме токов, охватываемых контуром, называется теоремой о циркуляциимагнитного поля или законом полного тока в интегральной форме. Таким образом, из закона полного тока вытекают следующие следствия:
а) если направление обхода контура и направление тока в проводнике не связаны между собой правилом правого винта, то значение
,
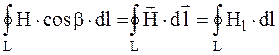сохранив величину, изменит знак;
б) если контур, расположенный в магнитном поле, не охватывает ток или алгебраическая сумма токов внутри замкнутого контура равна нулю, то
.
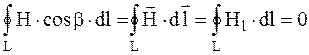Зная связь между векторомнапряженности H и вектором индукции B магнитного поля, можно записать закон полного тока в интегральной форме для циркуляции вектора индукции:
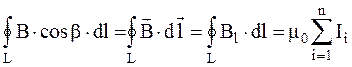. (2.6)
Так как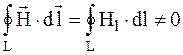 
, 
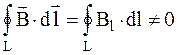, то магнитному полю нельзя приписать какой-либо потенциал, а это означает, что магнитное поле является вихревым, а не потенциальным.
2.2. Применение закона полного тока для расчета магнитных полей
2.2.1. Напряженность поля бесконечно длинного соленоида
Соленоидом называют катушку цилиндрической формы из провода, витки которой намотаны в одном направлении и прилегают плотно друг к другу.
Магнитное поле соленоида представляет собой результат сложения полей, создаваемых несколькими круговыми токами, расположенными рядом и имеющими общую ось (рис. 2.6).
Внутри соленоида силовые линии каждого отдельного витка имеют одинаковое направление. Поэтому принято считать поле бесконечно длинного соленоида (такого, у которого диаметр гораздо меньше длины – d<<L) однородным, существующим только внутри его.
 |
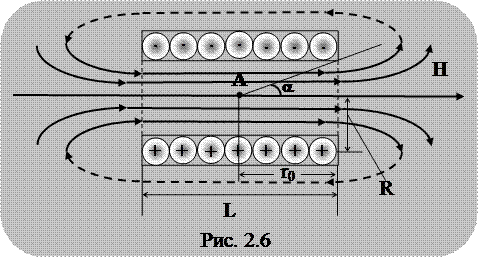Рассчитаем напряженность магнитного поля внутри соленоида, длина которого L, радиус витка R, число витков N, сила тока I. Будем считать, что в любой точке соленоида вектор H направлен параллельно оси.
Для расчета напряженности воспользуемся законом полного тока в виде
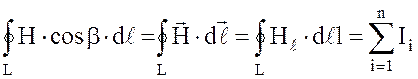. (2.7)
 |
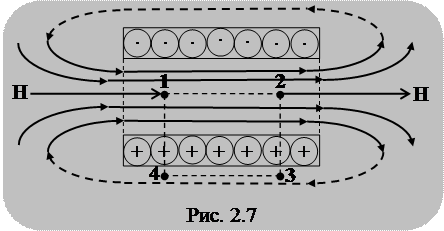Выберем замкнутый контур прямоугольной формы (рис. 2.7), участок 1-2 которого расположен внутри соленоида вдоль его оси.
Левую часть выражения (2.7) можно представить в виде
,
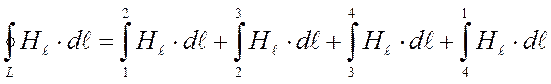где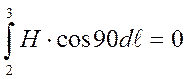 
, так как H перпендикулярен участку 2-3;
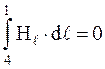, так как H перпендикулярен участку 4-1;
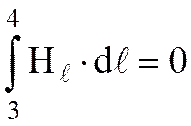, так как участок 3-4 находится вне соленоида.
Следовательно,
.
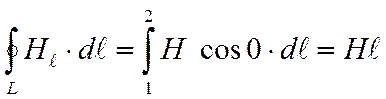Правая часть выражения (2.16) может быть представлена так:
,
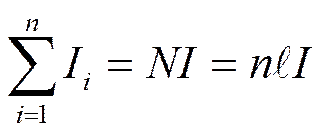где n - число витков на единице длины соленоида;
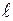- длина участка;
I - величина тока в соленоиде.
Таким образом, имеем
.
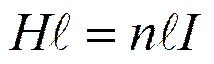Откуда
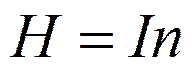. (2.8)
Формула (2.8) согласуется с формулой, полученной с применением закона Био-Савара-Лапласа.
Из полученного результата действительно видно, что напряженность магнитного поля внутри бесконечно длинного соленоида имеет одно и тоже значение, а следовательно, оно действительно однородно.
Таким образом, действительно внутри бесконечно длинного соленоида напряженность магнитного поля практически везде одинакова. Она направлена вдоль оси соленоида в соответствии с правилом правого винта.
Date: 2015-05-09; view: 1417; Нарушение авторских прав