Тест 10

ВОЛНЫ

Основные типы волн, которые наблюдаются в природе: упругие и

электромагнитные.

В зависимости от направления колебаний частиц по отношению к направлению распространения волны различают: продольные и поперечные волны.

В продольной волне частицы среды колеблются вдоль направления распространения волны. Продольные волны возникают в таких средах, где возникают деформации сжатия/растяжения (т.е. в газах, жидкостях и твердых телах).

В поперечной волне – частицы среды колеблются в направлениях перпендикулярных к направлению распространения. Поперечные волны возникают в средах, где присутствуют деформации сдвига (только в твердых телах).

Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.

Бегущими волнами называются волны, которые переносят в пространстве энергию. График волны – это зависимость смещения всех частиц среды от расстояния до

источника колебаний в данный момент t.

Геометрическоеместоточек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом).

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.

Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент t только один. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической.

Сферические волны испускаются точечными источниками, плоские волны – протяженными источниками. Достаточно далеко от источника сферическую волну можно рассматривать как плоскую.

Расстояниеl,накотороераспространяетсяволназавремя,равноепериодуколебания

частиц среды, называется длиной волны:

колебаний – определяется числом колебаний за 2 p секунд.

Длинуволны l можноопределитьтакжекакрасстояниемеждуближайшимиточкамисреды, колеблющихся с разностью фаз, равной 2 p.

Уравнением волны называется выражение, которое дает смещение колеблющейся частицыкакфункцию ее координат x, y, z и времени t: =x (x,y,z,t).

Дифференциальное волновое уравнение:

∆x =

1 ¶ 2 x

V2 ¶ t2

 

(1.2)

 

¶ ¶ ¶

222

где ∆ = ¶ x2 + ¶ y2 + ¶ z2 – оператор Лапласа.

 

 

	=
		.
	=
		.

Дифференциальное волновое уравнение сферической незатухающей волны, распространяющейся в произвольном направлении:

¶ 2 x 1 ¶ 2 x ¶ r2V2 ¶ t2

 

Дифференциальное волновое уравнение распространяющейся в направлении оси Х:

 

(1.3)

 

плоской незатухающей волны,

 

¶ 21 ¶ 2 x ¶ x2V2 ¶ t2

 

Решение уравнения (1.3) – есть уравнение бегущей сферической волны:

 

(1.4)

 

r

x (r,t) = acos (w t − kr +f 0), (1.5)

 

где r – расстояние от источника волны до рассматриваемой точки среды; j0 – начальная фаза колебаний; a – множитель, определяющий амплитуду волны в точке среды, находящейся на

 

r

r

расстоянииотисточникаволны r=1 м. Амплитуда колебаний волны убывает с расстоянием от источника по закону 1/r.

Волновойвектор k = k × n –вектор,направленныйвсторонураспространенияволныи

 

w

имеющий длину:

k = k = V = 2 p, (1.6)где n – нормаль к волновой поверхности.

Решение уравнения (1.4) – есть уравнение бегущей плоской волны,

распространяющейся вдоль оси x:

x (x,t) =x 0cos (w t − kx +f 0), (1.7)гдеx (x,t) –смещениеколеблющейсячастицыупругойсреды; 0 –амплитудаволны(максимально возможное смещение частицы); x – расстояние от источника колебаний до точки, для которой определяется смещение.

 

Фазовая скорость – скорость перемещения отдельной волны в некотором направлении:

 

dx

r

V = dt. (1.8) Волны, как правило, перемещаются группой (пакетом), поэтому можно ввести

групповуюскорость u – это скорость перемещения энергии группы волн.

d

u = V −l dV. (1.9)

 

Среднее по времени значение плотности энергии переносимой волной в каждой точке среды равно:

 

< w >= 2 rw 2 x 02, (1.10) гдеr – плотность сплошной среды.

 

Плотность потока энергии, переносимой волной, равна:

 

j = wV = 2 rw 2 x 0V. (1.11) Если среда, в которой распространяется одновременно несколько волн, линейна, т. е. ее

свойства не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения) волн: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.

 

 

		,
		.

Электромагнитная волна – это переменное электромагнитное поле, распространяющееся в пространстве с конечной V.

Для однородной и изотропной среды вдали от зарядов и токов, создающих

 

r

r

ì

электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей E и H переменного электромагнитного поля удовлетворяют системе волновых уравнений:

ï

22

¶

Vt

ï∆ E = 1 ¶ 2E

í

r

r

¶

∆ =

H

ï

. (1.12) ï 1H

 

î V2 ¶ t2

 

Фазовая скорость электромагнитных волн определяется выражением:

 

 

n

V=c =

e 0 µ 0 eµ

 

(1.13)

 

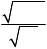где e 0, µ 0 – электрическая и магнитная постоянные; e, µ – диэлектрическая и магнитная проницаемости среды; n – абсолютный показатель преломления среды; с = 3 × 108 м/с – скорость света в вакууме.

r r

Следствием теории Максвелла является поперечностъ электромагнитных волн:

 

r

E ^ H ^ V. На рисунке 1 показана мгновенная «фотография» плоской электромагнитной

 

волны. Векторы E, H, V – образуют правовинтовую систему и колеблются в одинаковых фазах, т.е. одновременно достигают максимальных и нулевых значений.

 

 

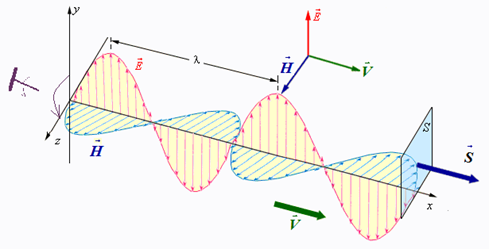Рис. 1

 

 

Решение системы уравнений (1.12) – есть система уравнений монохроматической бегущей электромагнитной волны:

ì Ey = E0ycos (w t − kx +f 0)

 

ï

î Hz = H0zcos (w t − kx +f 0)

плоской

 

(1.14)

 

Объемная плотность энергии электромагнитной волны:

 

H

E

0 0

w em =w e +w m =ee2 2+µµ2 2=ee0µµ0 EH, (1.15)где w e, w m −объемные плотности энергии электрического и магнитного полей.

 

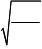
Вектор плотности потока энергии (Умова – Пойнтинга) S – направлен в сторону распространения электромагнитной волны, его модуль равен энергии, переносимой электромагнитной волной за 1 времени через единичную площадку, перпендикулярную направлению распространения волны:

 

	E		.

r

r

ë û

S = é E,H ù. (1.16)

 

Модуль плотности потока энергии:

 

m

S = eV = EH. (1.17) Интенсивность электромагнитной волны I – это величина численно равная энергии, которую переносит волна за 1 времени сквозь 1 площади поверхности, перпендикулярную направлению распространения волны. Для плоской

монохроматической волны:

 

 

22

I = 1EH = 1

ee o2 µµ o

 

(1.18)

 

Решение тестовых задач раздела «Волны»

Тест 1

Скорость звука в воздухе равна 330 м/с. При частоте 50 Гц длина волны равна …

 

А) 6,6 км Б) 16500 м В) 0,15 м Г) 6,6 м

 

Решение:

 

v

Найдем длину волны из формулы (1.1): l V. Выполним расчет: l = 330 = 6,6 м.

 

Ответ: Г.

 

Тест 2

H

E

На рисунке 2 показана ориентацияrвекторовнапряженности электрического и магнитного полей в электромагнитной волне. Вектор плотности потока энергии электромагнитного поля (вектор Умова – Пойнтинга) ориентирован в направлении …

А) 1 Б) 2 В) 3 Г) 4

 

r

r

Решение:

 

Вектора E ^ H ^ S образуют правовинтовую

r r

систему. Воспользуемся правилом правого винта: винт Рис.2 устанавливаем перпендикулярно плоскости векторов E и

r

H так чтобы был поворот от E к H по наименьшему углу. Острие винта укажет

 

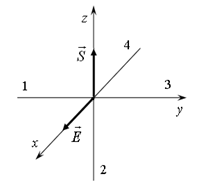направление вектора S. Ответ: А.

 

Тест 3

На рисунке 3 показана ориентация вектора

 

r

напряженности электрического поля E в электромагнитной

 

r

волне и вектора плотности потока энергии электромагнитного поля (вектора Умова – Пойнтинга).

 

Вектор напряженности магнитного поля H в электромагнитной волне ориентирован в направлении …

А) 1 Б) 2 В) 3 Г) 4

r

r

Решение: Рис.3

 

r

r

Вектора E ^ H ^ S образуют правовинтовую систему. Воспользуемся правилом правого винта для определения направления H: острие винта указывает направление

вектора S, а поворот от E к H происходит по наименьшему углу. Ответ: В.

 

 

		A
	A
		A

Тест 4

w

Плоскаязвуковаяволнаx(x,t)= Acos (w t − kx) распространяетсявупругойсреде.Скоростьколебаниячастицсреды,отстоящихотисточниканарасстоянии x =l 6,поистечениивремени t = T4 посленачалаколебаний источника равна …

 

А)− A Б)

w

 

2

В)− A Г) w Д)− w 3

 

Решение:

(

Скорость колебания частиц среды, отстоящих от источника, равна:

p

x

T

w

w

w

ç ÷ ç ÷

l

623

è ø è ø

Vx = d x dt,t)=− A × sin (w t − kx)==− A × sin æ T4 − 2 plö=− A × sin æp−pö=

 

w

A

w

= − A × sin6 = − 2. Ответ: А.

 

Тест 5

Вупругойсредеплотностью r распространяется плоская синусоидальная волна. Если амплитудаволны увеличится в 4 раза, то плотность потока энергии …

А)увеличитсяв 16 раз Б) увеличится в 4 раза В) уменьшится в 16 раз Г) уменьшится в 4 раза Д) не изменится

Решение:

x

V

Плотность потока энергии переносимой волной запишем согласно (1.11): j = 1 rw 2 x 02, Þ j02. Если амплитуда волны увеличится в 4 раза, то плотность потока

 

энергии возрастет в 16 раз. Ответ: А.

 

Тест 6

p

æ ö æ ö

м м

è ø è ø

Если в электромагнитной волне, распространяющейся в вакууме вдоль оси ОХ, компоненты векторов напряженностей электрического и магнитного полей изменяются по закону Ey = 750sin çw t − 2x + 2 ÷ В, Hz = 2sin çw t − 2x + 2 ÷A, то круговая частота

 

равна…

 

32

А) 3 × 108c − 1 Б) 2 × 10 − 8c − 1 В) 3 × 10 − 8c − 1 Г) 6 × 10 − 8c − 1 Д) 6 × 108c − 1

Решение:

Воспользуемсяоднимизуравненийсистемы(1.14): Ey = E0ycos (w t − kx +f 0),Þ k = 2. Из (1.6) найдем: w = kV = kc. Выполним расчет: w = 2 × 3 × 108 = 6 × 108c − 1.

 

Ответ: Д.

 

Тест 7

ç ÷

24

è ø

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет видx= 0,01sin æp t −p x ö,м.Фазаколебанийточки,расположеннойнарасстоянии 2 мот

 

источника колебаний, в момент времени 2 с равна …

А) /4 Б) p /2 В) p Г) p Д) /8

 

Решение:

Фаза колебаний точки в уравнении плоской волны представлена величиной стоящей в

 

 

ç ÷

24

è ø

p p

ç ÷

è ø

скобках: f = æp t − p x ö.Выполним расчет: f æ 22 − 42 ö= 2. Ответ: Б.

 

Тест 8

При уменьшении в 2 раза амплитуды колебаний электрического и магнитного полей плотность потока энергии …

А)уменьшитсяв 4 раза Б) увеличится в 2 раза Г)увеличится в 4 раза Д) не изменится

 

 

векторов напряженности

 

 

В) уменьшится в 2 раза

 

Решение:

Плотность потока энергии переносимой электромагнитной волной определим из (1.17): S1 = E1H1. Послеуменьшенияамплитудколебаний: S2 = E1H1.

 

EH

211

Найдем отношение: S1 = 4E1H1 = 4. Ответ: А.

 

Тест 9

Рис.4

На рисунке 4 представлена мгновенная «фотография» электрической составляющей электромагнитной волны, переходящейизсреды 1 в среду 2, перпендикулярно границе раздела АВ. Уравнения, описывающие электрические

() ()

напряженности волны в каждой среде в скалярной форме имеют вид:

 

E1 = E0sin w t − 5 × 106 p × x и E2 = E0sin w t − 8 × 106 p × x. Относительный показатель

 

преломления среды 2 относительно среды 1 равен …

А) 1,6 Б) 1,5 В )0,625 Г) 2 Д) 1,3

 

Решение:

n

n

Относительныйпоказательпреломлениясреды 2 относительносреды 1: 21 = n –(1), 1

 

nn

V

VV

k

w

гдеабсолютныепоказателипреломления 1 = c и 2 = c. Из(1.6)имеем: 1 = w, 121

 

n

Vk

V = k2. Из уравнений, описывающих электрические напряженности волны в каждой среде: k1 = 5 × 106, k2 = 8 × 106 p.Выполним подстановку формул в выражение (1): 21 = V = k2.

21

 

p

8 × 10

6 Сделаемрасчет: n1 = 5 × 106 p = 1,6. Ответ: А.

 

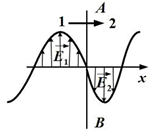
Тест 10

На рисунке 5 представлена мгновенная «фотография» электрической составляющей электромагнитной волны, переходящей из среды 1 в среду 2 перпендикулярно границе раздела АВ. Отношение скорости света в среде 1 кего скорости в среде 2 равно…

А) 1,5 Б) 0,67 В )1,6

 

Рис. 5

 

Г) 1,75 Д) 1

 

Решение:

 

Из рисунка 5 имеем: в среде 1 волна прошла расстояние x10,375 мкм, в среде 2:

 

 

 

Vx

0,375

22

x2 = 0,25 мкм.Отношение скоростей: V1 = x1 = 0,25 = 1,5.

 

Ответ: А.

Тесты для самостоятельного решения по разделу «Волны»

⇐ Предыдущая12345678910Следующая ⇒

Date: 2015-05-09; view: 1050; Нарушение авторских прав

Понравилась страница? Лайкни для друзей: