Вывод уравнения состояния. Закон Дальтона. Закон Авогадро

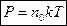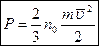, - основное уравнение молекулярно-кинетической теории идеального газа.

Отсюда можно получить уравнение состояния идеального газа:

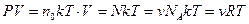Þ 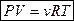- уравнение состояния идеального газа.

Если имеется смесь газов, то 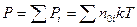- закон Дальтона (Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений)

Закон Авогадро: В равных объемах газов (V) при одинаковых условиях (температуре Т и давлении Р) содержится одинаковое число молекул.

Первое следствие из закона Авогадро: один моль любого газа при одинаковых условиях занимает одинаковый объём.

В частности, при нормальных условиях, т.е. при 0° С (273К) и 101,3 кПа, объём 1 моля газа, равен 22,4 л/моль. Этот объём называют молярным объёмом газа Vm. Пересчитать эту величину на другие температуру и давление можно с помощью уравнения Менделеева-Клапейрона:

.

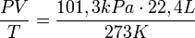
Второе следствие из закона Авогадро: молярная масса первого газа равна произведению молярной массы второго газа на относительную плотность первого газа по второму.

Используя распределение молекул по высоте Ж.Перрен экспериментально определил постоянную Авогадро. Он исследовал под микроскопом распределение броуновских частиц, т.е. считал под микроскопом число таких частиц на разных высотах в сосуде. Частицы были помещены в жидкость, плотность которой лишь на немного меньше плотности материала частиц, для того чтобы тяжелые частицы не «осели на дно», а распределились в достаточно большом слое по высоте.

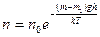, где 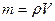- масса частицы, 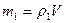- масса вытесненной воды.

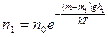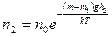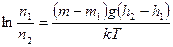, Þ Þ

.

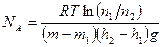71.72.(не разделены!)Распределение Больцмана.

(72)Барометрическая формула.

При выводе основного уравнения молекулярно-кинетической теории газов и макcсвелловского распределения молекул по скоростям предполагалось, что на молеку­лы газа внешние силы не действуют, по­этому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготе­ния Земли. Тяготение, с одной стороны, и тепловое движение молекул — с другой, приводят к некоторому стационарному со­стоянию газа, при котором давление газа с высотой убывает.

Выведем закон изменения давления с высотой, предполагая, что поле тяготе­ния однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте А равно р (рис. 67), то на высоте h + dh оно равно p+dp (при dh>0 dp<0, так как давле­ние с высотой убывает). Разность давле­ний р и p + dp равна весу газа, заклю­ченного в объеме цилиндра высотой Ah с основанием площадью, равной единице площади:

р- (p +d p)=r gh,

где r — плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом пределе плотность газа можно счи­тать постоянной). Следовательно,

dр=-rgdh. (45.1)

Воспользовавшись уравнением состоя­ния идеального газа pV = (m/M)RT (т — масса газа, М —молярная масса газа),находим, что

Подставив это выражение в (45.1), получим

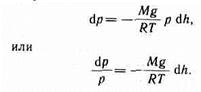
С изменением высоты от h ₁ до h ₂. дав­ление изменяется от р ₁ до p ₂ (рис. 67), т. е.

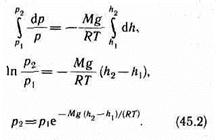
Выражение (45.2) называется барометри­ческой формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти вы­соту. Так как высоты обозначаются отно­сительно уровня моря, где давление счита­ется нормальным, то выражение (45.2) может быть записано в виде

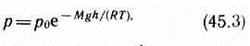
где р — давление на высоте h.

Прибор для определения высоты над земной поверхностью называется высото­мером (или альтиметром). Его работа ос­нована на использовании формулы (45.3). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяже­лее газ.

Барометрическую формулу (45.3) можно преобразовать, если воспользо­ваться выражением (42.6) p=nkT:

где n — концентрация молекул на высо­те h, n ₀ — то же на высоте h=0. Так как M = m ₀ N _A (N_A — постоянная Авогадро, m ₀ — масса одной молекулы), а R=kN_A, то

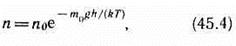где m₀gh=П — потенциальная энергия молекулы в поле тяготения, т. е.

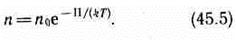
Выражение (45.5) называется распре­делением Больцмана во внешнем потенци­альном поле. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Если частицы имеют одинаковую мас­су и находятся в состоянии хаотического теплового движения, то распределение Больцмана (45.5) справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

Date: 2015-05-09; view: 3484; Нарушение авторских прав