Фундаментальная система уравнений для полу­проводников

Любой полупроводниковый прибор может находиться в одном из трех основных физических состояниях состояний:

- теплового (аналогия – озеро)

В каждой точке объема полупроводника и в любой момент времени идут уравновешивающие друг друга процессы генерации и рекомбинации носителей, но токи не текут. Все производные по пространственным переменным и по времени в модельных уравнениях равны нулю;

- стационарном (аналогия – равнинная река)

В каждой точке объема полупроводника идут неуравновешенные процессы генерации и рекомбинации, токи текут, но их величины не меняются во времени, а только от точки к точке. Все производные по времени в модельных уравнениях равны нулю;

- нестационарном (аналогия – горная река)

В каждой точке объема полупроводника идут неуравновешенные процессы генерации и рекомбинации. Токи текут и меняются во времени и от точки к точке. В модельных уравнениях присутствуют все производные по пространству и времени.

Система уравнений в частных производных, описывающих поведение полупроводникового прибора для всех трех состояний, называется фундаментальной системой уравнений (ФСУ).

Конструктивно эта система состоит из трех групп уравнений:

- уравнения для плотностей токов;

- уравнения непрерывности (переноса) для электронов и дырок (закон сохранения массы);

- уравнения Пуассона.

Фундаментальная роль этих уравнений в физике работы полупроводникового прибора аналогична роли системы уравнений Максвелла для теории электромагнитных волн.

Уравнения, описывающие плотности токов

Для одномерного случая (все величины – скалярные):

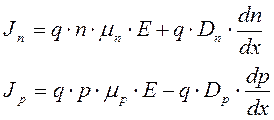. (1.29)

Для трехмерного случая (плотности токов, напряженности полей и градиенты концентраций – векторные величины):

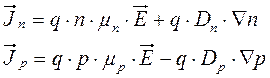. (1.30)

В данном выражении 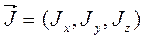, , 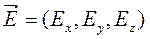а символом 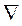обозначен оператор Гамильтона (или набла-оператор), который действует на скалярную функцию как

, .

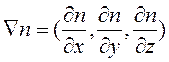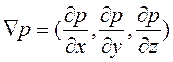Общая плотность тока

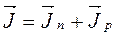. (1.31)

где индекс n относится к электронным компонентам, а индекс p к дырочным.

Уравнения непрерывности:

Уравнения непрерывности записывают отдельно для электронной и дырочной составляющей токов.

В одномерном случае они имеют следующий вид:

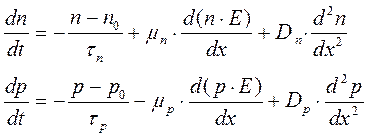(1.32)

Для трехмерного случая в векторной форме:

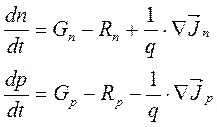. (1.33)

В данном выражении 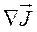есть дивергенция векторного поля .

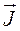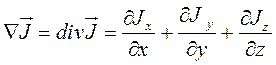. (1.34)

Она характеризует скорость накопления (или рассасывания) носителей заряда в элементарном объеме полупроводника, обусловленную неравенством втекающих и вытекающих потоков носителей.

Часто уравнение непрерывности называют уравнением переноса или законом сохранения массы.

Уравнение Пуассона:

Если величина электрического потенциала j изменяется в теле полупроводника от точки к точке (потенциал пространственно распределен в системе координат X,Y,Z), то напряженность электрического поля есть

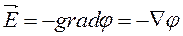. (1.35)

В данной формуле 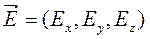, 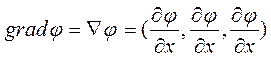- градиент скалярной функции j.

В одномерном случае напряженность поля есть пространственная производная от потенциала, взятая с обратным знаком

. (1.36)

Единица измерения пространственных компонент напряженности Е равна вольт на сантиметр (В/см).

Уравнение, которое определяет взаимосвязь между напряженностью электрического поля E и распределением системы зарядов в исследуемом объеме пространства, называется уравнением Пуассона.

Для одномерного случая уравнение имеет вид:

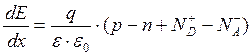, (1.37)

где e₀ – диэлектрическая проницаемость вакуума;

e – относительна диэлектрическая проницаемость материала, из которого сделан полупроводниковый прибор.

Для кремния e равняется 11,7, для арсенида галлия – 13,1, для германия – 16. Величина e₀ равна 8,854×10^-14 Ф/см.

В трехмерном случае

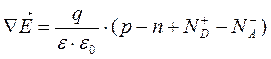. (1.38)

Легко видеть, что если Е=const, то уравнение Пуассона переходит в уравнение электронейтральности

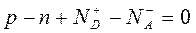. (1.39)

По сути, уравнение Пуассона есть дифференциальная форма записи закона Гаусса: поток вектора напряженности электрического поля через любую замкнутую поверхность равен сумме всех зарядов, заключенных в данном объеме (деленной на e×e₀).

Date: 2015-05-09; view: 2493; Нарушение авторских прав