Примеры поведение эффективного объема, характеризующего степень хаотичности состояния термодинамической системы, при обратимых и необратимых процессах

Феноменологическая термодинамика предсказывает возрастание энтропии, как при изотермическом расширении, так и при возрастании температуры термодинамической системы без увеличения ее объема, и неизменность энтропии (ее сохранение) при адиабатных процессах. Объяснение этих закономерностей должно быть дано не только с точки зрения макроскопически-описательной, феноменологической (то есть через известную формулу Клаузиуса для изменения энтропии dS = dQ/Т), но и с микроскопической точки зрения.

Напомним, что в нашем понимании хаотичность состояния термодинамической системы связана с дисперсией микроскопических характеристик, определяющих состояние, то есть с дисперсией координат и импульсов частиц, образующих термодинамическую систему. Проекции координат и импульсов частиц термодинамической системы рассматриваются как случайные физические величины, и к ним применимы статистические методы вычислений (методы теории вероятностей).

Рассмотрим идеальный газ, каждая молекула которого имеет i степеней свободы. В фазовом пространстве 2i измерений (из которых i измерений отображают собственно координаты молекул, а остальные i - проекции их импульсов) состояние каждой молекулы изображается точкой, имеющей соответствующие проекции на координатные и импульсные оси. Состояние всего газа отображается в таком пространстве роем (множеством) движущихся в фазовом пространстве точек. В условиях теплового равновесия функция распределения плотности этих точек не изменяется с течением времени, хотя точки непрерывно перемещаются в фазовом пространстве, отображая движение (и столкновение) молекул газа. Сама функция распределения плотности дает фазовый портрет термодинамической системы в фазовом пространстве.

За эффективный объем, характеризующий «размытость» фазового портрета термодинамической системы в фазовом пространстве 2i измерений, мы будем принимать произведение стандартов проекций на координатные оси. (Стандарт - корень квадратный из дисперсии, равной, как известно, квадрату среднеквадратичного отклонения случайной величины от ее среднего значения). Здесь в роли случайных величин выступают проекции координат и импульсов отдельных частиц термодинамической системы, взятые в произвольный момент времени.

Таким образом, эффективный объем в фазовом пространстве, связанный с хаотичностью состояния всей термодинамической системы, определяется произведением

DW = Õ(Dq_i·Dp_i),

где через Dq_i и Dp_i обозначены стандарты проекций координат и импульсов на оси координат фазового пространства.

Например, для равновесного состояния идеального газа при температуре Т эффективный объем DW = Const·VT^i/2 (при числе степеней свободы молекулы газа = i), поскольку стандарт, относящийся к любой из пространственных координатных осей, пропорционален размеру вдоль этой оси сосуда с газом, и, следовательно, произведение этих стандартов будет пропорционально объему сосуда. Кроме того, для максвелловского распределения молекул по компонентам скорости (и соответственно, по компонентам импульсов) стандарты распределения (корень квадратный из дисперсии) пропорциональны Т^1/2, так как для гауссова распределения дисперсия обратно пропорциональна показателю экспоненты, что легко вычисляется методами статистической физики.

Степень хаотичности состояния термодинамической системы естественно определять через величину этого эффективного объема. Степень хаотичности увеличивается, если эффективный фазовый объем растет, что и происходит при расширении газа в пространстве (увеличение обычного объема), равно как и при повышении температуры, которое ведет к «расплыванию» максвелловской функции распределения молекул газа по компонентам скорости (и соответственно, импульса), поскольку эта функция имеет вид распределения Гаусса, где абсолютная температура Т стоит в знаменателе отрицательного показателя экспоненты, а дисперсия гауссова распределения, как упоминалось, пропорциональна знаменателю показателя экспоненты.

В природе существуют адиабатные процессы, происходящие без теплообмена термодинамической системы с окружающими телами. При таких процессах энтропия должна сохраняться согласно дифференциальному определению Клаузиусом изменения энтропии dS = dQ/Т = 0, то есть S = Const. В адиабатных процессах, как известно (см. (3.8)), увеличение объема газа сопровождается понижением температуры, и наоборот, уменьшение объема ведет к увеличению температуры системы.

В фазовом пространстве адиабатные процессы должны отображаться такой трансформацией эффективного фазового объема (характеризующего, как мы предполагаем, хаотичность состояния), при которой увеличение дисперсии проекций координат должно полностью компенсироваться уменьшением дисперсии проекций импульсов с тем, чтобы эффективный объем при этом сохранялся. Понятно, что это следствие адиабатного процесса, проявляющееся на микроскопическом уровне (сохранение эффективного объема у фазового портрета), должно быть связано с уравнением адиабаты, известным из феноменологической, макроскопически-описательной термодинамики.

Для демонстрации выполнения этого условия (сохранение этого эффективного объема у частиц при обратимых изоэнтропных процессах) воспользуемся, как обычно, моделью идеального газа. Уравнение адиабаты для идеального газа в координатах температура-объем (T,V), как известно, имеет вид TV ^g-1 = Const (3.8). В этом уравнении показатель адиабаты g, входящий в показатель степени объема, имеет, как известно, смысл отношения теплоемкостей газа в изобарном (С_р) и изохорном (С_V) процессах, и может быть выражен через число степеней свободы отдельной молекулы идеального газа как g = (i +2)/i, поскольку С_р = (i +2)R/2 и С_V = iR/2 (смотрите Приложение2). Поскольку (g - 1) = 2/i, то уравнение адиабаты, выраженное через число степеней свободы молекулы, принимает вид TV^2/i = Const. Возведя обе стороны этого равенства в степень i/2, получаем окончательно выражение для адиабаты в необходимой для дальнейшего форме

VТ^i/2 = Const.

Так как ранее уже было показано, что эффективный объем, характеризующий размытость фазового портрета идеального газа имеет вид W = Const·VT^i/2, то для адиабатного обратимого (и поэтому изоэнтропного) процесса идеального газа получаем

DW = Const,

то есть постоянство эффективного объема в обратимых адиабатных процессах, что и требовалось показать.

Для цикла Карно, состоящего из двух изотерм и двух адиабат, (см. Рис.3) это означает, что возрастание эффективного фазового объема при получении рабочим телом (идеальным газом) тепла от нагревателя на участке 1-2 должно равняться уменьшению эффективного объема при передаче тепла холодильнику на участке 3-4. Покажем, что это действительно так.

Прирост эффективного фазового объема при изотермическом (Т = Т_н) расширении газа dW_н = dV_нDр_н, где dV_н – увеличение объема при расширении во время контакта с нагревателем, Dр_н – произведение стандартов проекций импульсов, сохраняющихся в этом процессе и пропорциональных корню квадратному из температуры. (В этих формулах нижние индексы н и х отображают контакты с нагревателем и холодильником).

Таким образом, прирост эффективного фазового объема при изотермическом расширении

dW_н = Const·(V_н2 - V_н1)Т_н^i/2.= Const·V_н1(V_н2/V_н1 -1)Т_н^i/2.

Аналогично для изотермического сжатия при контакте с холодильником

dW_х = - Const· (V_х3 - V_х4)Т_х^i/2 = - Const·V_х4(V_х3/V_х4- 1)Т_х^i/2,

где знак минус означает уменьшение объема.

Осталось убедиться, что по модулю изменения объемов равны, так как газ должен вернуться в первоначальное состояние. Для этого вспомним полученное при рассмотрении цикла Карно соотношение V_н2/V_н1 = V_х3/V_х4 а также выражение для адиабаты через число степеней свободы молекулы газа VТ^i/2 = Const. Поскольку 1-я и 4-я точки на диаграмме цикла Карно в координатах давление-объем связаны адиабатой, то V_н1Т_н^i/2 = V_х4Т_х^i/2. Если учесть эти уравнения, то очевидно равенство (по модулю) изменений эффективных фазовых объемов в цикле Карно на изотермических участках, dW_н = - dW_х, что и требовалось показать. Таким образом, рабочее тело (идеальный газ) при завершении цикла Карно возвращается к первоначальному эффективному фазовому объему, характеризующему хаотичность его состояния.

Таким образом, мы убедились, что эффективный объем ведет себя в обратимых процессах аналогично энтропии. Будем для определенности считать его пропорциональным энтропии.

Теперь обратимся к рассмотрению поведения эффективного объема при самопроизвольном выравнивании температур, вследствие теплообмена через теплопроводящую перегородку, двух идентичных количеств газа, отличающихся только температурами, причем Т₁ > Т₂. Мы знаем из термодинамики, что этот процесс необратим и энтропия должна возрасти. Посмотрим, справедливо ли это для эффективного объема.

Энтропия, как аддитивная величина, для первоначального состояния (с разными температурами, но одинаковыми объемами) находится как сумма энтропий этих газов S⁽¹⁾ = S₁⁽¹⁾ + S₂⁽¹⁾, или

S⁽¹⁾ = Const{ΠDq_i1Dp_i1 + SΠq_i2Dp_i2} = Const{ΠDq_i[ΠDp_i1⁽¹⁾+ ΠDp_i2⁽¹⁾]},

так как объемы газов одинаковы, и, следовательно, одинаков разброс по координатам (множитель перед прямой скобкой пропорционален объему каждого из газов). Значит, энтропия первоначального состояния

S⁽¹⁾ = Const·[ΠDp_i1⁽¹⁾+ ΠDp_i2⁽¹⁾].

После замены теплоизолирующей перегородки на теплопроводящую и выравнивания температур до средней температуры q = (Т₁+Т₂)/2, новое значение энтропии, вычисленное через эффективные объемы, будет (при сохранении множителя перед прямой скобкой)

S⁽²⁾ = S₁⁽²⁾ + S₂⁽²⁾ = Const·[Dp_i1⁽²⁾+ Dp_i2⁽²⁾]= Const·[2Dp_i1⁽²⁾],

так как после выравнивания температур усредненный разброс импульсов у молекул в разных отсеках теперь одинаков (а не только разброс по координатам).

По свойству дисперсии гауссова распределения стандарт импульса Dp_i ~ √Т и, следовательно, энтропия начального состояния S⁽¹⁾ = Const·(ÖT₁+ÖT₂), а S⁽²⁾ = Const·[2Öq] = Const·[ ].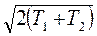

Теперь мы можем найти отношение начального значения энтропии к её конечному значению S⁽¹⁾/ S⁽²⁾ = (ÖT₁+ÖT₂)/ .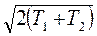

Для утверждения, что эффективный объем возрастает после выравнивания температур, осталось показать, что правая часть равенства меньше единицы. Для этого возводим правую часть в квадрат, делим числитель на знаменатель и получаем выражение

½ [1 + (ÖT₁ÖT₂)/{(T₁+T₂)/2}],

где в числителе дроби в квадратной скобке оказалось среднее геометрическое, а в знаменателе - среднее арифметическое первоначальных температур, но первое (геометрическое), как известно, всегда меньше второго (арифметического). Следовательно, число в квадратной скобке меньше двух, и значит правая часть уравнения для отношения энтропий меньше единицы, и S⁽¹⁾ < S⁽²⁾. Тем самым показано, что эффективный объем ведет себя при необратимых процессах выравнивания температур так же, как и энтропия, то есть возрастает, как и должно быть, если этот объём действительно является наглядным отображением энтропии в фазовом пространстве.

Как видно из всех рассмотренных примеров, эффективный объем ведет себя как в обратимых, так и в необратимых процессах так же как энтропия согласно предсказаниям термодинамики.

Согласно квантовой статистике фазовое пространство дискретно и делится на элементарные ячейки размером (hⁱ). Чем больше эффективный объем, тем больше статистический вес термодинамической системы W, который в соответствии с квантовой статистикой будет у нас равен частному от деления эффективного объема на постоянную Планка в степени, равной числу степеней свободы, то есть на (hⁱ), и значит, больше энтропия S = k·lnW.

Таким образом, сообщая термодинамической системе теплоту, мы тем самым увеличиваем степень хаотичности ее состояния, «раздувая» эффективный объем, увеличиваем статистический вес системы и наращиваем энтропию.

Из всего вышеизложенного следует, что энтропии может быть сопоставлен наглядный образ – эффективный объем в фазовом пространстве.

Рекомендуемая литература

1. Леонтович М.А. Введение в термодинамику. - М.: ГИТТЛ, 1952. 200с.

2. Тер Хаар Д., Вергелянд Г. Элементарная термодинамика. - М.: Мир,1968. 220с.

3. Сивухин Д.В. Общий курс физики. Т.2. Термодинамика и молекулярная физика. - М.: Наука, 1975. 552с.

Date: 2015-05-09; view: 657; Нарушение авторских прав