Схема опыта Юнга

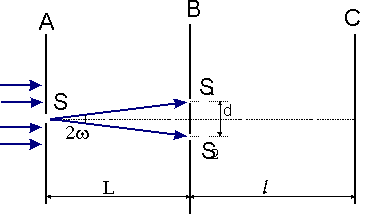
Прошедший через отверстие свет вследствие дифракции образует расходящийся пучок, который падает на второй экран B с двумя малыми отверстиями S 1 и S 2, расположенными близко друг к другу на равных расстояниях от S. Эти отверстия действуют как вторичные точечные синфазные источники, и исходящие от них волны, перекрываясь, создают интерференционную картину, наблюдаемую на удаленном экране C. Положение светлых и темных полос в ней можно находить, пользуясь монохроматической идеализацией. Расстояние между соседними полосами равно(см. Интерференция монохроматического света).

Трудности наблюдения интерференции света в таком опыте связаны с тем, что длина волны видимого света очень мала. При см и расстоянии d между отверстиями S1 и S2, равном всего 0,5 мм, ширина интерференционных полос составляет только 1 мм при удалении экрана C на 1 м от отверстий. Измеряя ширину интерференционных полос, Юнг в 1802 г. впервые определил длины световых волн для разных цветов, хотя эти измерения и не были точными.

Введение дополнительного отверстия S (оно необходимо для когерентного возбуждения источников S1 и S2, см Роль конечных размеров источника света) резко уменьшает световой поток, что также затрудняет осуществление этого опыта. Интенсивность наблюдаемой в опыте Юнга интерференционной картины можно заметно увеличить, если вместо точечных отверстий S, S1 и S2 в экранах применить узкие длинные параллельные между собой щели. Вид полос вблизи центра интерференционного поля будет при этом таким же, как при использовании точечных отверстий. Поясним это. Если точечное отверстие S перемещать перпендикулярно плоскости чертежа на рисунке, то интерференционные полосы на экране C, получаемые от точечных отверстий S1 и S2, будут просто смещаться вдоль своих направлений, т.е. также перпендикулярно плоскости чертежа. Поэтому замена отверстия S длинной щелью, т.е. непрерывной цепочкой точечных некогерентных источников, не приведет к ухудшению четкости интерференционных полос, по крайней мере в той области, где их кривизна незначительна. Аналогично, не ухудшит четкости и замена отверстий S1 и S2 на узкие длинные щели, перпендикулярные плоскости чертежа на рисунке.

Увеличение размера первого отверстия или щели S в плоскости чертежа (т.е. увеличение ширины) неизбежно приводит к уменьшению контрастности (видности) интерференционных полос (см. Роль конечных размеров источника света). В современной демонстрационной модификации опыта Юнга в качестве источника света используют лазер. При этом для когерентного возбуждения вторичных источников S1 и S2 необходимость во вспомогательном отверстии S отпадает, так как в лазерном излучении световые колебания когерентны по всему поперечному сечению пучка (высокая пространственная когерентность лазерного излучения), и щели вводят непосредственно в пучок лазерного излучения.

Бипризма Френеля, представляющая собой две призмы, соединенные основаниями, формирует два мнимых источника. Преломляющий угол обеих половин одинаков и (у бипризмы хорошего качества) чрезвычайно мал: ребро ее отличается от 180° на единицы угловых минут. В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы (см. рисунок).

Бипризма Френеля

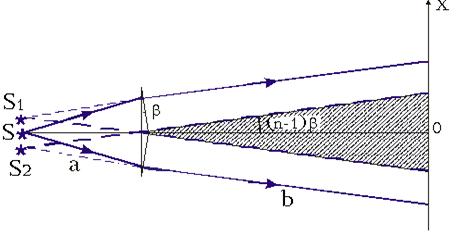
Можно считать, что здесь образуются два близких мнимых изображения S1 и S 2 источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол (n-1)S.

Бизеркала Френеля составляют плоский угол (близкий к 180°) и позволяют за счет отражения сформировать два мнимых источника. Как и в любой системе плоских зеркал, все три источника находятся на одинаковом расстоянии от ребра плоского угла (на окружности с центром в ребре). Хотя при отражении от зеркала происходит фазовый сдвиг, дополнительной разности фаз не возникает - ведь сдвигаются фазы обоих пучков.

Другой интерференционный опыт, аналогичный опыту Юнга, но в меньшей степени осложненный явлениями дифракции и более светосильный, был осуществлен Френелем в 1816 г. Две когерентные световые волны получались в результате отражения от двух зеркал, плоскости которых наклонены под небольшим углом друг к другу (см. рисунок).

Зеркала Френеля

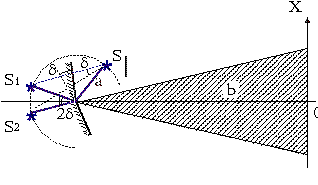
Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются, возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой. Для расчета освещенности I(x) экрана можно считать, что интерферирующие волны испускаются вторичными источниками S1 и S2, представляющими собой мнимые изображения щели S в зеркалах. Поэтому I(x) будет определяться формулой двухлучевой интерференции, в которой расстояние l от источников до экрана следует заменить на a + b, где a - расстояние от S до ребра зеркал, b - расстояние от ребра до экрана (см. рисунок). Расстояние d между вторичными источниками равно. Поэтому ширина интерференционной полосы на экране равна .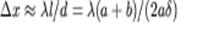

17. Способы получения когерентных пучков в оптике делением амплитуды. Интерференция от плоско–параллельной пластинки. Полосы равного наклона.

Пусть на плоскопараллельную пластину толщиной h и с показателем преломления n падает рассеянный монохромати- ческий свет с длиной волны λ. Из условия Δ = 2nh cosβ следу- ет, что при n,h = const разность хода зависит только от угла па- дения лучей β. Очевидно, что лучи, падающие под одним уг- лом, будут иметь одну и ту же разность хода. Если параллельно пластине разместить линзу L, в фокальной плоскости которой расположен экран Э, то эти лучи соберутся в одной точке экрана (рис.2.10). В рассеянном свете имеются лучи самых разных направлений. Лучи, падаю- щие на пластину под углом α 1, соберутся на экране в точке Р 1, интенсивность света в которой определяется разностью хода Δ. Путем не- сложных расчетов можно получить, что Δ= − 2 22 hn s i nα 1. Лучи, падающие на пластину под углом α 1, но в другой плоскости, будут иметь та- кую же разность хода и соберутся в другой точке, но на таком же расстоянии от центра экрана. Таким образом, лучи, падающие на пластину во всевозможных плоскостях, но под углом α 1, создают на экране совокупность одинаково освещенных точек, расположенных на окружности с центром в точке О. Аналогично, лучи, падающие под другим углом α 2, создадут на экране совокупность Э Р 2 Р 1 0 L α 2 α 1 h Рис.2.10. Рис.2.10 28 одинаково освещенных точек, но расположенных на окружности другого радиуса. Следовательно, на экране будет наблюдаться система концентрических окружностей, называемых линиями равного наклона. Поскольку интерферирующие лучи идут к эк- рану параллельным пучком, то говорят, что линии равного на- клона локализованы в бесконечности. Для наблюдения их пользуются линзой (роль линзы может играть хрусталик глаза).

Date: 2015-05-08; view: 1580; Нарушение авторских прав