Основное уравнение квантовой механики

1926г. Уравнение Шредингера.

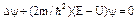
m- масса частицы.

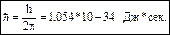
E- полная энергия частицы.

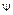- пси-функция (волновая функция).

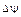- оператор Лапласа.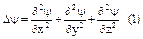

С помощью 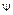описывается поведение микрочастицы в данный момент времени. 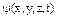, так как это поведение носит вероятностный характер, то с помощью 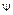надо умерь рассчитывать вероятность обнаружения микрочастицы в данном объеме пространства. А, так как вероятность действительная и положительная, то за меру вероятности берут не саму 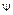, а квадрат ее модуля.

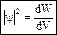- плотность вероятности (вероятность [W] обнаружения частицы в данный момент времени в единичном объеме)

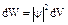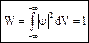; - вероятность достоверного события.

Итак. Решив уравнение, получаем значение 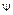; зная ее можем рассчитать вероятность нахождения частицы в данный момент времени в данном объеме пространства. Чтобы 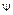была объективной характеристикой поведения микрочастицы, она должна обладать следующими свойствами:

1. Непрерывность.

Разрыв 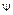может приводить к неверным результатам при расчете вероятности.

2. Однозначность, чтобы не было неоднозначности при расчете вероятности.

3. Конечность, потому что вероятность не может быть больше 1.

В теории дифференциального уравнения подобного типа (2-го порядка частных производных) доказывается, что решения, удовлетворяющие свойствам непрерывности, имеют место только при определенных значениях параметра, входящего в это уравнение. Таким параметром в данном уравнении является Е (энергия микрочастицы). Следовательно, из уравнения Шредингера без каких-либо постулатов вытекает дескретный ряд значений полной энергии микрочастицы.

Применение уравнения (1) к атому водорода.

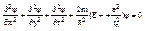
Решение уравнения дает:

Date: 2015-05-08; view: 457; Нарушение авторских прав