Принцип неопределенности. Классическая механика

Постановка задачи.

Классическая механика.

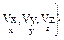Эти характеристики достоверно известны одновременно в данный момент времени.

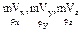, px -проекция момента импульса на ось Х. 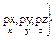сопряженные параметры

Можно ли таким же образом описывать поведение микрочастиц? Нет, так как природа процессов различная.

Ответ находят, рассматривая опыт по дифракции электронов на щели.

Рис.1.7.

AB= 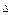x - ширина щели (расстояние между узлами кристаллической решетки).

Если на экране появилась вспышка, то можно утверждать, что электрон прошел щель. При этом ширина щели (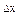) есть неопределенность местонахождения электрона в момент прохождения щели.

Если сужать щель (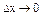) то получим достоверное значение координаты х электрона в момент прохождения щели.

Благодаря волновым свойствам электрона можно утверждать, что электрон, пройдя щель, дальше движется внутри конуса с углом раствора .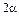

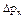-неопределенность p_x электрона при прохождении через щель. .

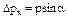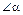- угол первого дифракционного минимума на щели.

Итак.

1. Если 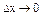, то есть х.

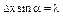
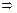
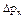– возрастает, -возрастает.

2. Если 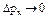, то есть p_х.

.

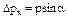
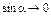
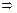
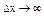Следовательно, координата и спряженный импульс не могут быть одновременно неопределены не в силу технических невозможностей, а в силу того, что эти две величины не являются характеристиками микрочастицы потому что микрочастица, в отличие от классической частицы, обладает еще и волновыми свойствами. Как только мы хотим применить к микрочастице характеристики классической часитцы, возникает неопределенность.

Если все же хотим описать поведение микрочастицы с помощью координаты и сопряженного импульса, то это можно сделать только в следующих пределах:

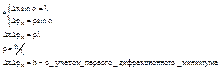
С учетом дифракционных минимумов большего порядка соотношение будет следующим: 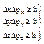- соотношение неопределенностей. Является следствием волновых свойств микрочастиц.

Соотношение неопределенностей поставили последнюю точку в споре о том, можно ли использовать законы Ньютона в микромире. Нет.

Date: 2015-05-08; view: 461; Нарушение авторских прав