Краткая теория. Наблюдение процессов в природе и технике показывает, что протекание их в противоположных направлениях приводит к существенно различным результатам

Наблюдение процессов в природе и технике показывает, что протекание их в противоположных направлениях приводит к существенно различным результатам. Примерами могут служить нагревание и охлаждение тел, смешивание и разделение растворов, заряд и разряд аккумуляторов и т. д.

Важной характеристикой протекания процессов является их обратимость. Обратимым называется процесс, для которого возможен обратный переход из конечного состояния в начальное через те же промежуточные состояния, что и в прямом процессе, но без изменения состояния окружающей среды. Процессы, не удовлетворяющие этому определению, называются необратимыми.

Рассмотрим несколько примеров.

1. Колебания маятника в отсутствие затухания есть полностью обратимый процесс. Если на маятник действуют силы трения, процесс становится необратимым, т.к. часть механической энергии маятника при каждом колебании переходит в тепловую. Можно заставить колебаться маятник сколь угодно долго, однако для этого необходимо пополнять энергию системы извне, действуя внешней силой и совершая работу.

2. При смешивании химического соединения с растворителем наблюдается диффузия растворенного вещества, приводящая к выравниванию его концентрации во всех частях растворителя. Это необратимый процесс, т.к. обратный процесс - самопроизвольного сбора растворенного вещества в какой-либо части растворителя - не наблюдается никогда. Для сбора растворителя необходимо воздействовать на систему извне, совершая при этом работу: например, испарить растворитель.

3. Пусть в состав изолированной системы входят два тела, нагретых до различной температуры. Тогда в системе самопроизвольно начнется процесс перехода энергии от более нагретого тела к менее нагретому телу, и никогда самопроизвольно не будет происходить обратный процесс. Передача тепла от менее нагретого к более нагретому телу возможна только при выполнении работы над системой.

Можно утверждать, что механические процессы, не сопровождающиеся диссипацией (рассеянием) механической энергии, обратимы, а процессы в системах с большим количеством частиц (макросистемах) всегда необратимы.

Определение основных параметров состояния системы (давления р, объема V и температуры Т) не позволяет ответить на вопрос, обратим ли процесс и в каком направлении он может происходить. Нельзя выяснить вопрос об обратимости и возможном направлении протекания процесса и из первого начала термодинамики:

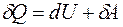, (1)

т.к. приращение внутренней энергии dU есть полный дифференциал, а внутренняя энергия U есть функция состояния системы (ее изменение зависит только от температуры системы в начальном и конечном состоянии и не зависит от пути перехода), работа же зависит от того, посредством какого процесса система переходит из одного состояния в другое. Другими словами, работа А и количество теплоты Q являются характеристиками не отдельного состояния системы, а совершаемого ею процесса.

Для выяснения вопроса об обратимости и направлении протекания процессов в термодинамике наряду с основными параметрами р, V, T вводится энтропия S – такая функция состояния термодинамической системы, дифференциал которой dS в элементарном обратимом процессе равен отношению бесконечно малого количества теплоты 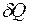, сообщенного системе, к абсолютной температуре Т системы:

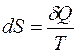. (2)

Из (2) следует, что физический смысл имеет только изменение энтропии, для

макроскопических процессов оно равно

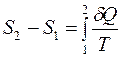, (3)

где S ₂, S ₁ – энтропия в конечном и начальном состоянии системы соответственно.

За нуль энтропии может быть выбрано ее значение для системы в любом исходном состоянии. Практически за нуль энтропии выбирают ее значение для системы при абсолютном нуле температуры.

Энтропия – величина аддитивная: энтропия макросистемы равна сумме энтропий ее отдельных частей:

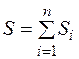. (4)

Больцман показал, что энтропия системы зависит от вероятности 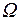реализации данного состояния системы:

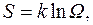(5)

где термодинамическая вероятность 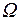определяет число микросостояний, соответствующих одному макросостоянию системы; k = 1,38·10^-23 Дж/К – постоянная Больцмана.

Под макросостоянием понимается задание определенных значений макропараметров системы (например, р, V, T). Под микросостоянием понимается каждое конкретное распределение микрочастиц системы по положению (координатам) и скоростям.

Замкнутой (изолированной) называется термодинамическая система, которая не обменивается ни энергией, ни веществом с другими системами.

В соответствии со вторым началом термодинамики при любых процессах в замкнутой системе энтропия не убывает:

Δ S = S ₂ – S ₁ ³ 0, (6)

где S ₂, S ₁ – энтропия в конечном и начальном состоянии системы соответственно.

При обратимых процессах ΔS = 0, при необратимых ΔS > 0.

Из сравнения (5) и (6) следует, что в любых процессах в замкнутой системе вероятность конечного состояния не меньше вероятности начального состояния.

Это утверждение не является абсолютным. Оно указывает лишь наиболее вероятное направление протекание процессов. Однако расчеты и опыт показывают, что вероятность протекания процессов в противоположном направлении настолько незначительна, что такую возможность просто нет смысла учитывать.

Таким образом, расчет изменения энтропии позволяет выяснить направление протекания процесса в ней. Для определения энтропии системы можно воспользоваться ее связью с другими термодинамическими параметрами – давлением р, объемом V, температурой T, которые могут быть определены в эксперименте.

При передаче тепла от одного тела к другому, когда работа не совершается (например, при изохорном процессе в идеальном газе), элементарное количество теплоты

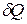= сmdT, (7)

где с – удельная теплоемкость вещества, m - масса тела. Тогда изменение энтропии в данном процессе в соответствии с (3) равно

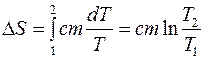, (8)

где Т ₁, Т ₂ - температура тела начальном и конечном состоянии соответственно.

В лабораторной работе необходимо определить изменение энтропии замкнутой системы, включающей калориметр, воду, испытуемое тело и термометр, при теплообмене между ними. Пусть калориметр, вода и термометр в начале опыта имеют температуру Т ₁, испытуемое тело – Т ₂, а по достижении теплового равновесия устанавливается одинаковая для всех них температура Т ₀.

В соответствии с (8) изменения энтропии калориметра Δ S _к, воды Δ S _в, тела Δ S _т и термометра Δ S _тм равны:

Δ S _к = с _к m _к 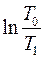; Δ S _в = с _в m _в 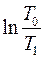; Δ S _т = с _т m _т 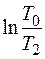; Δ S _тм = с _тм m _тм 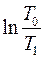, (9)

где m _тм, с _тм – масса и удельная теплоемкость термометра соответственно.

В соответствии со свойством аддитивности (4) изменение энтропии системы равно

Δ S = Δ S _к + Δ S _в + Δ S _т +Δ S _тм. (10)

Установившуюся в результате теплообмена температуру Т ₀ в системе можно рассчитать с помощью уравнения теплового баланса

Δ Q _к + Δ Q _в + Δ Q _т +Δ Q _тм = 0, (11)

из которого с учетом (7) имеем:

с _к m _к (Т ₀ – Т ₁) + с _в m _в (Т ₀ – Т ₁)+ с _т m _т (Т ₀ – Т ₂) + с _тм m _тм (Т ₀ – Т ₁) = 0, (12)

откуда

.

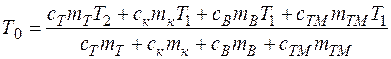(13)

Date: 2015-05-08; view: 591; Нарушение авторских прав