Дифракционно-ограниченная система

В геометрической оптике под идеальным изображением точки понимается вершина гомоцентрического пучка. Если после прохождения через оптическую систему не все лучи пучка пересекаются в одной точке, то говорят, что система обладает аберрациями. Источником аберраций может служить дисперсия стекла – зависимость показателя преломления от длины волны (хроматическая аберрация), а также различие в оптической длине пути между точками А и А’ (рис.1) для разных лучей одной и той же длины волны, проходящих через систему (сферическая аберрация, кома и другие монохроматические аберрации) [1,7].

Аберрации в оптических системах могут частично (а в некоторых случаях даже полностью) устранены путем подбора кривизны поверхностей линз, а также путем сочетания линз из стекол с разными показателями преломления. Хорошо исправленная в отношении аберраций система может практически не отличаться от идеальной, но даже такая система не может дать изображения точки в виде точки. Причиной этого является дифракция, не учитываемая геометрической оптикой. Дифракция приводит к тому, что даже безаберрационная система дает изображение точки в виде пятна рассеяния, хотя и малых, но конечных размеров. В результате изображения двух близлежащих точек могут слиться, и точки перестанут быть различимы. В этом случае говорят о дифракционно-ограниченной оптической системе. Очевидно, что наличие аберрации дополнительно снижает разрешающую способность.

Распределение освещенности в дифракционном пятне рассеяния может быть вычислено на основе принципа Гюйгенса-Френеля. Допустим, что из оптической системы выходит строго гомоцентрический пучок лучей, которому соответствуют вогнутые сферические волновые поверхности с центром в точке A’ (рис.7). Согласно принципу Гюйгенса-Френеля каждую точку волновой поверхности нужно рассматривать как центр когерентных вторичных волн, из которого колебания доходят до окрестности точки A’. Распределение освещенности вокруг A’ в плоскости изображения является результатом интерференции этих вторичных волн. Теория показывает, что ограничение пучка лучей, выходящих из осевой точки предмета А, которое возникает в оптической системе, приводит к сложной структуре пятна рассеяния вблизи изображения A’. Пространственное распределение интенсивности I(r) в плоскости изображения описывается функцией Бесселя первого рода первого порядка J₁(x)

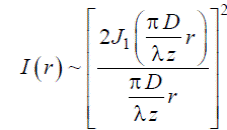
где l- длина световой волны, D- диаметр так называемого выходного зрачка оптической систем, z - расстояние от зрачка до плоскости изображения (см. рис.7).

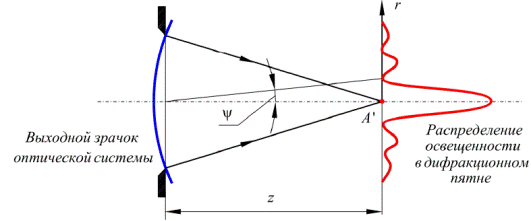
Рис.7. Дифракция света на выходном зрачке оптической системы

Дифракционная картина состоит из центрального кружка, в котором освещенность быстро убывает от центра к периферии, и из ряда колец, разделенных темными промежутками, в которых освещенность падает до нуля. В центральном дифракционном кружке, называемом кружком Эри, сосредоточено около 84% всей энергии в дифракционной картине, и его диаметр фактически определяет размер дифракционного изображения точки.

Радиус дифракционного кружка в угловой мере может быть определен по формуле

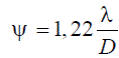(10)

Если две светящиеся точки расположены близко друг к другу, то их дифракционные изображения будут частично перекрываться (рис.8). При условии взаимной некогерентности световых волн от точек A и B предмета считается, что эти точки изображаются системой еще раздельно, если центр дифракционного кружка в изображении В совпадает с краем дифракционного кружка в изображении А. Суммарная кривая интенсивности будет иметь два максимума и один минимум (рис.9), разделяющий два изображения.

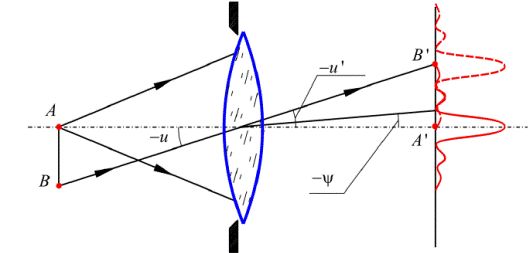
Рис.8. Частичное перекрытие дифракционных изображений двух близко расположенных точек предмета

Если 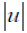- угловое расстояние между точками А и В (см. рис.7), то условие разрешения имеет вид 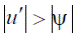. Это положение носит название критерия Релея. Как следует из (10), разрешающая способность зависит от длины волны излучения и диаметра выходного зрачка системы (диаметра действующего отверстия системы).

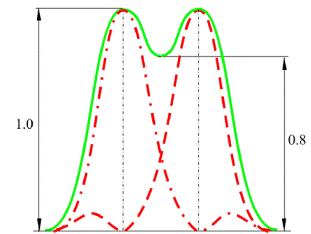
Рис.9. Суммарное распределение интенсивности света в дифракционном изображении двух некогерентных точечных источников, находящихся на пределе разрешения по Релею

Для практического определения разрешающей способности системы используют оптическую схему, ход лучей в которой приведен на рис.6. Объект, размеры которого l известны с большой точностью, помещают в фокальной плоскости коллиматора (система 1). Его изображение, размер которого l’ связан с l формулой (9), возникает в задней фокальной плоскости испытуемой системы (система 2) и через микроскоп рассматривается глазом. Измерения заключаются в подборе объекта, изображение которого находилось бы на грани разрешения.

В качестве меры разрешающей способности оптической системы обычно используется либо непосредственно величина минимально разрешимого отрезка l (объективы микроскопов), либо обратная ей величина - число разрешенных 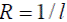линий на 1 мм, либо угол 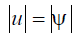, связанный с l формулой (7) (объективы телескопов).

Для характеристики фотообъективов используется также величина - число разрешенных линий на 1 мм в плоскости изображения. Используя формулы (9) и (10) и применяя критерий Релея 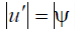, получим

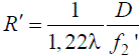
Отношение D/f2’ называют относительным отверстием системы. Соотношение между R и R’ можно найти при помощи формулы (9)

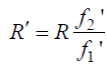(11)

Разумеется, разрешающая способность используемых в измерительной установке коллиматора и микроскопа должна превышать разрешающую способность испытуемой оптической системы. При этом увеличение микроскопа должно быть таким, чтобы угловые размеры создаваемого им изображения заведомо превышали предел разрешения глаза (1.4 угловые секунды).

Определение разрешающей способности оптической системы осуществляется при помощи специальных испытательных объектов, называемых мирами.

Используемые в работе штриховые миры представляют собой системы черных полос, нанесенных на прозрачную стеклянную пластинку. Период штрихов миры l (так же как период дифракционной решетки) включает в себя ширину черной полосы и ширину промежутка. Каждая испытательная мира представляет собой квадратную таблицу, которая состоит из 25 больших квадратов (элементов), отличающихся по периоду штрихов (рис.10). Элементы миры нумеруются слева направо, номера проставлены только около крайних элементов. При увеличении номера элемента период штрихов убывает на 6%. В каждом элементе имеются 4 малых квадрата, в которых штрихи имеют одинаковый период, но ориентированы в различных направлениях.

Рис.10. Изображения элементов миры Полный испытательный комплект состоит из 5 мир. Каждая мира характеризуется базой В – расстоянием, заданным с большой точностью между двумя специальными рисками, нанесенными по краям миры (рис.10).

Основные характеристики испытательных мир приведены в таблице 1.

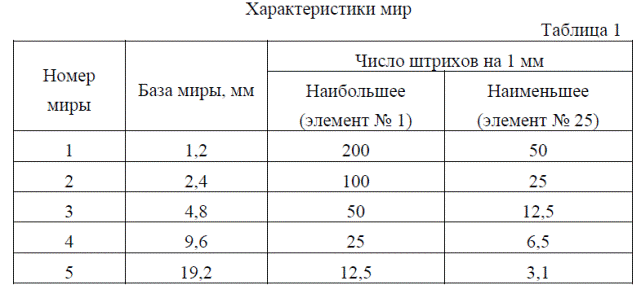
Число штрихов на 1 мм RN для элемента миры с номером N задается через ее базу В по формуле:

Где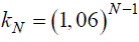

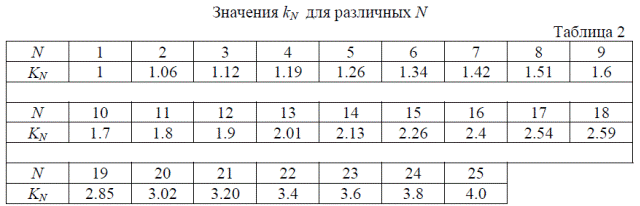
Значения kN приведены в табл.2. Пользуясь выражением (12) и табл. I и 2, можно определить величину RN для всех элементов любой миры.

Угловое расстояние u между соседними штрихами миры, помещенной в фокальной плоскости коллиматора, можно найти, используя соотношения (7) и (10). Принимая во внимание, что угол u мал, и переходя от радианной меры к градусной, получим

Заметим, что значения u для всех элементов испытательных мир приведены в описании к оптической скамье ОСК-2, при помощи которой выполняется экспериментальная часть работы.

Date: 2015-05-08; view: 2437; Нарушение авторских прав