Статистический критерий - это правило (формула), по которому определяется мера расхождения результатов выборочного наблюдения с высказанной гипотезой Н0

Статистический критерий, как и всякая функция от результатов наблюдения, является случайной величиной и в предположении справедливости нулевой гипотезы Н₀ подчинена некоторому хорошо изученному (и затабулированному) теоретическому закону распределения с плотностью распределения f(k).

Выбор критерия для проверки статистических гипотез может быть осуществлен на основании различных принципов. Чаще всего для этого пользуются принципом отношения правдоподобия, который позволяет построить критерий наиболее мощный среди всех возможных критериев. Суть его сводится к выбору такого критерия К с известной функцией плотности f(k) при условии справедливости гипотезы Н₀, чтобы при заданном уровнем значимости α можно было бы найти критическую точку К_кр. распределения f(k), которая разделила бы область значений критерия на две части: область допустимых значений, в которой результаты выборочного наблюдения выглядят наиболее правдоподобными, и критическую область, в которой результаты выборочного наблюдения выглядят менее правдоподобными в отношении нулевой гипотезы Н₀.

Если такой критерий К выбран, и известна плотность его распределения, то задача проверки статистической гипотезы сводится к тому, чтобы при заданном уровне значимости α рассчитать по выборочным данным наблюдаемое значение критерия К_набл. и определить является ли оно наиболее или менее правдоподобным в отношении нулевой гипотезы Н₀.

Проверка каждого типа статистических гипотез осуществляется с помощью соответствующего критерия, являющегося наиболее мощным в каждом конкретном случае. Например, проверка гипотезы о виде закона распределения случайной величины может быть осуществлена с помощью критерия согласия Пирсона χ²; проверка гипотезы о равенстве неизвестных значений дисперсий двух генеральных совокупностей - с помощью критерия F - Фишера; ряд гипотез о неизвестных значениях параметров генеральных совокупностей проверяется с помощью критерия Z - нормальной распределенной случайной величины и критерия T - Стьюдента и т.д.

Значение критерия, рассчитываемое по специальным правилам на основании выборочных данных, называется наблюдаемым значением критерия (К_набл.).

Значения критерия, разделяющие совокупность значений критерия на область допустимых значений (наиболее правдоподобных в отношении нулевой гипотезы Н₀) и критическую область (область значений, менее правдоподобных в отношении таблицам распределения случайной величины К, выбранной в качестве критерия, называются критическими точками(К_кр.).

Областью допустимых значений (областью принятия нулевой гипотезы Н₀) называют совокупность значений критерия К, при которых нулевая гипотеза Н₀ не отклоняется.

Критической областью называют совокупность значений критерия К, при которых нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

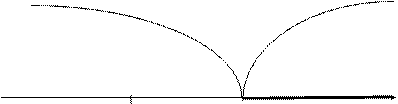
Если конкурирующая гипотеза - правосторонняя, например, Н₁: а > а₀, то и критическая область - правосторонняя (рис 1). При правосторонней конкурирующей гипотезе критическая точка (К_{кр. правосторонняя}) принимает положительные значения.

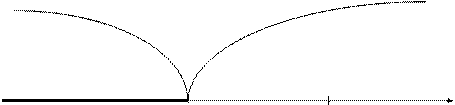
Если конкурирующая гипотеза - левосторонняя, например, Н₁: а < а₀, то и критическая область - левосторонняя (рис 2). При левосторонней конкурирующей гипотезе критическая точка принимает отрицательные значения (К_{кр. левосторонняя}).

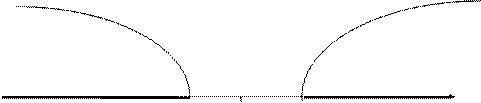
Если конкурирующая гипотеза - двусторонняя, например, Н₁: а ¹ а₀, то и критическая область - двусторонняя (рис 3). При двусторонней конкурирующей гипотезе определяются две критические точки (К_{кр. левосторонняя} и К_{кр. правосторонняя}).

Область допустимых Критическая

значений область

К

0 К_кр.

Рис 8.1. Правосторонняя критическая область.

Критическая Область допустимых

область значений

К

-К_кр. 0 К_кр.

Рис 8.2. Левосторонняя критическая область.

Критическая Область допустимых Критическая

область значений область

К

-К_кр. 0 К_кр.

Рис 8.3. Двусторонняя критическая область.

Основной принцип проверки статистических гипотез состоит в следующем:

- если наблюдаемое значение критерия (К_набл.) принадлежит критической области, то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁;

- если наблюдаемое значение критерия (К_набл.) принадлежит области допустимых значений, то нулевую гипотезу Н₀ нельзя отклонить.

Можно принять решение относительно нулевой гипотезы Н₀ путем сравнения наблюдаемого (К_набл.) и критического значений критерия (К_кр.).

При правосторонней конкурирующей гипотезе:

Если К_набл. £ К_кр., то нулевую гипотезу Н₀ нельзя отклонить;

если К_набл. > К_кр., то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁.

При левосторонней конкурирующей гипотезе:

Если К_набл. ³ - К_кр., то нулевую гипотезу Н₀ нельзя отклонить;

если К_набл. < - К_кр., то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁.

При двусторонней конкурирующей гипотезе:

Если - К_кр. £ К_набл. £ К_кр., то нулевую гипотезу Н₀ нельзя отклонить;

если К_набл. > К_кр. или К_набл. < - К_кр., то нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁.

Алгоритм проверки статистических гипотез сводится к следующему:

1. Сформулировать нулевую Н₀ и альтернативную Н₁ гипотезы;

2. Выбрать уровень значимости a;

3. В соответствии с видом выдвигаемой нулевой гипотезы Н₀ выбрать статистический критерий для ее проверки, т.е. - специально подобранную случайную величину К, точное или приближенное распределение которой заранее известно;

4. По таблицам распределения случайной величины К, выбранной в качестве статистического критерия, найти его критическое значение К_кр. (критическую точку или точки);

5. На основании выборочных данных по специальному алгоритму вычислить наблюдаемое значение критерия К_набл.;

6. По виду конкурирующей гипотезы Н₁ определить тип критической области;

7. Определить, в какую область (допустимых значений или критическую) попадает наблюдаемое значение критерия К_набл., и в зависимости от этого - принять решение относительно нулевой гипотезы Н₀.

Следует заметить, что даже в том случае, если нулевую гипотезу Н₀ нельзя отклонить, это не означает, что высказанное предположение о генеральной совокупности является единственно подходящим: просто ему не противоречат имеющиеся выборочные данные, однако таким же свойством наряду с высказанной могут обладать и другие гипотезы.

Можно интерпретировать результаты проверки нулевой гипотезы следующим образом:

- если в результате проверки нулевую гипотезу Н₀ нельзя отклонить, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью отклонить нулевую гипотезу Н₀, вероятность нулевой гипотезы Н₀ больше α, а конкурирующей Н₁ - меньше 1 - α;

- если в результате проверки нулевая гипотеза Н₀ отклоняется в пользу конкурирующей Н₁, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью принять нулевую гипотезу Н₀, вероятность нулевой гипотезы Н₀ меньше α, а конкурирующей Н₁ - больше 1 - α.

В справочной таблице приведены критерии проверки гипотез.

Date: 2015-05-08; view: 770; Нарушение авторских прав