Представление результатов однократных измерений

Часто для практических целей достаточно произвести однократное измерение интересующей величины. В этом случае невозможно оценить погрешность, связанную со всеми случайными факторами «внешней среды», но мы должны быть уверены, что она достаточно мала. Чтобы убедиться в этом, необходимо хотя бы раз произвести многократное измерение величины и определить случайную погрешность. Но в любом случае остаются погрешности, связанные с использованием для измерения конкретных приборов.

Поэтому результат однократного измерения представ-ляется в виде: x ± δ x, где x – значение величины, полученное в процессе однократного прямого или косвенного измерения; δ x – погрешность однократного измерения.

Количество измерений(одно) и доверительная вероят-ность P ( 100 %) в этом случае не указываются, в отличие от результата многократного измерения.

Величина δx в случае однократного прямого измерения представляет собой приборную погрешность (см. п. 1.3).

Возникает закономерный вопрос об определении погреш-ностикосвенного измерения в этой ситуации. Перед тем как дать общий рецепт, рассмотрим достаточно простой частный случай такого определения.

Пусть стоит задача измерения объёма куба. Самый простой способ решения задачи связан с измерением L – длины ребра куба. После того как она определена, величина объёма куба рассчитывается по формуле V = L ³.

Если измерение L производилось однократно с помощью линейки, то результат такого прямого измерения представля-ется так: L ± δ L, где L – значение длины ребра, полученное в процессе однократного измерения; δ L – погрешность прямого измерения, равная погрешности линейки.

Логично потребовать, чтобы результат косвенного измерения объёма имел вид: V ± δ V.

Значение объёма V рассчитывается по формуле, связывающей его со значением длины ребра L. Остаётся определить величину δ V – погрешность для косвенного измерения объёма. Очевидно, эта величина каким-то образом должна быть связана с величиной δ L. Чтобы обнаружить эту связь, нам придётся снова обратиться к процедуре многократного измерения, но результат, который мы при этом получим, будет справедлив и для однократных измерений.

Пусть в процессе многократных измерений мы получили для одного и того же куба множество значений величины L, измеренной прямым способом, и соответствующее множество величины V, рассчитанной по формуле. Каждому значению L _i первого множества соответствует вполне определенное значение V_i второго множества. На рис. 3 представлен график зависимости V = L ³, на котором изображены точки, соответствующие результатам многократных измерений, произведённых для одного и того же куба (разброс значений очень сильно преувеличен). На оси L выделен интервал Δ L, характеризующий разброс значений длины ребра, полученный в процессе многократных прямых измерений. На оси V выделен соответствующий интервал Δ V, характеризующий разброс значений объёма, полученный в процессе вычислений. Эти интервалы определяют погрешности измерений величин L и V. Будем считать, что Δ L и Δ V достаточно малые величины по сравнению со значениями L и V. Тогда их очень просто можно связать между собой. Из треугольника (см. рис.3) следует Δ V =
= tg (α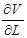) Δ L = Δ L.

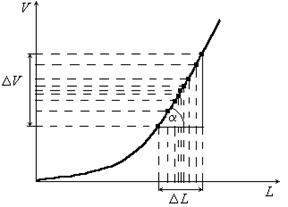Рис. 3. Экспериментальные точки на графике зависимости объёма

куба от длины его ребра (разброс значений сильно преувеличен)

Очевидно, для однократного измерения роль Δ L играет погрешность линейки δ L, а роль Δ V – интересующая нас величина δ V. Поэтому в случае однократного измерения получаем:

δ V = tg(α) δ 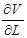L = d L,

где значение производной 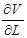= 3 L ² определяется при значении L, полученном в результате однократного прямого измерения.

Мы получили связь погрешностей прямого и косвенного измерения для частного случая. Обобщим результат на произвольную ситуацию. Пусть величина y определяется из косвенных измерений (см. п. 1.1) и является функцией нескольких независимых величин (независимых переменных), которые в свою очередь измерены либо прямо, либо косвенно. В качестве таких «переменных» могут, в частности, выступать и константы, значения которых определяются и используются при вычислениях с определённой точностью, следовательно, сами константы, так же как и другие величины, характеризуются погрешностью.

Обозначим независимые величины x ₁,..., x _n, и соответствующие им погрешности - δ x ₁,..., δ x _n. Явный вид функции y = f (x ₁,..., x _n) должен быть известен. Будем считать, что каждая величина x _i вносит свой независимый вклад в погрешность величины y. В таком случае погрешность δ y определяется следующим образом:

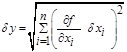(7)

В качестве примера рассмотрим определение погрешности для косвенного измерения скорости. Пусть с помощью рулетки мы произвели однократное измерение расстояния x, пройденного телом в метрах, а с помощью секундомера – затраченное на это время t в секундах. Погрешность δ x в этом случае представляет собой приборную погрешность линейки и является известной величиной. Погрешность δ t является приборной погрешностью секундомера. Значение скорости определяется по формуле v = x / t, поэтому скорость является функцией двух величин. В соответствии с общей формулой (7), определяем выражение для расчёта погрешности скорости:

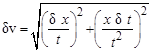. (8)

Результаты однократных измерений всех трёх величин теперь могут быть представлены в стандартной форме (без указания количества измерений и величины доверительной вероятности):

прямые измерения: (x ± δ x) м,

(t ± δ t) с,

косвенное измерение: (v ± δ v) м/с.

Величины δ x и δ v представляют собой приборные погрешности линейки и секундомера, а величина δ v, оказывается связанной с ними определённым соотношением (8).

Date: 2015-05-08; view: 1284; Нарушение авторских прав