Циклическая поляризация

Одним из видов поляризации света является циклическая поляризация – вращение плоскости колебаний линейно-поляризованной световой волны при её прохождении через некоторую специальную среду.

Способностью поворачивать плоскость поляризации проходящего света (естественной оптической активностью) обладают очень многие тела: двулучепреломляющие кристаллы (например, кварц), отдельные оптические изотропные кристаллы кубической симметрии (NaClO₃, NaBrO₃), некоторые чистые жидкости (скипидар, никотин) и их пары, растворы (широко известный пример – водный раствор сахара). Особенно много активных веществ в ряду органических соединений.

Аморфные вещества, оптически активные в твердом состоянии, сохраняют это свойство в расплавленном виде или растворе. С другой стороны, некоторые вещества, будучи неактивными в аморфном состоянии, становятся активными в кристаллическом. Например, плавленый кварц не активен, в то время как кристаллический кварц обладает значительной вращательной способностью. Следовательно, причины оптической активности скрыты как в особенностях строения молекул, так и в расположении частиц в кристаллической решетке.

Явление вращения плоскости поляризации указывает на определенную дисимметрию, свойственную оптически активным средам. Она выражается в физической неэквивалентности направления вращения по и против часовой стрелки. Многие активные вещества существуют в двух модификациях, характеризующихся равными по абсолютной величине, но противоположными по знаку удельными вращениями плоскости поляризации. Это связано у анизотропных кристаллов с зеркальной симметрией кристаллической решетки, а у жидкостей и кристаллов кубической системы – с дисимметрией молекул. Дисимметричные молекулы существуют в виде двух форм – правой и левой. Если жидкость содержит молекулы одного сорта (например, левые), то все они вращают плоскость поляризации в одну и ту же сторону (хотя, вообще говоря, в разной степени – в зависимости от ориентации молекулы). Напомним, что для оптически активных сред вращение плоскости поляризации называется правым или положительным, если плоскость поляризации световых волн для наблюдателя, смотрящего навстречу проходящему лучу, поворачивается по часовой стрелке.

В неживой природе активные вещества встречаются только в виде рацематов (т.е. содержат равные количества право- и левовращающих молекул). Такое состояние наиболее вероятно, оно обладает максимальной энтропией. В обычных реакциях химического синтеза тоже всегда получается рацематическая смесь. Совершенно иная картина в живой природе. Важнейшие биологические вещества – аминокислоты, белки, нуклеиновые кислоты, углеводы – присутствуют в виде чистых дисимметричных форм. Это свойство живого открыто уже давно; оно, несомненно, имеет огромное общебиологическое значение. В нем проявляется отклонение энтропии данной системы от максимально возможного значения. И это отличительное свойство живых организмов является одним из проявлений упорядоченности живой материи.

При помощи устройства, изображенного на рисунке 17, Араго обнаружил вращение плоскости поляризации света, так называемое явление оптической активности.

Если между скрещенными николями N ₁ и N ₂ поместить пластинку кварца, оптическая ось которой параллельна падающему лучу, то анализатор не должен пропустить свет, и поле наблюдения должно быть темным. Однако на опыте поле наблюдения оказалось просветленным. И только при повороте анализатора N ₂ на угол α удалось добиться полного затемнения поля. Это, очевидно, означает, что при прохождении света через кварцевую пластину плоскость поляризации, т.е. плоскость колебаний электрического вектора Е, поворачивается на определенный угол α, причем свет все время остается линейно поляризованным.

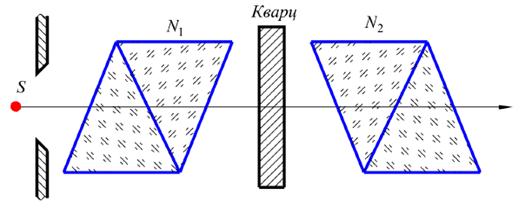
Рисунок 17 – Прохождение пучка света последовательно через две призмы Николя и кристаллическую пластинку, помещённую между ними

Наблюдения оптической активности в кварце показали, что существует две модификации кварца: правовращающий, или положительный, дающий поворот электрического вектора по часовой стрелке, и левовращающий, или отрицательный (вращение против часовой стрелки). При этом величина вращения в обоих случаях при прочих равных условиях одинакова. По-видимому, и другие оптически активные кристаллы существуют в двух модификациях, хотя не во всех случаях их удалось обнаружить.

Вращение плоскости поляризации наблюдается также и в некристаллических телах. К ним принадлежат, например, скипидары, метиловые эфиры жирных кислот, растворы сахара, камфары и т.д. Это означает, что данное явление не связано с анизотропией в противоположность двойному лучепреломлению. В настоящее время известны тысячи активных веществ, обладающих различной вращающейся способностью.

Стоит отметить, что угол поворота α зависит не только от природы вещества, через который проходит линейно-поляризованный свет, но и от длины волны света. Данная зависимость называется вращательной дисперсией (зависимость угла поворота плоскости поляризации от длины волны). Особенность вращательной дисперсии состоит в том, что она намного больше, чем дисперсия показателя преломления. В первом приближении угол α обратно пропорционален квадрату длины волны (α = A / λ ²). Почти в три раза изменяется угол a при переходе от красного края спектра к фиолетовому. Кварцевая пластина толщиной в 1 мм производит следующие вращения: 12,65° (λ = 759,4 нм); 21,72° (λ = 589,3 нм); 42,59° (λ = 430,8 нм).

Теория циклической поляризации (теория Френеля)

Теория вращения плоскости поляризации пучка света впервые была дана Френелем. Френель основывался на предположении, что оптически активные вещества обладают особым типом двойного лучепреломления, заключающимся в разложении линейно поляризованного светового колебания на два колебания, поляризованных по правому и левому кругу. При этом лучи, поляризованные по правому и левому кругу, имеют различные скорости распространения v_п и v_л.

Показатели преломления для таких лучей будут различны

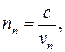
	(30)
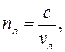
	(31)

где c – скорость света в вакууме. При прохождении среды толщиной l между лучами возникает разность хода

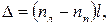
(32)

и соответствующая разность фаз

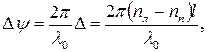
(33)

где λ ₀ – длина световой волны в вакууме.

Свяжем разность фаз Δ ψ с углом поворота вектора поляризации. Для этого воспользуемся тем фактом, что любое линейно поляризованное колебание (на рисунке 18, а – колебание вдоль оси 0 X)

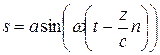
(34)

может быть разложено в любой точке пространства z на два колебания, поляризованных по левому и правому кругу с амплитудами a /2 и равными фазами

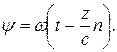
(35)

Для циркулярно поляризованных колебаний фаза имеет смысл углов поворота векторов 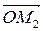и 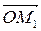, соответственно, против часовой стрелки и по часовой стрелки. Действительно, как видно из рисунков 18, а, 18, б и 18, в, в любой момент времени t суммарный вектор

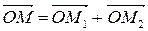
(36)

представляет собой колебание, направленное вдоль прямой 0 X.

В результате распространения циркулярно поляризованных колебаний в активной среде фазы этих колебаний (углы поворота) становятся неодинаковыми из-за различия показателей преломления n_л и n_п. Поэтому на выходе из активной среды толщиной l углы поворота векторов 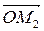и 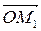будут различаться на величину разности фаз:

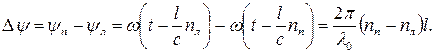
(37)

Предположим для определенности, что показатель преломления для левого колебания больше показателя преломления для правого колебания. Это означает, как видно из выражения (37) для фазы, что угол поворота левого колебания меньше угла поворота правого колебания. Тогда на выходе из активной среды результирующее линейно поляризованное колебание 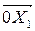(сумма 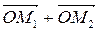) оказывается повернутым по часовой стрелке по отношению к первоначальному направлению 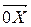на угол α. Вычислим этот угол. Из рисунка видно, что 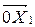, будучи биссектрисой угла M ₁0 M ₂, составляет с направлением 0 М ₁ угол

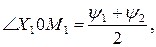
(38)

откуда для угла α получаем

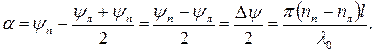
(39)

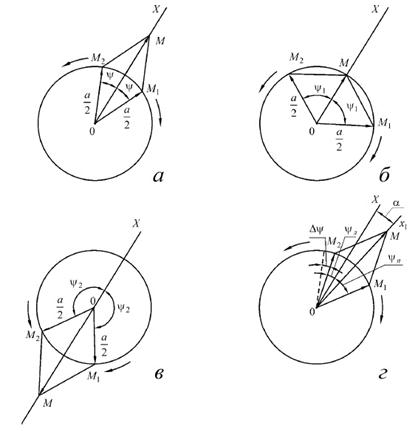
Рисунок 18 – Разложение линейно поляризованной волны на циркулярно поляризованные волны, распространяющиеся с одинаковыми скоростями в неактивной среде (а, б, в) и различными скоростями в активной среде (г)

Date: 2015-05-08; view: 2235; Нарушение авторских прав