
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вводная часть. При рассмотрении неравновесных процессов, протекающих при движениисплошнойсреды, в подвижной среде выделяется элемент потока (макрочастица
|
|
При рассмотрении неравновесных процессов, протекающих при движениисплошнойсреды, в подвижной среде выделяется элемент потока (макрочастица, или жидкая частица). Объём макрочастицы должен быть, с одном стороны, элементарным, чтобы в пределах его можно было пренебречь изменением термодинамических параметров и считать состояние макрочастицы равновесным, а с другой стороны, он должен быть достаточно большим, чтобы число содержащихся в нём молекул было достаточно для статистического осреднения их кинетических энергий и однозначного определения макроскопических величин.
Элемент потока при движении деформируетсяи изменяет свой объём, но масса его остается неизменной, т. е. рассматривается подвижная закрытая равновесная термодинамическая система, состояние которой однозначно определяется параметрами 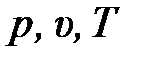 . Изучаемое течение среды (поток) рассматривается как движение совокупности непрерывно распределённых в пространстве элементов среды (жидких частиц).
. Изучаемое течение среды (поток) рассматривается как движение совокупности непрерывно распределённых в пространстве элементов среды (жидких частиц).
Абсолютное движение микрочастиц (атомов, молекул), составляющих элемент потока, относительно неподвижных стенок канала можно представить как сумму двух движений: хаотического (теплового) – относительного движения относительно центра инерции элемента потока и направленного механического(переносного) движения вместе с центром инерции (полюсом) относительно стенок канала. Для каждого вида движения микрочастиц составляется соответствующее балансовое уравнение изменения энергии:
1) для хаотического движения микрочастиц относительно их центра инерции – уравнение первого закона термодинамики для хаотического движения (2.42)
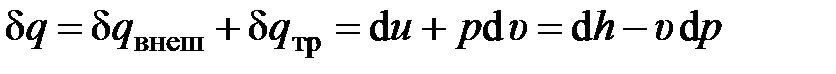 ; (2.63)
; (2.63)
2) для направленного движения микрочастиц относительно стенок канала – уравнение энергии для потока в механическом виде (для направленного движения) – обобщённое уравнение Бернулли для стационарного течения
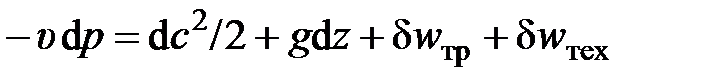 ; (2.64)
; (2.64)
3) для абсолютного движения микрочастиц относительно стенок канала – уравнение первого закона термодинамики для стационарного потока
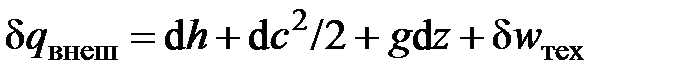 , (2.65)
, (2.65)
где h – удельная энтальпия, Дж/кг.
Течение газа без внешнего теплообмена (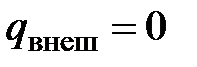 ) и совершения технической работы называется энергоизолированным. Такое течение происходит в различных каналах (соплах, диффузорах).
) и совершения технической работы называется энергоизолированным. Такое течение происходит в различных каналах (соплах, диффузорах).
Интегрируя (2.64) в случае энергоизолированного течения вязкой
несжимаемой жидкости (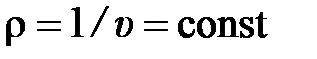 ), получим известное в гидромеханике уравнение Бернулли виде баланса напоров
), получим известное в гидромеханике уравнение Бернулли виде баланса напоров
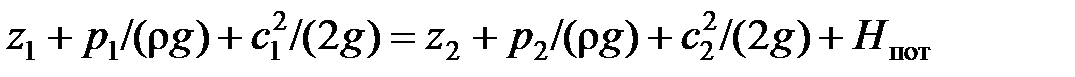
или баланса давлений
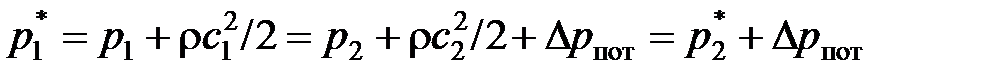 . (2.66)
. (2.66)
Особенности адиабатного течения газа. Процесс, протекающий без внешнего теплообмена, называется адиабатным. Следует различать адиабатный процесс с трением – реальный адиабатный процесс (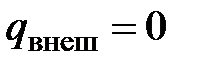 ,
, 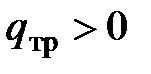 ), протекающий с изменением энтропии (
), протекающий с изменением энтропии (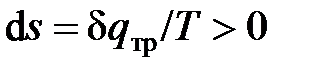 ) и описываемый уравнением политропы
) и описываемый уравнением политропы  или уравнением реальной адиабаты
или уравнением реальной адиабаты 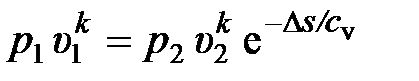 , и адиабатный процесс без трения – теоретический (идеальный, обратимый, равновесный) адиабатный процесс или изоэнтропный (без внешнего и внутреннего теплообмена), протекающий без изменения энтропии
, и адиабатный процесс без трения – теоретический (идеальный, обратимый, равновесный) адиабатный процесс или изоэнтропный (без внешнего и внутреннего теплообмена), протекающий без изменения энтропии  и описываемый уравнением идеальной адиабаты или изоэнтропы
и описываемый уравнением идеальной адиабаты или изоэнтропы
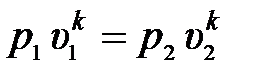 . (2.67)
. (2.67)
Уравнение первого закона термодинамики для стационарного потока (2.65) в случае энергоизолированного изоэнтропного (без трения) течения газа (изменением гравитационной потенциальной энергии газа в канале обычно пренебрегают 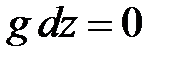 ) запишется в интегральном виде:
) запишется в интегральном виде:
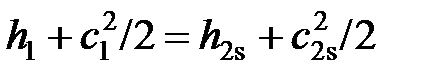 , (2.68)
, (2.68)
где индекс «s» указывает, что процесс изоэнтропный ( ).
).
При течении с трением кинетическая энергия элемента среды уменьшается, а энтальпия увеличивается, но баланс этих величин сохраняется в прежнем виде
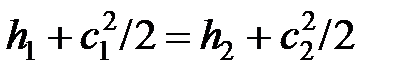 . (2.69)
. (2.69)
Таким образом, уравнения первого закона термодинамики для течения с трением (2.69) и без трения (2.68) имеют одинаковый вид и, если опустить индекс «s» (что часто и делают), то они ничем не будут отличаться по внешнему виду. Различие этих уравнений состоит лишь в соотношении между энтальпией и кинетической энергией для течений с трением и без трения. Эти уравнения являются основными в газовой динамике при рассмотрении энергоизолированных течений сжимаемых газов и паров в каналах.
При течении идеального газа энтальпия зависит только от температуры и её можно выразить так
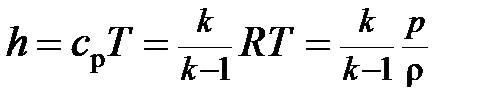 . (2.70)
. (2.70)
С учётом (2.70) уравнения (2.68) и (2.69) примут вид
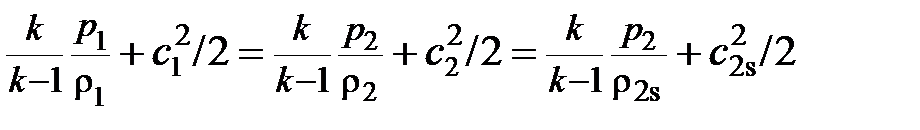 . (2.71)
. (2.71)
Это уравнение играет ту же роль для сжимаемого газа, что и уравнение Бернулли (2.66) для несжимаемого газа.
При истечении газа из ресивера (сосуда большого объёма) кинетическая энергия элемента потока в начале разгона мала и ею можно пренебречь 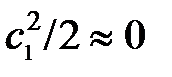 . Тогда уравнение (2.69) примет вид
. Тогда уравнение (2.69) примет вид 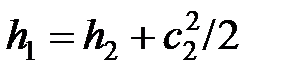 . Из этого уравнения определяется скорость потока по значениям энтальпий в ресивере
. Из этого уравнения определяется скорость потока по значениям энтальпий в ресивере 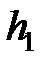 и на выходе из сопла
и на выходе из сопла 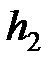 (рис. 16)
(рис. 16)
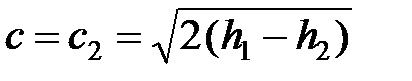 . (2.72)
. (2.72)
Это уравнение применяется для расчёта скорости истечения реальных газов (паров).

а) – схема течения газа в сопле; б) – зависимость параметров потока на выходе из сопла от отношения 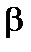 Рисунок 16 – К расчёту истечения газа из сопла
Рисунок 16 – К расчёту истечения газа из сопла
|
При истечении идеальных газов формула (2.72) с учётом (2.70) принимает вид
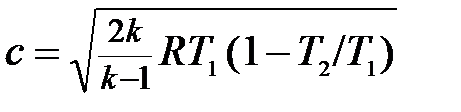 . (2.73)
. (2.73)
Выражения (2.72) и (2.73) могут применяться для расчёта скорости истечения как с трением, так и без трения. В случае истечения без трения (изоэнтропное течение) отношение температур можно представить в виде отношения давлений по уравнению изоэнтропы
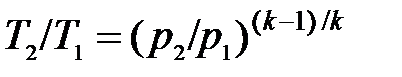 (2.74)
(2.74)
и для расчёта теоретической скорости в сопле из (2.73) получается формула
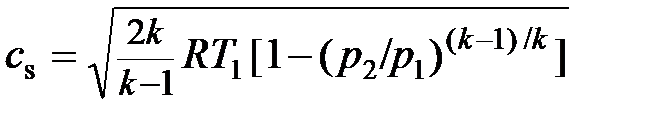 . (2.75)
. (2.75)
Теоретический массовый расход определяется по формуле
 , (2.76)
, (2.76)
где А - площадь проходного сечения на выходе из сопла.
Плотность в выходном сечении сопла определяется из уравнения изоэнтропы (в случае течения с трением это уравнение не справедливо)
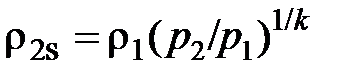 . (2.77)
. (2.77)
Если выражения для скорости (2.75) и для плотности (2.77) подставить в (2.76), то получим формулу для расчета теоретического массового расхода (кг/с)
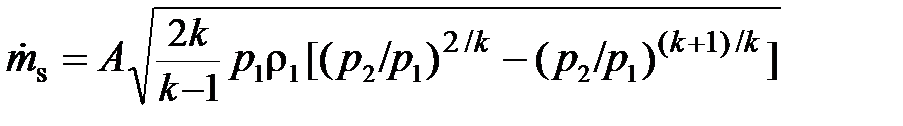 . (2.78)
. (2.78)
Отношение давления окружающей среды, в которую происходит истечение, к давлению в ресивере принято обозначать
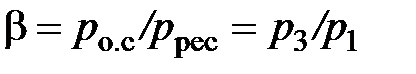 (2.79)
(2.79)
и в функции от этой величины анализировать скорость и расход.
Опыт показывает, что по мере понижения давления в окружающей среде при постоянном давлении в ресивере (по мере уменьшения  ) давление на выходе из сопла также понижается и равняется давлению в окружающей среде
) давление на выходе из сопла также понижается и равняется давлению в окружающей среде 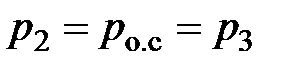 , одновременно растёт скорость истечения и расход газа (см. рисунок 16). Однако при достижении определённого соотношения между давлением в ресивере и окружающей среде расход и скорость истечения достигают максимального значения и при дальнейшем понижении
, одновременно растёт скорость истечения и расход газа (см. рисунок 16). Однако при достижении определённого соотношения между давлением в ресивере и окружающей среде расход и скорость истечения достигают максимального значения и при дальнейшем понижении 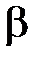 параметры на выходе из сопла становятся постоянными (в этом случае говорят, что происходит «запирание сопла»).
параметры на выходе из сопла становятся постоянными (в этом случае говорят, что происходит «запирание сопла»).
Отношение давлений 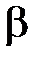 , при котором происходит запирание сопла, называется критическим. Критическое отношение давлений может быть определено, если исследовать уравнение расхода (2.78) на максимум,
, при котором происходит запирание сопла, называется критическим. Критическое отношение давлений может быть определено, если исследовать уравнение расхода (2.78) на максимум,
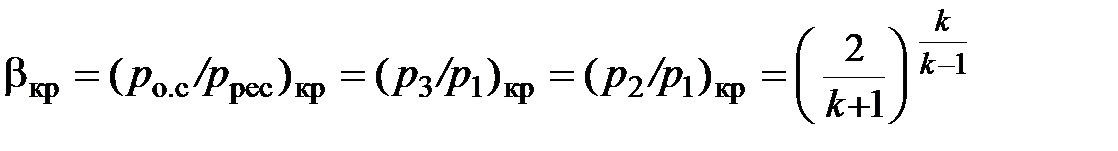 . (2.80)
. (2.80)
Для воздуха k = 1,40 и 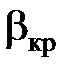 = 0,528.
= 0,528.
При критическом истечении скорость на выходе из сопла становится равной местной скорости звука в потоке (т. е. скорости звука, определяемой параметрами газа в данном сечении сопла). Скорость звука зависит с температуры и определяется по формуле
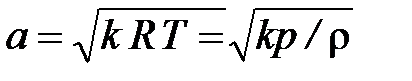 . (2.81)
. (2.81)
Если в (2.75) подставить (2.80), то получим выражение для расчёта критическое скорости истечения (для воздуха R = 287 Дж/(кг.К))
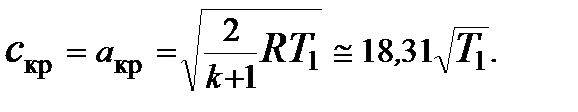 (2.82)
(2.82)
При критическом режиме истечения расход газа достигает максимума и остаётся постоянным, несмотря на дальнейшее понижение давления в окружающей среде,
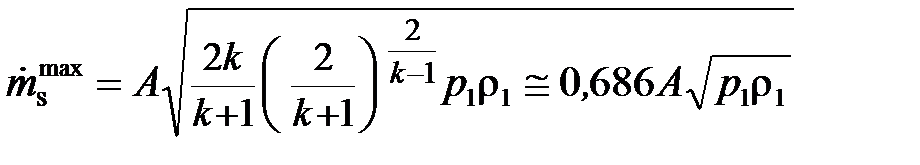 . (2.83)
. (2.83)
Для расчета действительной скорости истечения и действительного расхода надо знать коэффициенты скорости и расхода, которые определяются опытным путём и зависят от конструкции сопла и чистоты его поверхности.
Отношение действительной скорости истечения к теоретической называется коэффициентом скорости или скоростным коэффициентом
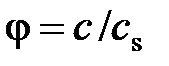 . (2.84)
. (2.84)
Отношение действительного расхода к теоретическому называется коэффициентом расхода
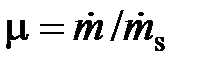 (2.85)
(2.85)
Возникновение критического истечения можно пояснить так. Если считать давление 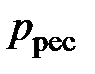 неизменным, то уменьшение давления
неизменным, то уменьшение давления 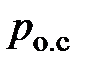 приводит к перераспределению давления вдоль сопла, при этом в выходном сечении устанавливается давление
приводит к перераспределению давления вдоль сопла, при этом в выходном сечении устанавливается давление 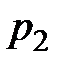 . Оно равно давлению
. Оно равно давлению  до тех пор, пока скорость потока газа в выходном сечении не достигнет критического значения, т. е. не станет равной местной скорости звука. Дальнейшее уменьшение давления
до тех пор, пока скорость потока газа в выходном сечении не достигнет критического значения, т. е. не станет равной местной скорости звука. Дальнейшее уменьшение давления  уже не будет сказываться на перераспределении давлений в сопле, т. к. внешние возмущения (изменения давления), распространяющиеся со скоростью звука относительно потока, не могут проникнуть внутрь сопла; таким образом давление в выходном сечении сопла остаётся неизменным, равным критическому
уже не будет сказываться на перераспределении давлений в сопле, т. к. внешние возмущения (изменения давления), распространяющиеся со скоростью звука относительно потока, не могут проникнуть внутрь сопла; таким образом давление в выходном сечении сопла остаётся неизменным, равным критическому 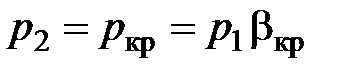 .
.

| 1 – вакуумный насос; 2 – труба; 3 – мерная шайба; 4 – U-образный манометр; 5 – сопло; 6 и 7 – вакуумметры; 8 – вентиль; 9 – сеточка; 10 – барометр; 11 – термометр Рисунок 17 – Схема установки для исследования истечения воздуха из сопла |
Описание лабораторной установки. Установка (рисунок 17) состоит из вакуумного насоса 1 производительностью 20 л/с, трубы 2 диаметром 25 мм и длиной 1000 мм, мерной шайбы 3 и
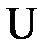 -образного манометра 4 для измерения действительного расхода воздуха через сопло, сопла 5 диаметром
-образного манометра 4 для измерения действительного расхода воздуха через сопло, сопла 5 диаметром 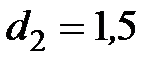 мм на выходе, вакуумметров 6 и 7, служащих для определения разрежения в выходном сечении сопла и в пространстве за соплом – окружающей среде. Разрежение в окружающей среде, а значит и в сопле, регулируется вентилем 8. Сеточка 9 предохраняет насос и сопло от попадания различных частиц. Для измерения параметров атмосферы служат барометр 10 и термометр 11.
мм на выходе, вакуумметров 6 и 7, служащих для определения разрежения в выходном сечении сопла и в пространстве за соплом – окружающей среде. Разрежение в окружающей среде, а значит и в сопле, регулируется вентилем 8. Сеточка 9 предохраняет насос и сопло от попадания различных частиц. Для измерения параметров атмосферы служат барометр 10 и термометр 11. Поскольку скорость воздуха в трубе перед соплом мала (менее 0,5 м/с), то значения параметров воздуха перед соплом близки значениям параметров атмосферного воздуха в лаборатории:
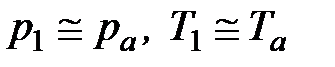 .
.Date: 2015-05-08; view: 1081; Нарушение авторских прав