Вводная часть. Виды теплоёмкостей. Согласно первому закону термодинамики

Виды теплоёмкостей. Согласно первому закону термодинамики

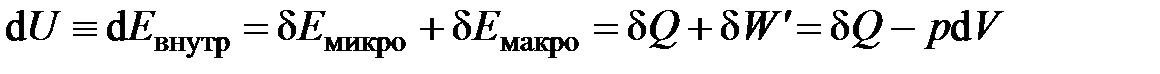
или для удельных величин

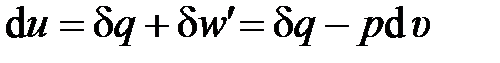(2.42)

изменение внутренней энергии системы по способу подвода движения и расчета его энергии разбивается на две части (составляющие):

– работу – энергию движения, подводимого (отводимого) к системе макроскопическим путем (та часть изменение внутренней энергии, которая рассчитывается через макроскопические силы и перемещения) и

– теплоту – энергию движения, подведённого (отведенного) к системе микроскопическим путём (та часть изменения внутренней энергии, которая в общем случае не рассчитывается через силы и перемещения).

Возникает вопрос, как же рассчитать теплоту 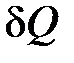, если её в общем случае не удаётся рассчитать через силы и перемещения (в отдельных случаях теплоту можно рассчитать так же, как и работу через силы и перемещения, например при трении).

Из опыта известно, что при подводе тепла, как правило, растёт температура рабочего тела. Поэтому количество подведённого к телу тепла исторически определяли как величину, пропорциональную изменению температуры тела: 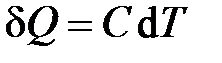. Коэффициент пропорциональности , позволяющий установить связь между теплотой и изменением температуры тела, называется теплоёмкостью тела. Таким образом, теплоёмкость тела определяется как физическая величина, равная отношению теплоты к изменению температуры тела

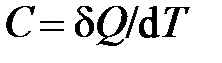, [ ] = 1 Дж/К.

Теплоемкость тела численно равна теплоте, вызывающей изменение температуры тела на один градус.

Следует заметить, что и при свершении работы изменяется температура тела. Поэтому и работу можно рассчитывать пропорционально изменению температуры: 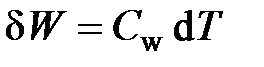, где 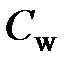можно назвать «работоемкость», для которой создать специальные таблицы. Однако этого не требуется, т. к. работу гораздо проще рассчитать через силы и перемещения. Следовательно, введение двух физических величин – теплоты и работы – при рассмотрении первого закона термодинамики обусловлено, в первую очередь, различными методами их расчёта.

В теплотехнических расчётах вместо теплоёмкости тела широко используются удельная, объёмная и молярная теплоёмкости.

Удельной теплоёмкостью называется отношение теплоёмкости тела к его массе

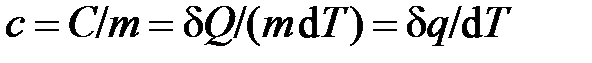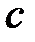, [ ] = 1 Дж/(кг×К),

где 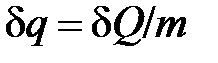– удельная теплота, Дж/кг (неправильно называть удельную теплоёмкость массовой теплоёмкостью, см. приложение Б).

Молярной теплоёмкостью называется отношение теплоёмкости тела к количеству вещества (молярности) этого тела:

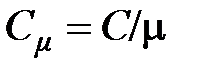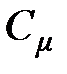, [ ] = 1 Дж / (моль×К).

Объёмной теплоёмкостью называется отношение теплоёмкости тела к его объёму, приведённому к нормальным физическим условиям (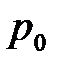 = 101325 Па = 760 мм рт. ст.; 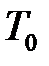= 273, 15 К (0 ^оС)):

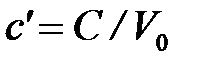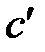, [ ] = 1 Дж/(м ³×К).

В случае идеального газа его объём при нормальных физических условиях (НФУ) вычисляется из уравнения состояния

.

Связь между различными видами теплоёмкости:

; ,

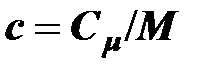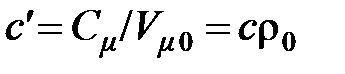где 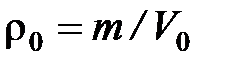– плотность газа при НФУ,

= 22,4141 м³/кмоль – молярный объём, приведённый к НФУ.

Теплоёмкость идеального газа зависитот температуры 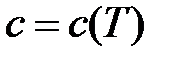. По этому признаку различают истинную и среднюю теплоёмкости.

Истинная теплоёмкость соответствует определённой температуре тела (теплоёмкость в точке), так как определяется при бесконечно малом изменении температуры тела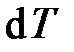

.

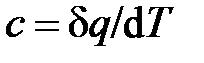Значение теплоёмкости, которое принимается постоянным в заданном интервале температур от 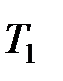до 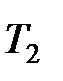, называется средней теплоёмкостью в данном интервале температур. Она определяется как отношение теплоты к конечному интервалу температур

.

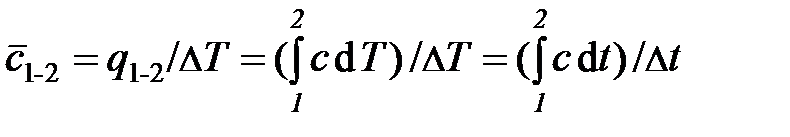Согласно первому закону термодинамики (2.42) одному и тому же изменению внутренней энергии соответствует бесчисленное множество сочетаний различных значений теплоты и работы, т. е. при одном и том же изменении температуры (внутренней энергии) тела теплота, а значит и теплоёмкость, будут различными в различных термодинамических процессах.

В случае изотермного процесса (Т = const) температура тела не изменяется (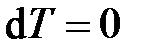 и ) и 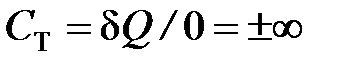теплоту уже нельзя определить как величину, пропорциональную изменению температуры. В этом случае она определяется из первого закона термодинамики, как работа изменения объёма (d U = 0): .

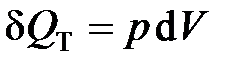В случае изобарного процесса (р = const) уравнение первого закона термодинамики (2.42) запишется в виде

.

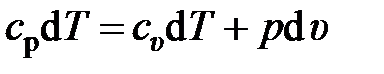Откуда выводится известное уравнение Майера

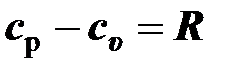, (2.43)

согласно которому разность удельной изобарной и изохорной теплоёмкостей для данного газа есть величина постоянная и равная удельной газовой постоянной.

В случае адиабатного процесса теплота равна нулю (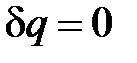), а значит и теплоёмкость равна нулю: .

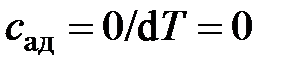Уравнение первого закона термодинамики в этом случае запишется в виде

.

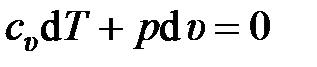Откуда выводится уравнение адиабатного процесса (адиабаты)

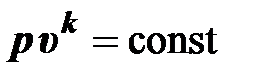. (2.44)

Показатель степени, входящий в это уравнение и равный отношению теплоёмкостей, называется показателем адиабаты :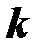

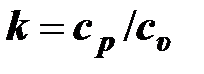. (2.45)

Решая совместно (2.43) и (2.45), можно выразить теплоёмкости через 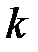и :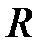

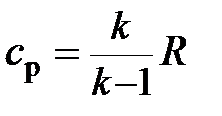; (2.46)

Значения истинных теплоёмкостей и их отношения 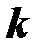некоторых газов в идеальном состоянии (при 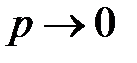и T _C = 0 ^оС) приведены в таблице 7.

ъ

Таблица 7 – Некоторые характеристики идеальных газов

Газ	Химическая формула
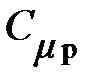
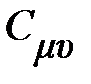
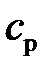
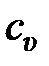
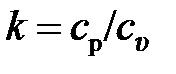
кг/кмоль	кДж/(кмоль×К)	кДж/(кг×К)
Гелий	He	4,0026	20,93	12,60	5,229	3,148	1,661
Водород	H2	2,0158	28,58	20,270	14,180	10,056	1,410
Метан	CH4	16,0426	34,74	26,42	2,165	1,647	1,315
Аммиак	NH3	17,0304	35,00	26,67	2,055	1,566	1,312
Водяной пар	H2O	18,016	33,504	25,190	1,8597	1,3982	1,330
Оксид углерода	CO	28,0104	29,099	20,785	1,0389	0,7421	1,400
Азот	N2	28,0134	29,103	20,789	1,0389	0,7421	1,400
Воздух		28,9642	29,050	20,736	1,0030	0,7159	1,401
Кислород	O2	31,9988	29,224	20,910	0,9132	0,6534	1,398
Аргон	Ar	39,948	20,79	12,48	0,520	0,312	1,666
Диоксид углерода	CO2	44,0098	35,989	27,675	0,8178	0,6288	1,301
Диоксид серы	SO2	64,0588	38,85	30,52	0,607	0,476	1,273
Пары ртути	Hg	200,59	20,83	12,52	0,104	0,062	1,664

В среднем по всем газам одинаковой атомарности принято считать, что для одноатомных газов 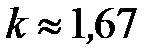, для двухатомных 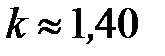, для трёхатомных 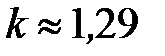(для водяных паров часто берут точное значение ).

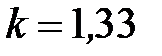В случае произвольного процесса уравнение первого закона термодинамики запишется в виде

.

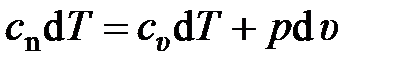Откуда по аналогии с уравнением адиабатного процесса (2.44), полученного исторически первым, выводится уравнение политропного процесса (политропы) в виде

,

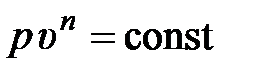где показатель степени 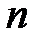, постоянный для данного процесса, называется показателем политропы

.

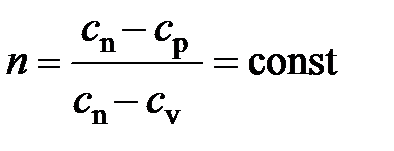Таким образом, если процесс политропный и показатель политропы 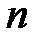известен, то теплоёмкость политропного процесса 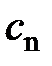этого процесса может быть определена расчётным путём, не прибегая к эксперименту, по формуле _.

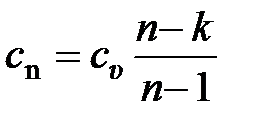Расчёт теплоты через средние теплоёмкости осуществляется по формулам:

– для изохорного процесса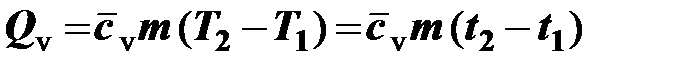

– для изобарного процесса .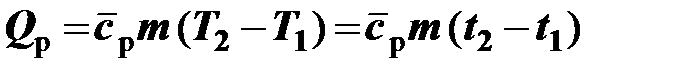

Date: 2015-05-08; view: 937; Нарушение авторских прав