Определение погрешности результатов измерений

Оценка точности результатов опыта обязательна, так как полученные значения могут лежать в пределах возможной погрешности опыта, а выведенные закономерности – оказаться неясными и даже неверными. Точность есть степень соответствия результатов измерений действительному значению измеряемой величины. Понятие точности связано с понятием погрешности: чем выше точность, тем меньше погрешность измерений, и наоборот. Самые точные приборы не могут показать действительного значения величины, их показания содержат погрешность.

Разность между действительным значением измеряемой величины 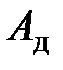и измеренным 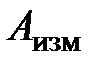называется абсолютной погрешностью измерения. Практически под абсолютной погрешностью 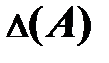понимают разность между результатом измерения при помощи более точных методов или приборов высшей точности (образцовых) и значением этой величины, полученным прибором, применяемым в исследовании:

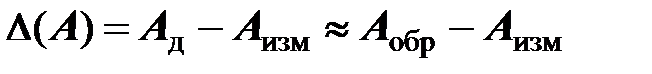. (1.7)

Абсолютная погрешность не может, однако, служить мерой точности, так как, например, 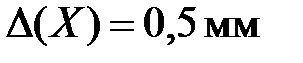при 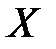= 100 мм достаточно мала, но при 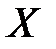= 1 мм очень велика. Поэтому для оценки точности измерений вводится понятие относительной погрешности 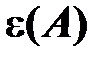, равной отношению абсолютной погрешности результата измерений к измеряемой величине

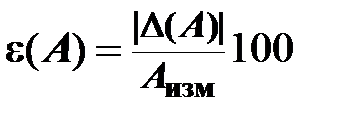. (1.8)

За меру точности измеряемой величины понимают величину, обратную 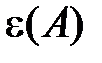. Следовательно, чем меньше относительная погрешность 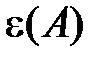, тем выше точность измерений. Например, если относительная ошибка измерений получена равной 2 %, то говорят, что измерения выполнены с погрешностью не более 2 % или с точностью не менее 0,5 %, или с точностью не менее 1/0,02 = 50. Не следует использовать термин "точность" взамен терминов "абсолютная погрешность" и "относительная погрешность". Например, неправильно говорить "масса измерена с точностью 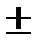0,1 мг", так как 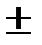0,1 мг не точность, а абсолютная погрешность измерения массы.

Различают систематические, случайные и грубые погрешности измерений.

Систематические погрешности связаны в основном с погрешностями средств измерений и остаются постоянными при повторных измерениях.

Случайные погрешности вызываются неконтролируемыми обстоятельствами, например, трением в приборах. Случайные погрешности измерений можно выразить несколькими понятиями.

Под предельной 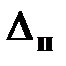(максимальной) абсолютной погрешностью понимают такое её значение, при котором вероятность попадания погрешности в интервал 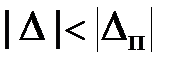настолько велика, что событие можно считать практически достоверным. При этом лишь в отдельных случаях погрешность может выйти за пределы указанного интервала. Измерение с такой погрешностью называют грубым (или промахом) и при обработке результатов исключают из рассмотрения.

Значение измеряемой величины можно представить формулой

,

что следует читать так: истинное значение измеряемой величины находится в пределах от 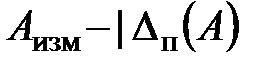до .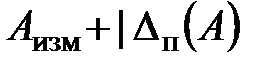

Способ обработки опытных данных зависит от характера измерений, которые могут быть прямыми и косвенными, однократными и многократными. Однократно производятся измерения величин, когда невозможно или затруднительно повторно произвести условия измерения. Обычно это имеет место при измерениях в производственных, а иногда и лабораторных условиях.

Значение измеряемой величины при однократном измерении прибором может отличаться от истинных значений не более чем на значение предельной погрешности, допускаемой классом точности прибора ,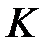

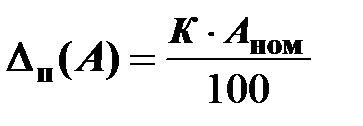. (1.9)

Как следует из соотношения (1.9), класс точности прибора выражает наибольшую допустимую погрешность 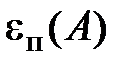в процентах от номинального значения 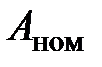(предельного) шкалы прибора. Все приборы делятна восемь классов точности: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5 и 4,0.

Необходимо помнить о том, что класс точности прибора ещё не характеризует точность измерений, получаемую при пользовании этим прибором, так как относительная погрешность измерения в начальной части шкалы больше (точность меньше), чем в конечной части шкалы при почти неизменной абсолютной погрешности. Именно наличием этого свойства показывающих приборов объясняется стремление выбирать предел измерения прибора таким образом, чтобы в процессе эксплуатации прибора отсчёт по шкале производился в области между серединой шкалы и её конечной отметкой или, говоря другими словами, во второй половине шкалы.

Пример. Пусть ваттметром на 250 Вт (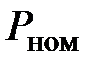 = 250 Вт) с классом точности 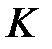= 0,5 измерена мощность 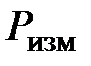= 50 Вт. Требуется определить предельную абсолютную погрешность и относительную погрешность измерения. Для этого прибора в любой части шкалы допускается абсолютная погрешность, равная 0,5 % от верхнего предела измерения, т. е. от 250 Вт, что составляет

.

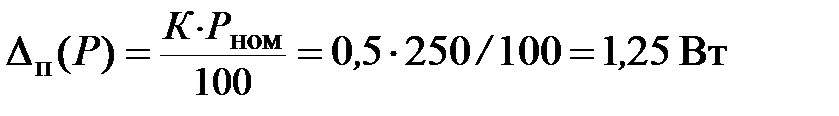Предельная относительная погрешность при измеренной мощности 50 Вт

.

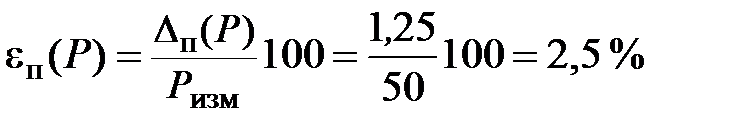Из этого примера видно, что класс точности прибора (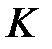 = 0,5) и предельная относительная погрешность измерения в произвольной точке шкалы прибора (в примере 2,5 % для 50 Вт) в общем случае не равны (они равны только для номинального значения шкалы прибора).

К косвенным измерениям обращаются, когда прямые измерения искомой величины 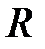неосуществимы или затруднены. Косвенные измерения сводятся к измерению независимых величин А, В, С…, связанных с искомой величиной функциональной зависимостью
.

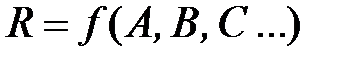Предельная относительная погрешность косвенных измерений величины равна дифференциалу её натурального логарифма, причём следует брать сумму абсолютных значений всех членов такого выражения (брать со знаком плюс):

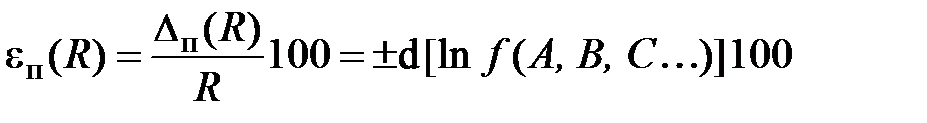(1.10)

При теплотехнических экспериментах для определения теплопроводности материала 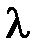, коэффициентов теплоотдачи 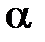и теплопередачи 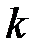прибегают к косвенным измерениям. В качестве примера рассмотрим вычисление предельной относительной погрешности при косвенном измерении теплопроводности .

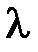Теплопроводность материала по методу цилиндрического слоя выражается уравнением

.

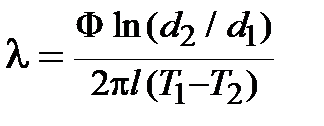Логарифм этой функции имеет вид

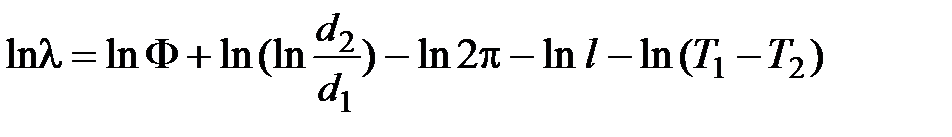
а дифференциал с учётом правила знаков (всё берётся с плюсом)

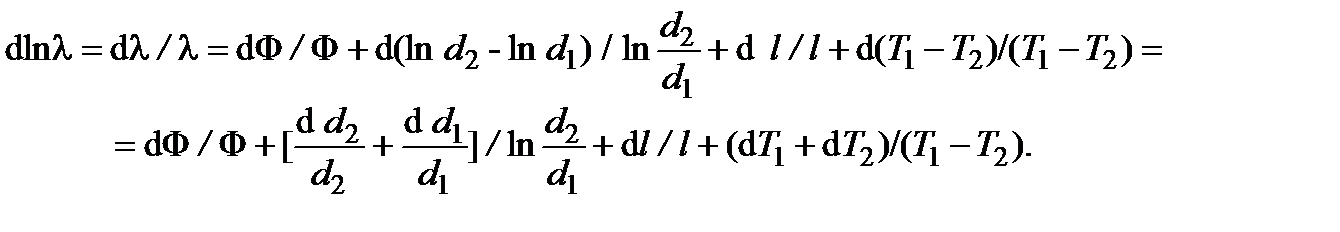
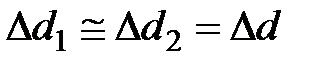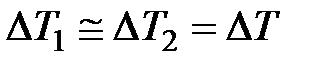Тогда относительная погрешность измерения теплопроводности материала, считая и , определится выражением

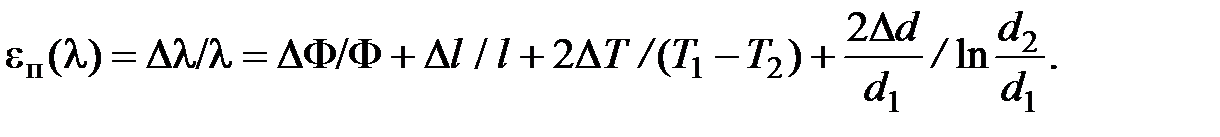(1.11)

Абсолютная погрешность измерения длины и диаметра трубы принимается равной половине цены наименьшего деления шкалы линейки или штангенциркуля, температуры 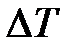и теплового потока 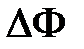– по показаниям соответствующих приборов с учётом их класса точности.

При определении значений случайных погрешностей, кроме предельной погрешности вычисляют статистическую погрешность неоднократных (нескольких) измерений. Эту погрешность устанавливают после измерений при помощи методов математической статистики и теории ошибок.

В качестве приближённого значения измеряемой величины теория ошибок рекомендует использовать среднее арифметическое :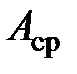

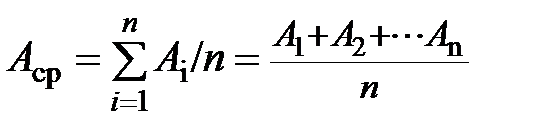, (1.12)

где 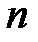– число измерений величины .

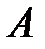Для оценки достоверности результатов измерений, принимаемых равными среднему значению 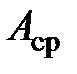, служит среднее квадратичное отклонение результата нескольких измерений (среднего арифметического)

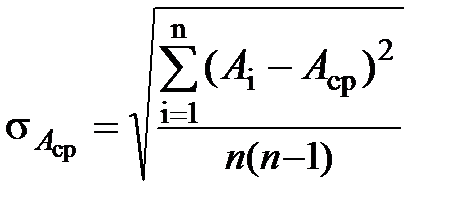. (1.13)

Среднее квадратичное отклонение отдельного измерения (или стандарт) получается больше среднего квадратичного отклонения среднего арифметического и определяется выражением

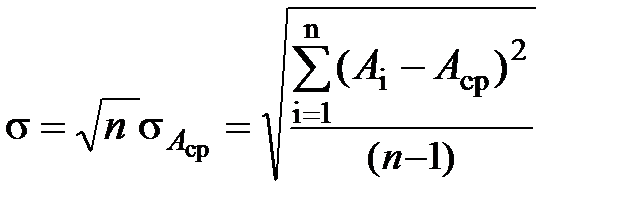. (1.14)

Статистическая погрешность среднего арифметического значения (результата измерения) при малом числе наблюдений (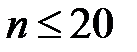) и заданной доверительной вероятности 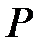определяется по формуле

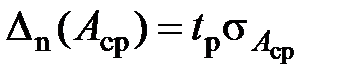. (1.15)

Значения 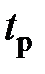для наиболее употребительного интервала доверительных вероятностей 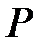и различных 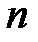приведены в таблице ПI-4-1 [11], которая основана на распределении Стьюдента. Выбор значений доверительной вероятности 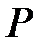зависит от вида измерений. При исследовании закономерностей в самом общем виде (без деталей), например, характера кривых развития явления, достаточна доверительная вероятность 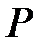= 0,68. Для измерений, связанных с конструкцией машин, вполне достаточна вероятность 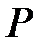= 0,90. При определении деталей закономерностей и значений величин, являющихся основой для дальнейшего расчёта, необходима доверительная вероятность
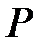= 0,99. Для доверительной вероятности 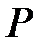= 0,99 по таблице ПI-4-1 находим для четырёх опытов 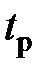= 5,84 и при пяти опытах 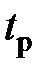= 4,6.

В практических исследованиях чаще всего пренебрегают возможностью отклонений от среднего, больших 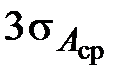(правило трёх сигм). В этом случае истинное значение результата нескольких измерений определяется выражением

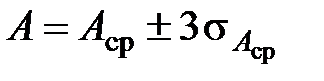. (1.16)

Date: 2015-05-08; view: 3730; Нарушение авторских прав