Как составить параметрические уравнениЯ прямой?

Параметрические уравнения прямой больше актуальны для прямых в пространстве, но без них наш конспект осиротеет.

Если известна некоторая точка 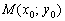, принадлежащая прямой, и направляющий вектор 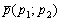этой прямой, то параметрические уравнения данной прямой задаются системой:

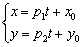
Что такое функция, заданная параметрически, я уже объяснял в статье Производная неявной и параметрически заданной функций. Но всё равно немного повторюсь в следующей демонстрационной задаче:

Пример 13

Составить параметрические уравнения прямой по точке 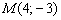и направляющему вектору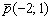

Решение закончилось, не успев начаться:

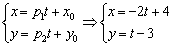
Параметр «тэ» может принимать любые значения от «минус бесконечности» до «плюс бесконечности», и каждому значению параметра соответствует конкретная точка плоскости. Например, если 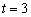, то получаем точку .

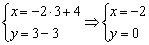Обратная задача: как проверить, будет ли точка 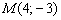условия принадлежать данной прямой?

Подставим координаты точки 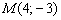в полученные параметрические уравнения:

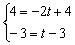
Из обоих уравнений следует, что 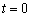, то есть, система совместна и имеет единственное решение.

Рассмотрим более содержательные задания:

Пример 14

Составить параметрические уравнения прямой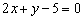

Решение: По условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку, принадлежащую данной прямой.

Найдём направляющий вектор: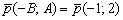

Теперь нужно найти какую-нибудь точку, принадлежащую прямой (подойдёт любая), в этих целях общее уравнение удобно переписать в виде уравнения с угловым коэффициентом: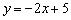

Напрашивается, конечно, точка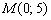

Составим параметрические уравнения прямой:

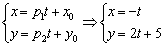
Ответ: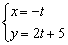

И напоследок небольшая творческая задача для самостоятельного решения.

Пример 15

Составить параметрические уравнения прямой, если известна принадлежащая ей точка 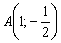и вектор нормали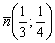

Задачу можно оформить не единственным способом. Одна из версий решения и ответ в конце урока.

Существуют другие, более экзотические способы задать прямую, но то, что уже рассмотрено, хватит за глаза и за уши. Следующая статья, которую я рекомендую, называется Простейшие задачи с прямой на плоскости. В ней рассматриваются вещи, которые позволят окончательно укрепить ваш геометрический фундамент.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: Найдём угловой коэффициент:

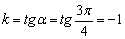
Уравнение прямой составим по точке 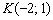и угловому коэффициенту :

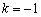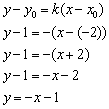
Ответ: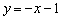

Пример 4: Решение: Уравнение прямой составим по формуле:

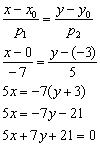
Ответ: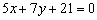

Пример 6: Решение: Используем формулу:

Ответ: 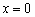(ось ординат)

Пример 8: Решение: Составим уравнение прямой по двум точкам:

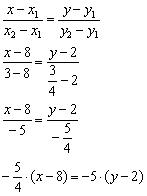
Умножаем обе части на –4:

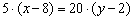
И делим на 5:

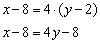
Ответ: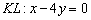

Пример 10: Решение: Используем формулу:

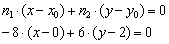
Сокращаем на –2:

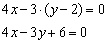
Направляющий вектор прямой: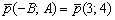
Ответ: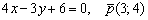

Пример 12:
а) Решение: Преобразуем уравнение:

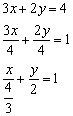
Таким образом:

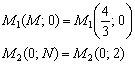
Ответ: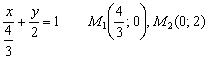

б) Решение: Преобразуем уравнение:

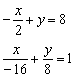
Таким образом:

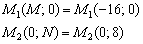
Ответ: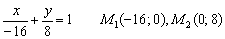

Пример 15: Решение: Сначала составим общее уравнение прямой по точке 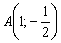и вектору нормали :

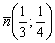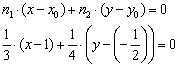
Умножаем на 12:

Умножаем ещё на 2, чтобы после раскрытия второй скобки избавиться от дроби:

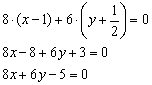
Направляющий вектор прямой: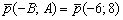
Параметрические уравнения прямой составим по точке 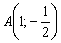и направляющему вектору :
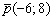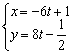
Ответ: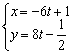

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Простейшие задачи с прямой на плоскости.
Взаимное расположение прямых. Угол между прямыми

Продолжаем рассматривать эти бесконечные-бесконечные прямые. На уроке Уравнение прямой на плоскости мы познакомились с основными видами уравнений, направляющим вектором прямой и её вектором нормали. Данная статья является логическим продолжением темы, и в ней будут разобраны следующие типовые задачи:

Как определить взаимное расположение двух прямых? Как построить прямую, параллельную данной? Как найти точку пересечения двух прямых? Как построить прямую, перпендикулярную данной? Как найти расстояние от точки до прямой? Как построить точку, симметричную относительно прямой? Как найти расстояние между двумя параллельными прямыми? Как найти угол между двумя прямыми?

О-о-о-о-о… ну и жесть, словно сам себе приговор зачитал =) Впрочем, потом релаксация поможет, тем более, сегодня купил подходящие аксессуары. Поэтому приступим к первому разделу, надеюсь, к концу статьи сохраню бодрое расположение духа.

Date: 2015-04-23; view: 1997; Нарушение авторских прав