Как составить уравнение прямой по двум точкам?

Если известны две точки 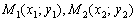, то уравнение прямой, проходящей через данные точки, можно составить по формуле:

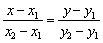
На самом деле это разновидность формулы 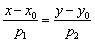и вот почему: если известны две точки 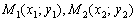, то вектор 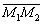будет направляющим вектором данной прямой. На уроке Векторы для чайников мы рассматривали простейшую задачу – как найти координаты вектора по двум точкам. Согласно данной задаче, координаты направляющего вектора: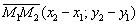

Примечание: точки можно «поменять ролями» и использовать формулу 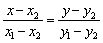. Такое решение будет равноценным.

Пример 7

Составить уравнение прямой по двум точкам .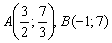

Решение: Используем формулу:

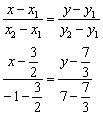
Причёсываем знаменатели:

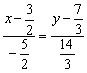
И перетасовываем колоду:

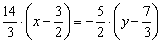
Именно сейчас удобно избавиться от дробных чисел. В данном случае нужно умножить обе части на 6:

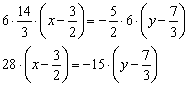
Раскрываем скобки и доводим уравнение до ума:

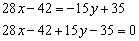
Ответ: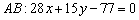

Проверка очевидна – координаты исходных точек должны удовлетворять полученному уравнению:

1) Подставим координаты точки :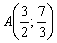

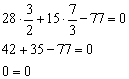
Верное равенство.

2) Подставим координаты точки :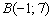

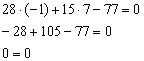
Верное равенство.

Вывод: уравнение прямой составлено правильно.

Если хотя бы одна из точек не удовлетворяет уравнению, ищите ошибку.

Стоит отметить, что графическая проверка в данном случае затруднительна, поскольку построить прямую 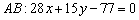и посмотреть, принадлежат ли ей точки 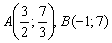, не так-то просто.

Отмечу ещё пару технических моментов решения. Возможно, в данной задаче выгоднее воспользоваться зеркальной формулой 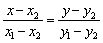и, по тем же точкам 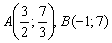составить уравнение:

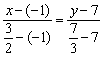
Таки дробей поменьше. Если хотите, можете довести решение до конца, в результате должно получиться то же самое уравнение.

Второй момент состоит в том, чтобы посмотреть на итоговый ответ и прикинуть, нельзя ли его ещё упростить? Например, если получилось уравнение 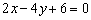, то здесь целесообразно сократить на двойку: 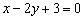– уравнение будет задавать ту же самую прямую. Впрочем, это уже тема разговора о взаимном расположении прямых.

Получив ответ 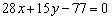в Примере 7, я на всякий случай, проверил, не делятся ли ВСЕ коэффициенты уравнения на 2, 3 или 7. Хотя, чаще всего подобные сокращения осуществляются ещё по ходу решения.

Пример 8

Составить уравнение прямой, проходящей через точки .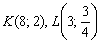

Это пример для самостоятельного решения, который как раз позволит лучше понять и отработать технику вычислений.

Аналогично предыдущему параграфу: если в формуле 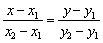один из знаменателей (координата направляющего вектора) обращается в ноль, то переписываем её в виде 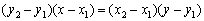. И снова заметьте, как неуклюже и запутанно она стала выглядеть. Не вижу особого смысла приводить практические примеры, поскольку такую задачу мы уже фактически прорешали (см. №№5,6).

Вектор нормали прямой (нормальный вектор)

Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), причём все векторы нормали прямой будут коллинеарными (сонаправленными или нет – без разницы).

Разборки с ними будут даже проще, чем с направляющими векторами:

Date: 2015-04-23; view: 1114; Нарушение авторских прав